\begin{equation} \label{Eqlegendre.2}
P_n (x) = \frac{1}{2^n} \sum_{k=0}^{\lfloor n/2 \rfloor} (-1)^k \binom{n}{k} \binom{2n-2k}{n} x^{n-2k} ,
\end{equation}
.
There are known also
\begin{equation} \label{Eqlegendre.3}
P_n^m (x) = P_{n,m} (x) = (-1)^m \left( 1 - x^2 \right)^{m/2} \frac{{\text d}^m}{{\text d} x^m} \, P_n (x) , \qquad m=0,1,2,\ldots , n, \quad x \in (-1,1) ,
\end{equation}
\begin{equation} \label{Eqlegendre.4}
\left( 1-x^2\right) y'' -2x\,y' + \left( \lambda - \frac{m^2}{1-x^2} \right) y =0 , \qquad x \in (-1, 1), \qquad y(\pm 1) < \infty , \qquad \lambda = n(n+1) .
\end{equation}
\begin{equation} \label{Eqlegendre.5}
\int_{-1}^1 P_n (x) \, P_m (x) \,{\text d} x = \begin{cases}
0 , & \ \mbox{for} \quad n\ne m,
\\
\frac{2}{2n+1} , & \ \mbox{for} \quad n = m. \end{cases}
\end{equation}
\begin{equation} \label{Eqlegendre.6}
\int_{-1}^1 P_n^m (x) \, P_k^m (x) \,{\text d} x = \begin{cases}
0 , & \ \mbox{for} \quad n\ne k,
\\
\frac{2}{2n+1} \cdot \frac{(n+m)!}{(n-m)!}, & \ \mbox{for} \quad n = k . \end{cases}
\end{equation}
w = 1/(1 - x ²):
\begin{equation} \label{Eqlegendre.7}
\int_{-1}^1 \frac{P_n^i (x) \, P_n^m (x)}{1 - x^2} \,{\text d} x = \begin{cases}
0 , & \ \mbox{for} \quad m\ne i,
\\
\frac{(n+m)!}{2(n-m)!}, & \ \mbox{for} \quad m = i \ne 0 , \\
\infty , & \ \mbox{for} \quad m = i =0. \end{cases}
\end{equation}
\[
\int_{-1}^1 P_n (x) \, P_m (x) \,{\text d} x = 0 \qquad\mbox{for} \quad n\ne m,
\]
any suitable function \( f (x) \) on the interval [-1,1] can be expanded into generalized Fourier--Legendre series:
\begin{equation} \label{Eqlegendre.8}
f(x) = \sum_{n\ge 0} c_n P_n (x) ,
\end{equation}
where the coefficients are
\begin{equation} \label{Eqlegendre.9}
c_n = \left( n + \frac{1}{2} \right) \int_{-1}^1 P_n (x) \, f(x) \,{\text d} x , \qquad n=0,1, \ldots ,
\end{equation}
because
\[
\int_{-1}^1 P_n^2 (x) \,{\text d} x = \frac{2}{2n+1} .
\]
Theorem 1:
If function
f satisfies the
Dirichlet conditions on the interval [−1, 1], then Legendre's series converges to
\[
\frac{f(x+0) + f(x-0)}{2} = \frac{f(x^{+}) + f(x^{-})}{2} = \sum_{n\ge 0} c_n P_n (x) ,
\]
where coefficients
c n are determined according to Eq.\eqref{Eqlegendre.9}.
As we will from the following examples, Fourier--Legandre series \eqref{Eqlegendre.8} exhibits the Gibbs phenomenon at the points of discontinuity. This phenomenon indicates that restoring a function from its Legendre series is an ill-posed problem. A convenient regularization is based on Cesàro summation
\begin{equation} \label{Eqlegendre.10}
(C.1)\,\sum_{n\ge 0} c_n P_n (x) = \lim_{N\to \infty} \sum_{n=0}^N \left( 1 - \frac{n}{N+1} \right) c_n P_n (x)
\end{equation}
The following theorem provides a simple sufficient condition for uniform convergence. There are known some less restrictive conditions that guarantee uniform convergence; however, we do not pursue this topic.
Theorem 2: f is continuously diffirentiable on the closed interval [−1, 1] (this condition is usually abbreviated as f ∈C ¹[−1, 1]), then the corresponding Legendre series \eqref{Eqlegendre.8} converges uniformly on this interval.
Suppose that f is an odd function on interval [−1, 1]. Since P n (x ) is odd when n is odd and P n (x ) is even when n is even, then the Legendre coefficients of f with even indices are all zero (c 2j = 0). The Legendre series of f contains only odd indexed polynomials. Similarly, if f is an even function, then its Legendre series contains only even indexed polynomials.
For any integer m , we can expand a smooth function into series with respect to associated Legendre functions
\begin{equation} \label{Eqlegendre.11}
f(x) = \sum_{n\ge m} a_n P_n^m (x) , \qquad a_n = \left( n + \frac{1}{2} \right) \frac{(n-m)!}{(n+m)!} \,\int_{-1}^1 f(x)\,P_n^m (x)\,{\text d}x , \quad n=0,1,2,\ldots .
\end{equation}
When derivative of f (x ) satisfies the condition
\[
\int_{-1}^1 \left( f'^2 (x) + \frac{m^2 f^2 (x)}{1-x^2} \right) {\text d}x < \infty ,
\]
then eigenfunction expansion \eqref{Eqlegendre.11} converges uniformely.
Example 1: Legendre series from generating function
Example 1: \( p = 2t/(1 + t^2 ) , \) we get
\[
\frac{1}{\sqrt{1 - px}} = \sqrt{1 + t^2} \sum_{n\ge 0} t^n P_n (x) .
\]
Upon its integration, we obtain
\[
\sqrt{1 - px} = \sqrt{1 + p} + \frac{p}{2} \sqrt{1+t^2} \left[ \frac{t}{3}\, P_0 (x) -1 - \sum_{n\ge 1} \left( \frac{t^{n-1}}{2n-1} - \frac{t^{n+1}}{2n+3} \right) P_n (x) \right] .
\]
In particular,
\[
\sqrt{1-x} = \frac{4}{3\sqrt{2}} \, P_0 (x) - \frac{4}{\sqrt{2}}\, \sum_{n\ge 1} \frac{1}{(2n-1)(2n+3)} \, P_n (x) , \qquad x \in (-1,1) .
\]
From this formula, we have
\[
\sqrt{1+x} = \frac{4}{3\sqrt{2}} \, P_0 (x) - \frac{4}{\sqrt{2}}\, \sum_{n\ge 1} \frac{(-1)^n}{(2n-1)(2n+3)} \, P_n (x) , \qquad x \in (-1,1) .
\]
Upon differentiation, we get
\[
\frac{1- x^2}{2\sqrt{1-x}} = \frac{4}{\sqrt{2}} \, \sum_{n\ge 1} \frac{n}{(2n-1)(2n+3)} \, P_{n-1} (x) -\frac{4x}{\sqrt{2}} \, \sum_{n\ge 1} \frac{n}{(2n-1)(2n+3)} \, P_{n} (x) , \qquad x \in (-1,1) .
\]
■
Example 2: Legendre series for arcsine function
Example 2:
\[
\frac{1}{\sqrt{1-x^2}} = \frac{\pi}{2}\,\sum_{n\ge 0} \left( 4n+1 \right) \left[ \frac{(2n-1)!!}{n!\,2^n} \right]^2 P_{2n} (x) , \qquad x \in (-1,1) .
\]
Note that we assume that (−1)!! = 1. Term by term integration yields
\[
\arcsin x = \frac{\pi}{2}\,\sum_{n\ge 0} \left[ \frac{(2n-1)!!}{n!\,2^n} \right]^2 P_{2n} (x) , \qquad x \in (-1,1) .
\]
■
Example 3: Fourier-Legendre series expansion of the Heaviside step function
Example 3: H(t) , defined on the finite interval [-1,1].
Its series expansion is written in the form
\[
H(t) = \sum_{n\ge 0} c_n \,P_n (t) , \qquad t \in [-1,1] .
\]
Substituting the explicit expressions for the Legendre polynomials, we get
\begin{align*}
c_n &= \frac{2n+1}{2} \, \int_{-1}^1 H(t)\, P_n (t)\,{\text d}t = \frac{2n+1}{2} \, \int_{0}^1 \, P_n (t)\,{\text d}t .
\end{align*}
Integrating by parts,
we find the explicit expressions for the coefficients:
\begin{align*}
c_n &= \frac{2n+1}{2} \,\frac{1}{2^n \,n!} \int_{0}^1 \frac{{\text d}^n}{{\text d} t^n} \left( t^2 -1 \right)^n {\text d}t = \frac{2n+1}{2^{n+1} n!} \, \left[ \frac{{\text d}^{n-1}}{{\text d} t^{n-1}} \left( t^2 -1 \right)^n \right]_{t=0}^{t=1} .
\\
&= \left\{
\begin{array}{ll}
0 , & \ \mbox{if $n$ is even} \\
(-1)^k \,\frac{(4k+3) \,(2k)!}{2^{2k+2}\,k! \,(k+1)!} , & \ \mbox{if $n = 2k+1$ is odd. }
\end{array}
\right.
\end{align*}
Thus, the Fourier--Legendre series expansion of the Heaviside function is given by
\[
H(t) = \frac{1}{2} + \sum_{k\ge 0} \, \frac{(-1)^k \,(4k+3) \,(2k)!}{2^{2k+2}\,k! \,(k+1)!} \, P_{2k+1} (x) .
\tag{3.1}
\]
Let us consider a partial sum of the series above:
\[
S_N (t) = \frac{1}{2} + \sum_{k= 0}^N (-1)^k c_{k+1} P_{2k+1} (x) , \qquad \mbox{with} \qquad c_{2k+1} = \frac{(4k+3) \,(2k)!}{2^{2k+2}\,k! \,(k+1)!}
\tag{3.2}
\]
Then we plot finite approximations with 5 and 20 terms:
legendre5 =
1/2 + Sum[(-1)^k *(4*k + 3)*
Factorial[2*k]/2^(2*k + 2)/Factorial[k + 1]/Factorial[k] *
LegendreP[2*k + 1, t], {k, 0, 5}];
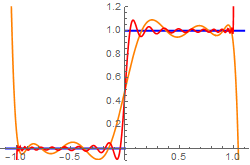
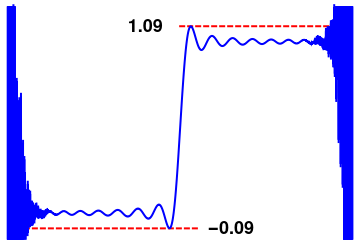
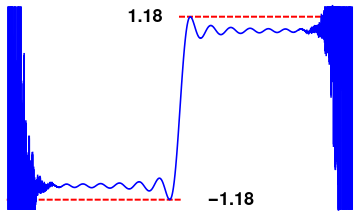
The graph clearly indicates on an existence of the Gibbs phenomenon at the origin. To investigate its presence, we increase the number of terms in the partial sum (3.2). Upon plotting with N = 22 terms, we observe divergence of Legendre series (3.1) at end points x = ±1. In order to eliminate the Gibbs phenomenon, we use Cesàro regularization
\[
C_N (t) = \frac{1}{2} + \sum_{k= 0}^N (-1)^k c_{k+1} \left( 1 - \frac{2k+1}{2N+2} \right) P_{2k+1} (x) , \qquad \mbox{with} \qquad c_{2k+1} = \frac{(4k+3) \,(2k)!}{2^{2k+2}\,k! \,(k+1)!}
\tag{3.3}
\]
legendre24 =
1/2 + Sum[(-1)^k*
N[(4*k + 3)*
Factorial[2*k]/2^(2*k + 2)/Factorial[k + 1]/Factorial[k]]*
LegendreP[2*k + 1, t], {k, 0, 24}];
Legendre approximation with N = 24.
Cesàro approximation with N = 24.
■
Example 4: Shifted Heaviside function
Example 4:
\[
H(t-a) = \begin{cases}
0, & \ \mbox{ for} \quad -1 < x < a , \\
1, & \ \mbox{ for} \quad -1 < x > a ,
\end{cases}
\]
can be expanded into Fourier--Legandre series \eqref{Eqlegendre.8}:
\[
H(t-a) = \frac{1-a}{2} + \frac{1}{2} \sum_{n\ge 1} \left[ P_{n-1} (a) - P_{n+1} (a) \right] P_n (x) .
\]
■
Example 5: Fourier--Legendre series expansion of the signum step function
Example 5:
\[
\sum_{n\ge 0} c_n P_n (x) = \mbox{sign}(x) = \begin{cases}
\phantom{-}1, & \ \mbox{ if} \quad 0 < x < 1, \\
-1, & \ \mbox{ if} \quad -1 < x < 0.
\end{cases}
\tag{6.1}
\]
Since signum function is an odd function, its Legendre series contains only terms with odd indices:
\[
\mbox{sign}(x) = \sum_{k\ge 0} c_{2k+1} P_{2k+1} (x) .
\tag{6.2}
\]
Using an integration formula
\[
\int_{-1}^x P_n (t) \,{\text d}t = \frac{P_{n+1} (x) - P_{n-1} (x)}{2n+1} ,
\]
we find the explicit expressions for the coefficients:
\[
c_n = \frac{2n+1}{2}\,\int_{-1}^i \mbox{sign}(x)\, P_n (x) \,{\text d}x = P_{n-1} (0) - P_{n+1} (0) , \qquad n=1,2,\ldots ,
\]
where
\( P_{2k+1} (0) =0 \) and formulas for even indices was given previously:
\[
P_{2k} (0) = (-1)^k \frac{(2k)!}{2^{2k} (k!)^2} .
\]
In particular, we have
\[
\mbox{sign}(x) = \sum_{k\ge 0} \left( \frac{(-1)^k (4k+3) \left( 2k \right)!}{2^{2k+1} k! \left( k+1 \right)!} \right) P_{2k+1} (x) \qquad \mbox{for} \quad -1 < x < 1 .
\tag{6.3}
\]
We now use
Mathematica to calculate the coefficients up to arbitrary
n , starting with
n = 1 .
Module[{i}, coef = {};
Do[coef =
Append[coef, (LegendreP[i - 1, 0] - LegendreP[i + 1, 0])], {i, 1,
30}]]
The
n th coefficient is then given by
coef[[n]] . We sample a few values:
coef[[21]]
Out[34]= 180557/524288
coef[[22]]
Out[35]= 0
All the even coefficients are zero.
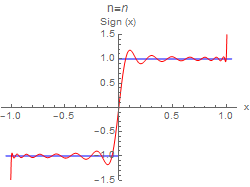
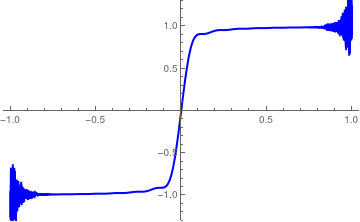
Now we define the m th partial sum, and then a graph of the m th partial sum, along with the original function. Because the coefficient of \( P_{0} (x)=1 \) is zero, we may start the sum over n with the n = 1 term. The given signum function is shown in blue and the partial sums in red.
legsum[m_, x_] :=
Module[{i}, Sum[N[coef[[i]]]*LegendreP[i, x], {i, 1, m}]]
You may want to construct a sequence of partial sums which may be animated to see the convergence:
DynamicModule[{mangraph, i},
Do[mangraph[i] = legraph[i], {i, 1, 55, 2}];
Manipulate[mangraph[i], {i, 1, 51, 2}]]
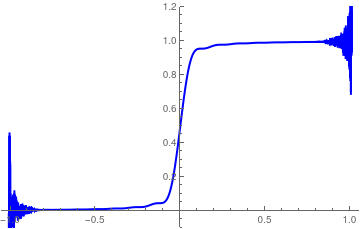
You can use the slider to move through the graphs, and also to display a movie of the graphs. When you do this, you will see the familiar Gibbs overshoot/undershoot at the discontinuity. It is also observed a struggle to converge at the endpoints.
Module[{a}, coef = {};
Do[coef =
Append[coef, (LegendreP[x - 1, 0] - LegendreP[x + 1, 0])], {x, 1,
100}]]
legsum[m_, x_] :=
Module[{a}, -Sum[N[coef[[a]]]*LegendreP[a, x], {a, 1, m}]]
leg[x_] = Piecewise[{{1, -1 <= x < 0}, {-1, 0 < x <= 1}}];
legraph[m_] :=
Plot[{leg[x], legsum[m, x]}, {x, -1, 1}, PlotRange -> {-1.5, 1.5},
PlotStyle -> {{RGBColor[0, 0, 1],
Thickness[0.005]}, {RGBColor[1, 0, 0], Thickness[0.005]}}]
legraph[10]
legraph[100]
Numerical experiments show that the legendre series (6.3) exhibits the Gibbs phenomenon at the origin---the point of discontinuity. The series also diverges at endpoints x = ±1. To elinante unwanted overshoots and undershoots at the origin, we consider Cesàro approximation
\[
C_N (x) = \sum_{k= 0}^N \left( \frac{(-1)^k (4k+3) \left( 2k \right)!}{2^{2k+1} k! \left( k+1 \right)!} \right) \left( 1 - \frac{k}{N+1} \right) P_{2k+1} (x) \qquad \mbox{for} \quad -1 < x < 1 .
\tag{6.4}
\]
sign25 = Sum[(-1)^k*
N[(4*k + 3)*
Factorial[2*k]/2^(2*k + 1)/Factorial[k + 1]/Factorial[k]]*
LegendreP[2*k + 1, t], {k, 0, 25}];
Legendre approximation with N = 25.
Cesàro approximation with N = 25.
■
Example 6: Fourier--Legendre series expansion of the delta function
Example 6:
\[
\delta (x-a) = \sum_{k\ge 0} \left( k + \frac{1}{2} \right) P_k (x)\, P_k (a) .
\]
or
\[
\delta (x-a) = \frac{1}{2} \sum_{k\ge 0} \left( 2k+1 \right) P_k (x)\, P_k (a) .
\]
So the partial sums
\[
\delta_N (x-a) = \frac{1}{2} \sum_{k= 0}^{N} \left( 2k+1 \right) P_k (x)\, P_k (a) \qquad \mbox{for} \quad |x| < 1,
\]
have the property:
\[
\lim_{N\to \infty} \int_{-1}^1 {\text d}x \, \delta_N (x-a) \,f(x) = f(a) .
\]
■
Example 7: Legendre series for piecewise linear functions
Example 7:
\[
f(x) = |x| \qquad\mbox{and} \qquad g(x) = \begin{cases}
x, & \ \mbox{for} \quad x \ge 0, \\
0, & \ \mbox{for} \quad x \le 0.
\end{cases}
\]
The corresponding Fourier--Legendre coefficients can be evaluated based on the formulas:
\[
\int_{-1}^1 P_n (x)\,{\text d}x = 0 \qquad \mbox{and} \qquad \int_{-1}^a P_n (x)\,{\text d}x = \frac{1}{2n+1} \left[ P_{n+1} (a) - P_{n-1} (a) \right] .
\]
■
Example 8: Piecewise differentiable function
Example 8:
\[
f(x) = \begin{cases}
x^2 , & \mbox{ when} \quad x \ge 0 , \\
0, & \mbox{ when} \quad x \le 0 .
\end{cases}
\tag{8.1}
\]
Expanding this function into Legendre series, we get
\[
f(x) = \sum_{n\ge 0} c_n P_n (x) , \qquad c_n = \left( n + \frac{1}{2} \right) \int_0^1 x^2 P_n (x) \,{\text d} x .
\tag{8.2}
\]
Using formula
\[
P'_{n+1} (x) - P'_{n-1} (x) = \left( 2n+1 \right) P_n (x) ,
\tag{8.3}
\]
we integrate by parts
\[
c_n = \frac{1}{2}\, \int_0^1 x^2 \frac{\text d}{{\text d}x} \left( P_{n+1} (x) - P_{n-1} (x) \right) {\text d} x = \frac{1}{2} \left( P_{n+1} (1) - P_{n-1} (1) \right) - \int_0^1 x \left( P_{n+1} (x) - P_{n-1} (x) \right) {\text d} x .
\]
Since
P n (1) = 1, we get
\[
c_n = -\frac{1}{2n+3}\, \int_0^1 x \left( P'_{n+2} (x) - P'_{n} (x) \right) {\text d} x + \frac{1}{2n-1}\, \int_0^1 x \left( P'_{n} (x) - P'_{n-2} (x) \right) {\text d} x
\]
Next integration by [arts yields
\[
c_n = \frac{1}{2n+3}\, \int_0^1 \left( P_{n+2} (x) - P_{n} (x) \right) {\text d} x - \frac{1}{2n-1}\, \int_0^1 \left( P_{n} (x) - P_{n-2} (x) \right) {\text d} x
\]
Again, using formular (8.3), we simplify
\[
c_n = \left. \frac{1}{2n+3}\,\frac{1}{2n+5}\left( P_{n+3} (x) - P_{n+1} (x) \right) \right\vert_{x=0}^{x=1} - \left. \frac{1}{2n+3}\,\frac{1}{2n+1}\left( P_{n+1} (x) - P_{n-1} (x) \right) \right\vert_{x=0}^{x=1} - \left. \frac{1}{2n-1}\,\frac{1}{2n+1}\left( P_{n+1} (x) - P_{n-1} (x) \right) \right\vert_{x=0}^{x=1} + \left. \frac{1}{2n-1}\,\frac{1}{2n-3}\left( P_{n-1} (x) - P_{n-3} (x) \right) \right\vert_{x=0}^{x=1} .
\]
It is known that
\[
P_{2k+1} (0) = 0, \qquad P_{2k} (0) = (-1)^k \frac{(2k-1)!!}{(2k)!!} ,
\]
so the value of
c n depends on the parity of
n . If
n = 2
k , even, all coefficientsa are zeroes for
n > 3. When
n = 2
k +1, odd, we have
\[
c_{2k+1} = - \frac{(-1)^k}{\left( 2k+6 \right)\left( 2k+4 \right)} \cdot \frac{(2k+3)!!}{(2k+4)!!}
\]
■
Return to Mathematica page main page (APMA0340) Part 1 Matrix Algebra Part 2 Linear Systems of Ordinary Differential Equations Part 3 Non-linear Systems of Ordinary Differential Equations Part 4 Numerical Methods Part 5 Fourier Series Part 6 Partial Differential EquationsPart 7 Special Functions