Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to the main page for the fourth course APMA0360
Return to Part I of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Preface
This section provides the general introduction to vector theory including inner and outer products. It also serves as a tutorial for operations with vectors using Mathematica. Although vectors have physical meaning in real life, they can be uniquely identified with ordered tuples of real (or complex numbers). The latter is heavily used in computers to store data as arrays or lists.
How to define vectors
As you know from calculus, a vector in the three dimensional space is a quantity that has both magnitude and direction. Recall that in contrast to a vector, a scalar has only a magnitude. It is commonly represented by a directed line segment whose length is the magnitude and with an arrow indicating the direction in space: \( \overleftarrow{v} \) or \( \overrightarrow{v} . \) However, we denote vectors using boldface as in a. The magnitude of a vector is called the norm or length, and it is denoted by double vertical lines, as ∥a∥. The direction of the vector is from its tail to its head. Two geometric vectors are equal if they have the same magnitude and direction. This means that we are allowed to translate a vector to a new location (without rotating it); for instance, starting at the origin.
The main reason why vectors are so useful and popular is that we can do operations with them similarly to ordinary algebra. Namely, there is an internal operation on vectors called addition together with its negation---subtraction. So two vectors can be added or subtracted. Besides these two internal arithmetic operations, there is another outer operation that admits multiplication of a vector by a scalar (real or complex numbers). It is also assumed that there exists a unique zero vector (of zero magnitude and no direction), which can be added/subtracted from any vector without changing the outcome. The zero vector is not the number zero, but it is obtained upon multiplication of any vector by scalar zero. When discussing vectors geometrically, we assume that scalars are real numbers.
Addition of vectors
For two given vectors a and b, their sum a+b is determined as follows. We translate the vector b until its tail coincides with the head of a. (Recall such translation does not change a vector.) Then, the directed line segment from the tail of a to the head of b is the vector a+b.

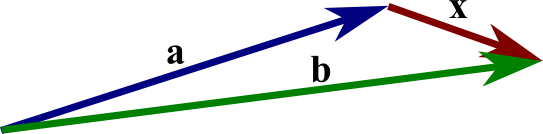
-
a + b = b + a (commutative law);
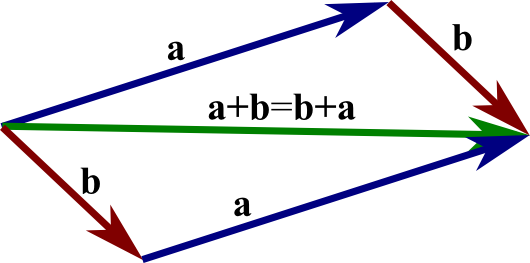
Commutative law - (a + b) + c = a + (b + c) (associative law);
- There is a vector 0 such that b + 0 = b (additive identity);
- For any vector a, there is a vector −a such that a + (−a) = 0 (Additive inverse).
Scalar multiplication
Given a vector a and a real number (scalar) λ, we can form the vector λa as follows. If λ is positive, then λa is the vector whose direction is the same as the direction of a and whose length is λ times the length of a. In this case, multiplication by λ simply stretches (if λ>1) or compresses (if 0<λ<1) the vector a. If, on the other hand, λ is negative, then we have to take the opposite of a before stretching or compressing it. In other words, the vector λa points in the opposite direction of a, and the length of λa is |λ| times the length of a. No matter the sign of λ, we observe that the magnitude of λa is |λ| times the magnitude of a: ∥λa∥ = |λ| ∥a∥. Scalar multiplications satisfies many of the same properties as the usual multiplication.- λ(a + b) = λa + λb (distributive law, for vectors)
- (λ + β)a = λa + βb (distributive law for scalars);
- 1·a = a;
- (−1)·a = −a;
- 0·a = 0.
Generalizing well-known examples of vectors (velocity and force) in physics and engineering, mathematicians introduced abstract object called vectors. So vectors are objects that can be added/subtracted and multiplied by scalars. These two operations (internal addition and external scalar multiplication) are assumed to satisfy natural conditions described above. A set of vectors is said to form a vector space (also called a linear space), if any vectors from it can be added/subtracted and multiplied by scalars, subject to regular properties of addition and multiplication. Wind, for example, has both a speed and a direction and, hence, is conveniently expressed as a vector. The same can be said of moving objects, momentum, forces, electromagnetic fields, and weight. (Weight is the force produced by the acceleration of gravity acting on a mass.)
The first thing we need to know is how to define a vector so it will be clear to everyone. Today more than ever, information technologies are an integral part of our everyday lives. That is why we need a tool to model vectors on computers. One of the common ways to do this is to introduce a system of coordinates, either Cartesian or any other. In engineering, we traditionally use the Cartesian coordinate system that specifies any point with a string of digits. Each coordinate measures a distance from a point to its perpendicular projections onto the mutually perpendicular hyperplanes.
Let us start with our familiar three dimensional space in which the Cartesian coordinate system consists of an ordered triplet of lines (the axes) that go through a common point (the origin), and are pair-wise perpendicular; it also includes an orientation for each axis and a single unit of length for all three axes. Every point is assigned distances to three mutually perpendicular planes, called coordinate planes (such that the pair x and y axes define the z-plane, x and z axes define the y-plane, etc.). The reverse construction determines the point given its three coordinates. Each pair of axes defines a coordinate plane. These planes divide space into eight trihedra, called octants. The coordinates are usually written as three numbers (or algebraic formulas) surrounded by parentheses or brackets and separated by commas, as in (-2.1,0.5,7) or [-2.1,0.5,7]. Thus, the origin has coordinates (0,0,0), and the unit points on the three axes are (1,0,0), (0,1,0), and (0,0,1).
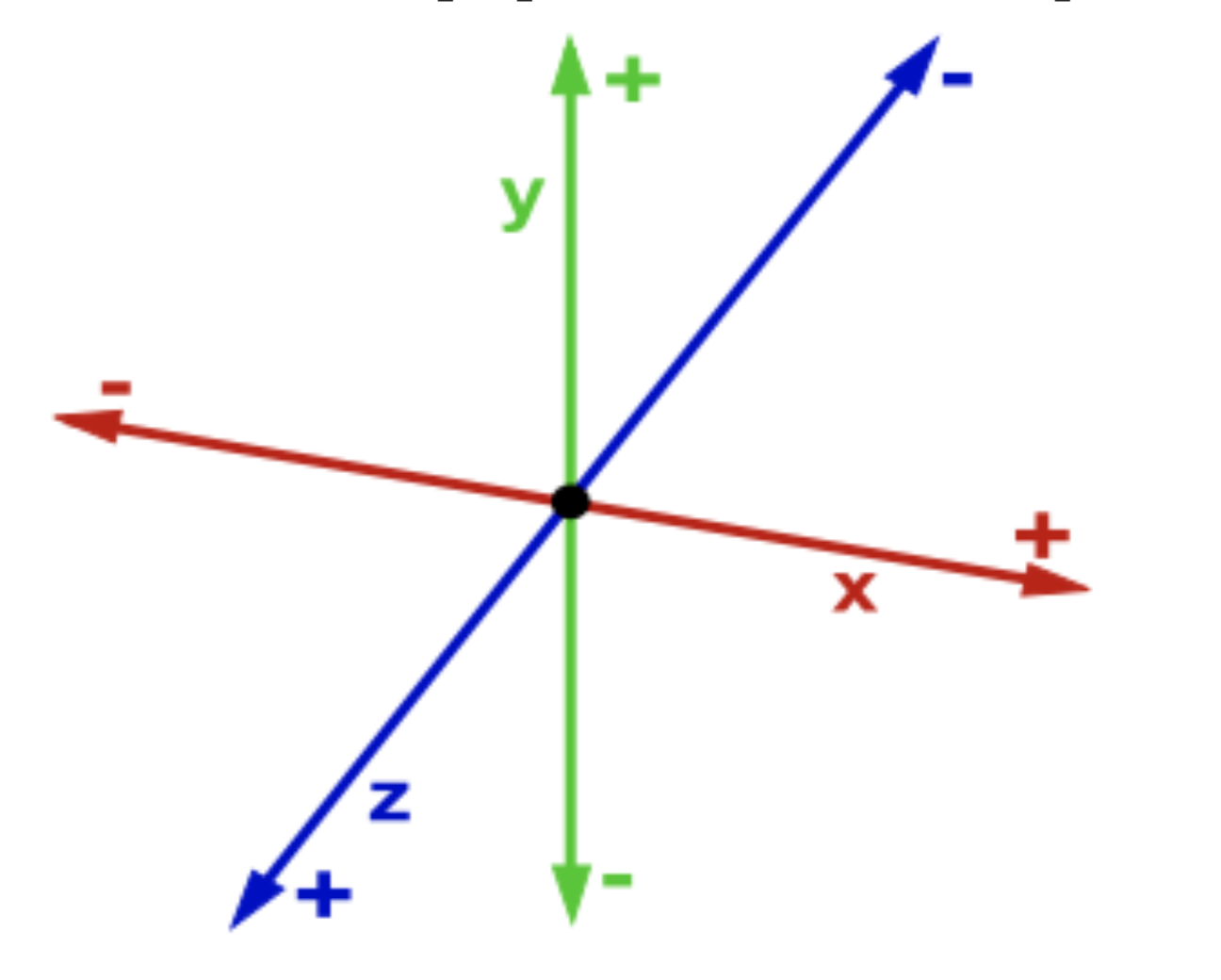
There are no universal names for the coordinates in the three axes. However, the horizontal axis is traditionally called abscissa borrowed from New Latin (short for linear abscissa, literally, "cut-off line"), and usually denoted by x. The next axis is called ordinate, which came from New Latin (linea), literally, line applied in an orderly manner; we will usually label it by y. The last axis is called applicate and usually denoted by z. Correspondingly, the unit vectors are denoted by i (abscissa), j (ordinate), and k (applicate), called the basis. Once rectangular coordinates are set up, any vector can be expanded through these unit vectors. In the three dimensional case, every vector can be expanded as \( {\bf v} = v_1 {\bf i} + v_2 {\bf j} + v_3 {\bf k} ,\) where \( v_1, v_2 , v_3 \) are called the coordinates of the vector v. Coordinates are always specified relative to an ordered basis. When a basis has been chosen, a vector can be expanded with respect to the basis vectors and it can be identified with an ordered n-tuple of n real (or complex) numbers or coordinates. The set of all real (or complex) ordered numbers is denoted by ℝn (or ℂn). In general, a vector in infinite dimensional space is identified by an infinite sequence of numbers. Finite dimensional coordinate vectors can be represented by either a column vector (which is usually the case) or a row vector. We will denote column-vectors by lower case letters in bold font, and row-vectors by lower case letters with a superimposed arrow. Because of the way the Wolfram Language uses lists to represent vectors, Mathematica does not distinguish column vectors from row vectors, unless the user specifies which one is defined. One can define vectors using Mathematica commands: List, Table, Array, or curly brackets.
In mathematics and applications, it is a custom to distinguish column vectors
The concept of a vector space (also a linear space) has been defined abstractly in mathematics. Historically, the first ideas leading to vector spaces can be traced back as far as the 17th century; however, the idea crystallized with the work of the German mathematician Hermann Günther Grassmann (1809--1877), who published a paper in 1862. A vector space is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars, the result producing more vectors in this collection. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally scalars in any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms (they can be found on the web page).
Vectors in Mathematica are built, manipulated and accessed
similarly to matrices (see next section). However,
as simple lists (“one-dimensional,” not “two-dimensional” such as matrices
that look more tabular), they are easier to construct and manipulate. They
will be enclosed in brackets ( [,] ) which allows us to distinguish a
vector from a matrix with just one row, if we look carefully. The
number of “slots” in a vector is not referred to in Mathematica as
rows or columns, but rather by “size.”
In Mathematica, defining vectors and matrices is done by typing every row in curly brackets:
A column vector can be constructed from curly brackets shown here { }. A comma delineates each row. The output, however, may not look like a column vector. To fix this you must call //MatrixForm on your variable representation of a row vector.
MatrixForm[u]
1
2
3
4
Constructing a row vector is very similar to constructing a column vector, except two sets of curly brackets are used. Again the output looks like a row vector and so //MatrixForm must be called to put the row vector in the format that you more familiar with:
MatrixForm[n]
{ 1 2 3 4 }
a // TraditionalForm
b // MatrixForm
a = {1, 0, 2};
A.a
Take[Etotal[{x, y, 0}, 2]];
|
Another version of the same plot:
charge[q_, {x0_, y0_, z0_}][x_, y_, z_] :=
q/((x - x0)^2 + (y - y0)^2 + (z - z0)^2)^(3/2) {x - x0, y - y0,
z - z0};
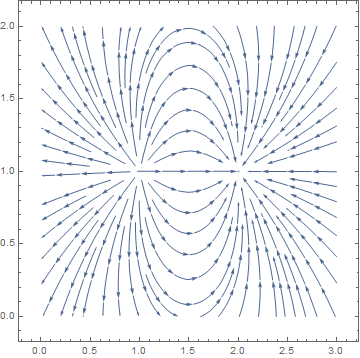
projector[{x_, y_, z_}] := {x, y} VectorPlot[ projector[ charge[1, {0, 4, 0}][x, y, 0] + charge[-1, {0, -4, 0}][x, y, 0]], {x, -10, 10}, {y, -10, 10}]; StreamPlot[ projector[ charge[1, {-2, 0, 0}][x, y, 0] + charge[-1, {2, 0, 0}][x, y, 0]], {x, -5, 5}, {y, -5, 5}] |
|
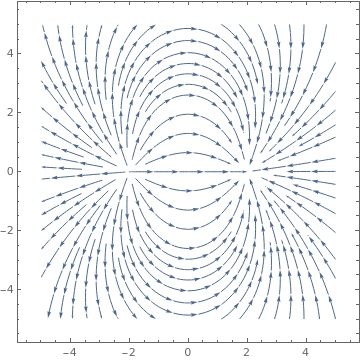
| Electric field potential of a dipole. | Mathematica code |
First, we define the Coulomb fields at the origin using "Ec" in the code below
|
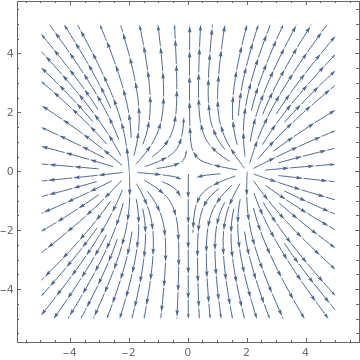
A completely different vector field is obtained when we add two equal charges:
Ec[x_, y_] := {x/(x^2 + y^2)^(3/2), y/(x^2 + y^2)^(3/2)};
StreamPlot[Ec[x + 2, y] + Ec[x - 2, y], {x, -5, 5}, {y, -5, 5}] |
|
| Electric field potential of two equal charges. | Mathematica code |
We can visualize vector fields in 3-dimensional space. ■
Both a vector and a matrix can be multiplied by a scalar; with the operation being *. Matrices and vectors can be added or subtracted only when their dimensions are the same.
(1) S is a linearly independent subset of V if and only if no vector in S can be expressed as a linear combination of the other vectors in S.
(2) S is a linearly dependent subset of V if and only if some vector v in S can be expressed as a linear combination of the other vectors in S.
- S spans V;
- S is linearly independent. ▣
Vector products
Mathematica has three multiplication commands for vectors: the dot (or inner) and outer products (for arbitrary vectors), and the cross product (for three dimensional vectors).
For three dimensional vectors \( {\bf a} = a_1 \,{\bf i} + a_2 \,{\bf j} + a_3 \,{\bf k} = \left[ a_1 , a_2 , a_3 \right] \) and \( {\bf b} = b_1 \,{\bf i} + b_2 \,{\bf j} + b_3 \,{\bf k} = \left[ b_1 , b_2 , b_3 \right] \) , it is possible to define special multiplication, called the cross-product:
The cross product can be done on two vectors. It is important to note that the cross product is an operation that is only functional in three dimensions. The operation can be computed using the Cross[vector 1, vector 2] operation or by generating a cross product operator between two vectors by pressing [Esc] cross [Esc]. ([Esc] refers to the escape button)
The dot product of two vectors of the same size \( {\bf x} = \left[ x_1 , x_2 , \ldots , x_n \right] \) and \( {\bf y} = \left[ y_1 , y_2 , \ldots , y_n \right] \) (regardless of whether they are columns or rows because Mathematica does not distinguish rows from columns) is the number, denoted either by \( {\bf x} \cdot {\bf y} \) or \( \left\langle {\bf x} , {\bf y} \right\rangle ,\)
when entries are complex. Here \( \overline{\bf x} = \overline{a + {\bf j}\, b} = a - {\bf j}\,b \) is a complex conjugate of a complex number x = a + jb.
The dot product of any two vectors of the same dimension can be done with the dot operation given as Dot[vector 1, vector 2] or with use of a period “. “ .
An outer product is the tensor product of two coordinate vectors \( {\bf u} = \left[ u_1 , u_2 , \ldots , u_m \right] \) and \( {\bf v} = \left[ v_1 , v_2 , \ldots , v_n \right] , \) denoted \( {\bf u} \otimes {\bf v} , \) is an m-by-n matrix W of rank 1 such that its coordinates satisfy \( w_{i,j} = u_i v_j . \) The outer product \( {\bf u} \otimes {\bf v} , \) is equivalent to a matrix multiplication \( {\bf u} \, {\bf v}^{\ast} , \) (or \( {\bf u} \, {\bf v}^{\mathrm T} , \) if vectors are real) provided that u is represented as a column \( m \times 1 \) vector, and v as a column \( n \times 1 \) vector. Here \( {\bf v}^{\ast} = \overline{{\bf v}^{\mathrm T}} . \)
MatrixRank[%]
An inner product of two vectors of the same size, usually denoted by \( \left\langle {\bf x} , {\bf y} \right\rangle ,\) is a generalization of the dot product if it satisfies the following properties:
- \( \left\langle {\bf v}+{\bf u} , {\bf w} \right\rangle = \left\langle {\bf v} , {\bf w} \right\rangle + \left\langle {\bf u} , {\bf w} \right\rangle . \)
- \( \left\langle {\bf v} , \alpha {\bf u} \right\rangle = \alpha \left\langle {\bf v} , {\bf u} \right\rangle \) for any scalar α.
- \( \left\langle {\bf v} , {\bf u} \right\rangle = \overline{\left\langle {\bf u} , {\bf v} \right\rangle} , \) where overline means complex conjugate.
- \( \left\langle {\bf v} , {\bf v} \right\rangle \ge 0 , \) and equal if and only if \( {\bf v} = {\bf 0} . \)
The fourth condition in the list above is known as the positive-definite condition. A vector space together with the inner product is called an inner product space. Every inner product space is a metric space. The metric or norm is given by
The invention of Cartesian coordinates in 1649 by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra.
Vector norms
- Positivity: ‖v‖ ≥ 0, ‖v‖ = 0 iff v = 0.
- Homogeneity: ‖kv‖ = |k| ‖v‖ for arbitrary scalar k.
- Triangle inequality: ‖v + u‖ ≤ ‖u‖ + ‖v‖.
-
For every x = [x1, x2, … , xn] ∈ V, we have the 1-norm:
\[ \| {\bf x}\|_1 = \sum_{k=1}^n | x_k | = |x_1 | + |x_2 | + \cdots + |x_n |. \]It is also called the Taxicab norm or Manhattan norm.
-
The Euclidean norm or ℓ²-norm is
\[ \| {\bf x}\|_2 = \left( \sum_{k=1}^n x_k^2 \right)^{1/2} = \left( x_1^2 + x_2^2 + \cdots + x_n^2 \right)^{1/2} . \]
-
The Chebyshev norm or sup-norm ‖v‖∞, is defined such that
\[ \| {\bf x}\|_{\infty} = \max_{1 \le k \le n} \left\{ | x_k | \right\} . \]
-
The ℓp-norm (for p≥1)
\[ \| {\bf x}\|_p = \left( \sum_{k=1}^n x_k^p \right)^{1/p} = \left( x_1^p + x_2^p + \cdots + x_n^p \right)^{1/p} . \]
- \( \displaystyle \| {\bf x} \|_{\infty} \le \| {\bf x} \|_{1} \le n\,\| {\bf x} \|_{\infty} , \)
- \( \displaystyle \| {\bf x} \|_{\infty} \le \| {\bf x} \|_{2} \le \sqrt{n}\,\| {\bf x} \|_{\infty} , \)
- \( \displaystyle \| {\bf x} \|_{2} \le \| {\bf x} \|_{1} \le \sqrt{n}\,\| {\bf x} \|_{2} .\)
With dot product, we can assign a length of a vector, which is also called the Euclidean norm or 2-norm:
For any norm, the Cauchy--Bunyakovsky--Schwarz (or simply CBS) inequality holds:
 |
 |
 |
||
|---|---|---|---|---|
| Augustin-Louis Cauchy | Viktor Yakovlevich Bunyakovsky | Hermann Amandus Schwarz |
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions