Preface
This tutorial was made solely for the purpose of education and it was designed for students taking Applied Math 0340. It is primarily for students who have some experience using Mathematica. If you have never used Mathematica before and would like to learn more of the basics for this computer algebra system, it is strongly recommended looking at the APMA 0330 tutorial. As a friendly reminder, don't forget to clear variables in use and/or the kernel. The Mathematica commands in this tutorial are all written in bold black font, while Mathematica output is in normal font.
Finally, you can copy and paste all commands into your Mathematica notebook, change the parameters, and run them because the tutorial is under the terms of the GNU General Public License (GPL). You, as the user, are free to use the scripts for your needs to learn the Mathematica program, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. The tutorial accompanies the textbook Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043
Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part VI of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Numerical Solutions to Wave Equation
Consider the wave equation
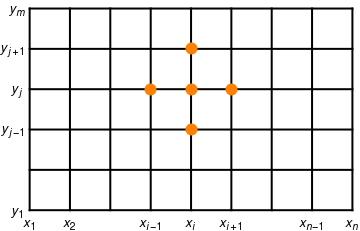
We partition the rectangle \( R = \left\{ (x,t)\, : \, 0 \le x \le \ell , \ 0 \le t \le b \right\} \) into a grid consisting of n-1 by m-1 rectangles with sides \( \Delta x = h \) and Δt = k, as shown in Figure.
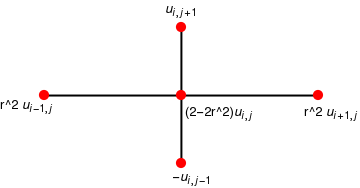
The central-difference formulas for approximating utt(x,t) and uxx(x,t) are
l1 = Graphics[{Thick, Line[{{0, -2}, {0, 2}}]}];
d0 = Graphics[{Red, Disk[{0, 0}, 0.15]}];
d1 = Graphics[{Red, Disk[{4, 0}, 0.15]}];
d2 = Graphics[{Red, Disk[{-4, 0}, 0.15]}];
d3 = Graphics[{Red, Disk[{0, 2}, 0.15]}];
d4 = Graphics[{Red, Disk[{0, -2}, 0.15]}];
r1 = Graphics[ Text[Style["(2-2r^2)\!\(\*SubscriptBox[\(u\), \(i,j\)]\)", Medium], {1.1, -0.5}]];
r2 = Graphics[Text[ Style["r^2 \!\(\*SubscriptBox[\(u\), \(i+1,j\)]\)", Medium], {4.4, -0.5}]];
r3 = Graphics[Text[ Style["r^2 \!\(\*SubscriptBox[\(u\), \(i-1,j\)]\)", Medium], {-4.5, -0.3}]];
r4 = Graphics[Text[ Style["\!\(\*SubscriptBox[\(u\), \(i,j+1\)]\)", Medium], {0, 2.5}]];
r5 = Graphics[Text[ Style["-\!\(\*SubscriptBox[\(u\), \(i,j-1\)]\)", Medium], {0.3, -2.4}]];
Show[l0, l1, d0, d1, d2, d3, d4, r1, r2, r3, r4, r5]
Two starting rows of values corresponding to j = 1 and j = 2 must be supplied in order to use the explicit recurrence formula. Since the second row is not usually given, the boundary function g(x) is used to help produce starting approximations in the second row. Fix x = xi at the boundary and apply Taylor's formula of order 1 for expanding u(x,t) about (xi, 0). The value at this point satisfies
Often, the boundary function f(x) has a second derivative over the interval. In this case, we have \( u_{xx} (x,0) = f'' (x) , \) and it is beneficial to use the Taylor formula of order 2 to help construct the second row. To do this, we go back to the wave equation and use the relationship between the second order partial derivatives to obtain
II. Two Exact Rows given
the accuracy of the numerical approximations depends on the truncation errors in the formulas used to convert the partial differential equation into a difference equation. Although it is unlikely to know values of the exact solution for the second row of the grid, if such knowledge were available, using the increment k = ch along the t-axis will generate an exact solution at all the other points throughout the grid.
Note: Theorem does not guarantee that the numerical solutions are exact when numerical calculations based on
Program (Finite-difference method for the wave equation): to approximate the solution of \( u_{tt} = c^2 u_{xx} \) over \( R = \{\,(x,t) \,:\, 0 \le x \le \ell , \ 0 \le t \le b \) with u(x,0) = f(x), ut(x,0) = g(x), for 0 ≤ x ≤ ℓ, and u(0,t) = 0, u(ℓ,t) = 0, for 0 ≤ t ≤ b.
function U=wave(f,g,a,b,c,n,m)
% Input -- f=u(x,0) as a string 'f'
% -- g=ut(x,0) as a string 'g'
% -- a and b right end points of [0,a] and [0,b]
% -- c=the speed constant in wave equation
% -- n and m number of grid points over [0,a] and [0,b]
% Output -- U solution matrix;
% Initialize parameters and U
h=a/(n-1);
k=b/(m-1);
r=c*k/h;
r2=r^2;
r22=r^2/2;
s1=1-r^2;
s2=2-2*r^2;
U=zeros(n,m);
% Compute first and second rows
for i=2:n-1
U(i,1)=feval(f,h*(i-1));
U(i,2)=s1*feval(f,h*(i-1))+k*feval(g,h*(i-1))+r22*(feval(f,h*i) + feval(f,h*(i-2)));
end
% Compute remaining rows of U
for j=3:m,
for i=2:(n-1),
U(i,j) = s2*U(i,j-1)+r2*(U(i-1,j-1)+U(i+1,j-1))-u(i,j-2);
end
end
U=U';
Example: Consider the initial boundary value problem modeling a vibrating string:
- Abdulkadir, Y. (2015) Comparison of Finite Difference Schemes for the Wave Equation Based on Dispersion. Journal of Applied Mathematics and Physics, 3, 1544-1562. doi: 10.4236/jamp.2015.311179.
- Bilbao, S. and Smith, J., Finite Difference Schemes and Digital Waveguide Networks for the Wave Equation: Stability, Passivity, and Numerical Dispersion, IEEE Transactions on Speech and Audio Processing, 2003, Vol. 11, No. 3, pp. 255-266.
- Dong, S., Finite Difference Methods for the Hyperbolic Wave Partial Differential Equations
- Grigoryan, V., Finite differences for the wave equation
- Langtangen, H.P., Finite difference methods for wave motion
- Lie, K.-A., The Wave Equation in 1D and 2D
- Anthony Peirce, Solving the Heat, Laplace and Wave equations using finite difference methods
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions