Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part II of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Preface
This section is devoted to second order linear differential equations.
Second order systems of equations
Differential equations of arbitrary order with constant coefficients can be solved in straightforward matter by converting them into system of first order ODEs. However, they also can be solved directly, as we demonstrate shortly upon considering second order equations.
Consider a second order vector differential equation
This problem can also be solved by converting the given second order vector differential equation to the system of first order differential equations
Eigensystem[A]
Second Order Homogeneous Equations
Eigensystem[A]
Second Order Inhomogeneous Equations
Nonhomogeneous second order systems of differential equation with constant coefficients can be solved in straightforward matter based on the Laplace transform. Indeed, consider the initial value problem:
(which means that all its eigenvalues are positive)
Consider the second order vector differential equation \( \ddot{\bf x} + {\bf A}\,{\bf x} = {\bf 0} ,\) where
1& 4 & 16 \\ 18& 20 & 4 \\ -12 & -14 & -7 \end{array} \right] . \]
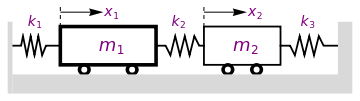
Example 11: When a system with masses connected by springs is in motion, the springs are subject to both elongation and compression. It is clear from experience that there is some force, called the restoring force, which tends to return the attached mass to its equilibrium position. According to Hooke's law, the restoring force has direction opposite to the elongation (or compression) and is proportional to the distance of the mass from its equilibrium position. The corresponding constant of proportionality is called a spring constant.
We consider a situation when two bodies of masses m1 and m2 that are connected to three springs of negligible mass having spring constants k1 k2, and k3, respectively. We denote by x1 and x2 displacement of each body from its equilibrium position.
|
mass1 = Graphics[{Thickness[0.01],
Line[{{-12.5, 0.5}, {-2.5, 0.5}, {-2.5, 4.5}, {-12.5, 4.5}, {-12.5,
0.5}}]}, Ticks -> None, Axes -> False];
mass2 = Graphics[{Thickness[0.01], Line[{{2.5, 0.5}, {2.5, 4.5}, {10.5, 4.5}, {10.5, 0.5}, {2.5, 0.5}}]}, Ticks -> None, Axes -> False]; spring1 = Graphics[{Thickness[0.005], Line[{{-12.5, 2.5}, {-14, 2.5}, {-14.4, 1.5}, {-14.8, 3.5}, {-15.2, 1.5}, {-15.6, 3.5}, {-16, 1.5}, {-16.4, 3.5}, {-16.6, 2.5}, {-17.5, 2.5}}]}, Ticks -> None, Axes -> False]; spring2 = Graphics[{Thickness[0.005], Line[{{-2.5, 2.5}, {-1.5, 2.5}, {-1, 1.5}, {-0.5, 3.5}, {0, 1.5}, {0.5, 3.5}, {1, 1.5}, {1.5, 3.5}, {2, 2.5}, {2.5, 2.5}}]}, Ticks -> None, Axes -> False]; spring3 = Graphics[{Thickness[0.005], Line[{{10.5, 2.5}, {11.5, 2.5}, {12, 1.5}, {12.5, 3.5}, {13, 1.5}, {13.5, 3.5}, {14, 1.5}, {14.5, 3.5}, {15, 2.5}, {16.5, 2.5}}]}, Ticks -> None, Axes -> False]; c1 = Graphics[{Thickness[0.01], Circle[{-10, 0}, 0.5]}]; c2 = Graphics[{Thickness[0.01], Circle[{-5, 0}, 0.5]}]; c3 = Graphics[{Thickness[0.01], Circle[{5, 0}, 0.5]}]; c4 = Graphics[{Thickness[0.01], Circle[{8, 0}, 0.5]}]; polygon = Graphics[{LightGray, Polygon[{{-17.5, -0.5}, {16.5, -0.5}, {16.5, -2.5}, {-17.5, -2.5}}]}]; poly1 = Graphics[{LightGray, Polygon[{{-17.5, -2.5}, {-18, -2.5}, {-18, 5}, {-17.5, 5}}]}];; poly2 = Graphics[{LightGray, Polygon[{{16.5, -2.5}, {18, -2.5}, {18, 5}, {16.5, 5}}]}]; l1 = Graphics[{Dashed, Line[{{-12.5, 4.5}, {-12.5, 6.5}}]}]; l2 = Graphics[{Dashed, Line[{{2.5, 4.5}, {2.5, 6.5}}]}]; a1 = Graphics[Arrow[{{-12.5, 6}, {-8, 6}}]]; a2 = Graphics[Arrow[{{2.5, 6}, {7, 6}}]]; txt1 = Graphics[ Text[Style[Subscript[x, 1], FontSize -> 14, Purple], {-7, 6}]]; txt2 = Graphics[ Text[Style[Subscript[x, 2], FontSize -> 14, Purple], {8, 6}]]; t1 = Graphics[ Text[Style[Subscript[m, 1], FontSize -> 18, Purple], {-7, 2.5}]]; t2 = Graphics[ Text[Style[Subscript[m, 2], FontSize -> 18, Purple], {7, 2.5}]]; k1 = Graphics[ Text[Style[Subscript[k, 1], FontSize -> 14, Purple], {-15, 5}]]; k2 = Graphics[ Text[Style[Subscript[k, 2], FontSize -> 14, Purple], {0, 5}]]; k3 = Graphics[ Text[Style[Subscript[k, 3], FontSize -> 14, Purple], {13.5, 5}]]; Show[mass1, mass2, spring1, spring2, spring3, c1, c2, c3, c4, polygon, poly1, poly2, l1, l2, a1, a2, txt1, txt2,t1,t2,k1,k2,k3] |
|
| Spring-mass system. | Mathematica code |
This example can be used to model several mechanical systems because there are many situations when we observe masses connected with each other. For example, a multi-story building can be considered as masses (corresponding to each floor) connecting with springs. You can model an entire set of automobiles with several hundred masses connected to each other by several undred springs and can analyze how each part of the whole car vibrates when you drive this caravan along a bumpy road. Or you can model an entire set of rail cars with several masses, one for each car and one for the locomotive, all connected to each other by several springs and then analyze how each part of the whole train vibrates when the train chugs along climbing the mountain rail. You may think this kind of simple two mass and three spring model is not adequate for complicated models from real life, but in reality the logic and process of modeling is exactly the same. You would just have several dozens of differential equations instead of two or three equations, which is very similar to what you see here.
Let x1 and x2 be displacements of masses m1 and m2, respectively, from their equilibrium positions. So we consider these variables as canonical coordinates. Then the kinetic energy of these two objects will be
Equations in not normal form
- Chi-Tsong Chen (1998). Linear System Theory and Design (3rd ed.). New York: Oxford University Press,. ISBN 978-0195117776.
- Vladimir Dobrushkin, Applied Differential Equations. The Primary Course, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043.
- Devi, J.V., Deo, S.G., Khandeparkar, R., Linear Algebra to Differential Equations, 2021, CRC Press, ISBN 9780815361466
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions