\begin{eqnarray*}
u(r, \theta ) &=& \frac{1}{\pi} \int_{-\pi}^{\pi} f(\phi )\,{\text d}\phi \left\{ \frac{1}{2} + \sum_{n\ge 1} \frac{r^n}{a^n} \,\cos n(\theta - \phi )
\right\} .
\end{eqnarray*}
We consider the sum, which is the geometric series:
\begin{eqnarray*}
\frac{1}{2} + \sum_{n\ge 1} \frac{r^n}{a^n} \,\cos n(\theta - \phi ) &=& \frac{1}{2} + \Re \,\sum_{n\ge 1} \frac{r^n}{a^n} \,e^{{\bf j} n(\theta - \phi )}
\\
&=& \frac{1}{2} + \Re \,\sum_{n\ge 1} \left( \frac{r}{a}\,e^{{\bf j} (\theta - \phi )} \right)^n
&=& \frac{1}{2} + \Re \,\dfrac{\frac{r}{a}\, e^{{\bf j} (\theta - \phi )}}{1 -\frac{r}{a}\, e^{{\bf j} (\theta - \phi )} }
\\
&=& \frac{1}{2} + \Re \,\dfrac{r\, e^{{\bf j} (\theta - \phi )}}{a - r\,e^{{\bf j} (\theta - \phi )}} ,
\end{eqnarray*}
where \( \Re \) denotes the real part of a complex number. Multiplying the numerator and denominator of the latter fraction by complex conjugate of the denominator, we obtain
\begin{eqnarray*}
\dfrac{r\, e^{{\bf j} (\theta - \phi )}}{a - r\,e^{{\bf j} (\theta - \phi )}} &=& \dfrac{r\, e^{{\bf j} (\theta - \phi )}}{a - r\,e^{{\bf j} (\theta - \phi )}} \, \frac{a - r\,e^{-{\bf j} (\theta - \phi )}}{a - r\,e^{-{\bf j} (\theta - \phi )}}
\\
&=& \frac{ra\,e^{-{\bf j} (\theta - \phi )} - r^2 }{a^2 + r^2 -2ar\,\cos (\theta - \phi )}
\end{eqnarray*}
Extracting the real part, we have
\begin{eqnarray*}
\frac{1}{2} + \sum_{n\ge 1} \frac{r^n}{a^n} \,\cos n(\theta - \phi ) &=& \frac{1}{2} + \frac{ar\,\cos (\theta - \phi ) - r^2}{a^2 + r^2 -2ar\,\cos (\theta - \phi )}
\\
&=& \frac{1}{2}\,\frac{a^2 - r^2}{a^2 + r^2 -2ar\,\cos (\theta - \phi )} .
\end{eqnarray*}
This results in Poisson’s formula
\begin{equation} \label{EqPolar.4}
u(r, \theta ) = \frac{1}{2\pi} \,\int_0^{2\pi} f(\phi ) \,P_r (\theta - \phi )\,{\text d}\phi , \qquad P_r (x) = \frac{a^2 - r^2}{a^2 + r^2 -2ar\,\cos x} , \quad r \le a.
\end{equation}
At r = 0, the integral is easy to compute:
\[
u(0, \theta ) = \frac{1}{2\pi} \,\int_0^{2\pi} f(\phi ) \,{\text d}\phi = \frac{1}{2\pi} \,\int_0^{2\pi} u(a, \phi ) \,{\text d}\phi .
\]
Therefore, we can make the following conclusions.
If u is a solution of the Laplace equation Δu = 0, then the value of u at any point is just the average values of
u on a circle centered on that point. ("Mean value theorem")
The maximum and minimum values of u are therefore
always on the domain boundary (this is true for any smooth shape
domain).
Example 1: Dirichlet problem with piecewise continuous input
Example 1: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 0 \le r < 2, \qquad u(2, \theta ) = f(\theta ) \equiv \begin{cases} 1, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi . \end{cases} .
\]
Its solution is known to be
\[
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{r}{2} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le r \le 2, \quad 0\le \theta \le 2\pi .
\]
To satisfy the boundary condition
\( u(2, \theta ) = f(\theta ) , \) we calculate the coefficients as usual
\begin{eqnarray*}
a_0 &=& \frac{1}{\pi} \int_0^{\pi} {\text d}\phi + \frac{1}{\pi} \int_0^{\pi} \cos^2 \phi \,{\text d}\phi = \frac{3}{2} ,
\\
a_n &=& \frac{1}{\pi} \int_0^{\pi} \cos (n\phi ) \, {\text d}\phi + \frac{1}{\pi} \int_0^{\pi} \cos (n\phi ) \, \cos^2 \phi \,{\text d}\phi = \begin{cases} \frac{1}{4} , & \ \mbox{ if } n=2, \\
0, & \ \mbox{ if } n \ne 2; \end{cases}
\\
b_n &=& \frac{1}{\pi} \int_0^{\pi} \sin (n\phi ) \, {\text d}\phi + \frac{1}{\pi} \int_0^{\pi} \sin (n\phi ) \, \cos^2 \phi \,{\text d}\phi = \begin{cases} \frac{-4}{n\left( n^2 -4 \right)} , & \ \mbox{ if $n$ is odd}, \\
0, & \ \mbox{ if } n \mbox{ is even}; \end{cases}
\end{eqnarray*}
because Mathematica helps
a0 := (1/Pi)*(Integrate[1, {x, 0, Pi}] +
Integrate[(Cos[x])^2 , {x, Pi, 2*Pi}])
Therefore, the required solution is
\[
u(r, \theta ) = \frac{3}{4} + \frac{r^2}{16}\,\cos 2\theta - \frac{4}{\pi}\,\sum_{k\ge 0} \frac{1}{(2k+1) \left[ (2k+1)^2 -4 \right]} \left( \frac{r}{2} \right)^{2k+1} \sin (2k+1)\theta .
\]
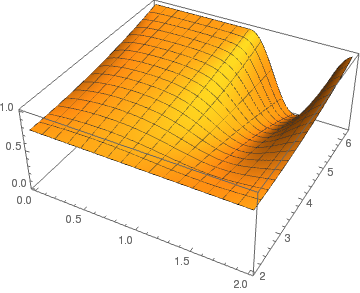
Now we plot the solution using Mathematica . The first step in constructing our table is to define the function and build a table of height values according to the found solution.
u[r_, t_] := )
Now we can plot the table of data in Cartesian coordinates by using ListPlot3D :
graph = ListPlot3D[data, DataRange -> {{0, 2}, {2, 2*Pi}}]
Solution in rectangular coordinates
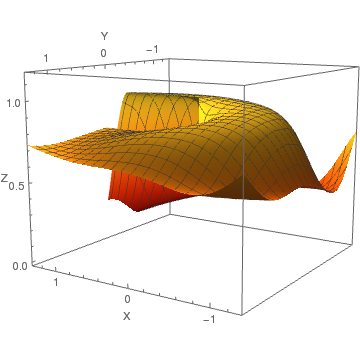
Next we convert the graph into polar coordinates. First, we define the subroutine:
MyListPolarPlot3D[data_, rRange_, thetaRange_, zRange_] :=
Finally, we plot our data in polar coordinates:
MyListPolarPlot3D[data, {0.0, 2.0}, {0.0, 2*Pi}, {0, 1.15}]
Solution in polar coordinates
Example 2: Dirichlet problem with harmonic input
Example 2: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 0 \le r < 3, \qquad u(3, \theta ) =
2\sin 4\theta - 3\,\cos 7\theta .
\]
Its solution is known to be
\[
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{r}{3} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le r \le 3, \quad 0\le \theta \le 2\pi .
\]
To satisfy the boundary condition
\( u(2, \theta ) = f(\theta ) , \) we don't need to use Euler's formalae because we have expansion
\[
u(3, \theta ) = f(\theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le r \le 3, \quad 0\le \theta \le 2\pi ,
\]
where f is a combination of eigenfunctions. So we know that all coefficients in the above expansion are zeroes except n = 4 and n = 7. Hence,
\[
b_4 =2 \qquad\mbox{and} \qquad a_7 = -3 .
\]
This yields
\[
u(r, \theta ) = 2 \left( \frac{r}{3} \right)^4 \sin 4\theta -3 \left( \frac{r}{3} \right)^7 \sin 7\theta .
\]
Dirichlet Problem outside the circle
Consider the exterior Dirichlet problem for a circle of radius a :
\[
u_{rr} + \frac{1}{r}\,u_r + \frac{1}{r^2}\,u_{\theta\theta} =0, \qquad r> a, \qquad u(a,\theta ) = f(\theta ) ,
\]
where f is a given function. Its general solution can be expressed as
\begin{equation} \label{EqPolar.5}
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{a}{r} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r>a, \quad 0\le \theta \le 2\pi .
\end{equation}
The coefficients of the above sum are obtained from the boundary conditions that lead to Poisson’s formula
\[
u(r, \theta ) = \frac{1}{2\pi} \,\int_0^{2\pi} f(\phi ) \,P_r (\theta - \phi )\,{\text d}\phi , \qquad P_r (x) = \frac{r^2 - a^2}{a^2 + r^2 -2ar\,\cos x} , \quad a \le r.
\]
Example 3: Dirichlet exterior problem with piecewise continuous input
Example 3: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 2 \le r , \qquad u(2, \theta ) = f(\theta ) \equiv \begin{cases} 1, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi . \end{cases} .
\]
Its solution is known to be
\[
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{2}{r} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 2\le r , \quad 0\le \theta \le 2\pi .
\]
The above series satisfies the boundary condition only when
\[
u(2, \theta ) = f(\theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le \theta \le 2\pi .
\]
The explicit values of these coefficients were found previously, and we get the required solution:
\[
u(r, \theta ) = \frac{3}{4} + \frac{1}{r^2}\,\cos 2\theta - \frac{4}{\pi}\,\sum_{k\ge 0} \frac{1}{(2k+1) \left[ (2k+1)^2 -4 \right]} \left( \frac{2}{r} \right)^{2k+1} \sin (2k+1)\theta .
\]
Example 4: Dirichlet exterior problem with harmonic input
Example 4: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 3 < r, \qquad u(3, \theta ) =
2\sin 4\theta - 3\,\cos 7\theta .
\]
A solution of Laplace's equation in outside the circle is known to be
\[
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{3}{r} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r>3, \quad 0\le \theta \le 2\pi .
\]
Since the input function is a linear combination of eigenfunctions, we conclude that all coefficients in the above series are zeroes except
n = 4 and
n = 7:
\[
u(r, \theta ) = 2 \left( \frac{3}{r} \right)^4 \sin 4\theta - 3 \left( \frac{3}{r} \right)^7 \sin 7\theta .
\]
Neumann Problem inside the circle
Consider the interior Neumann problem for a circle of radius a :
\[
u_{rr} + \frac{1}{r}\,u_r + \frac{1}{r^2}\,u_{\theta\theta} =0, \qquad 0 \le r< a, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=a} = g(\theta ) , \qquad \int_0^{2\pi} g(\theta )\,{\text d}\theta = 0 ,
\]
where g is a given function. The general solution of Laplace's equation inside a circle of radius a is
\begin{equation} \label{EqPolar.6}
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{r}{a} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0 \le r<a, \quad 0\le \theta \le 2\pi .
\end{equation}
Its derivative with respect to r becomes (assuming uniform convergence of the above series)
\[
\frac{\partial u}{\partial r} = \sum_{n\ge 1} \frac{n}{r} \left( \frac{r}{a} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0 \le r<a, \quad 0\le \theta \le 2\pi .
\]
Setting r equals to a yields
\[
\left. \frac{\partial u}{\partial r} \right\vert_{r=a} = g(\theta ) = \sum_{n\ge 1} \frac{n}{a}
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le \theta \le 2\pi .
\]
The coefficients of the Fourier series are calculated according to Euler's formulae
\begin{eqnarray*}
a_0 &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\,{\text d}\phi =0 ,
\\
\frac{n}{a}\,a_n &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\,\cos (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots ;
\\
\frac{n}{a}\,b_n &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\, \sin (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots .
\end{eqnarray*}
Note that the coefficient a 0 must be zero because the corresponding Fourier series for
\[
\left. \frac{\partial u}{\partial r} \right\vert_{r=a} = \sum_{n\ge 1} \frac{n}{a}
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le \theta \le 2\pi ;
\]
does not contain a free term. Therefore, a Neumann problem has a solution if and only if the integral over the boundary vanishes:
\[
\int_0^{2\pi} g(\phi )\,{\text d}\phi =0 .
\]
Then the general solution to a Neumann problem is not unique but up to an arbitrary additive constant:
\begin{eqnarray*}
u(r, \theta ) &=& C + \sum_{n\ge 1} \left( \frac{r}{a} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right]
\\
&=& C + \sum_{n\ge 1} \left( \frac{r}{a} \right)^n
\left[ \frac{a}{n\pi} \,\int_0^{2\pi} g(\phi )\,\cos n\phi \,{\text d}\phi \, \cos n\theta + \frac{a}{n\pi} \,\int_0^{2\pi} g(\phi )\,\sin n\phi \,{\text d}\phi \, \sin n\theta \right]
\\
&=& C + \frac{a}{\pi} \,\sum_{n\ge 1} \left( \frac{r}{a} \right)^n \int_0^{2\pi} {\text d}\phi \, \cos n \left( \theta - \phi \right) \frac{1}{n}
\\
&=& C + \frac{a}{\pi} \,\Re\,\sum_{n\ge 1} \frac{1}{n} \left( \frac{r}{a}\, e^{{\bf j} (\theta - \phi )} \right)^n
\\
&=& C - \frac{a}{\pi} \,\Re\,\ln \left( 1 - \frac{r}{a}\, e^{{\bf j} (\theta - \phi )} \right)
\end{eqnarray*}
since according to Mathematica
Sum[z^n /n, {n, 1, Infinity} ]
-Log[1 - z]
We are not going to simplify the above formula because it requires a solid knowledge of functions of a complex variable.
Example 5: Neumann interior problem with piecewise continuous input
Example 5: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 0 \le r < 5, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=5} = g(\theta ) \equiv \begin{cases} -1/2, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi . \end{cases} .
\]
The general solution of the Neumann problem for Laplace's equation is known to be
\[
u(r, \theta ) = C + \sum_{n\ge 1} \left( \frac{r}{5} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad 0\le r \le 5, \quad 0\le \theta \le 2\pi ;
\]
where
C is an arbitrary constant. The given problem has a solution only if the integral of
g over the boundary is zero.
Mathematica helps
Integrate[(Cos[x])^2, {x, Pi, 2*Pi}]/Pi -
Integrate[1/2, {x, 0, Pi}]/Pi
0
Next we calculate coefficients in the Fourier series
\begin{eqnarray*}
a_n &=& \frac{5}{n\pi} \int_0^{2\pi} g(\phi )\,\cos (n\phi ) \, {\text d}\phi = \begin{cases} 0, & \ \mbox{ for } n \ne 2, \\ \frac{5}{8} , & \ \mbox{ for } n=2; \end{cases} \qquad n=1,2,\ldots ;
\\
b_n &=& \frac{5}{n\pi} \int_0^{2\pi} g(\phi )\, \sin (n\phi ) \, {\text d}\phi = \begin{cases} 0, & \ \mbox{ for &n& even}, \\ -\frac{5 \left( 3n^2 -8 \right)}{n^2 \left( n^2 -4 \right) \pi} , & \ \mbox{ for $n$ odd}; \end{cases} \qquad n=1,2,\ldots .
\end{eqnarray*}
a[n_] := 5*Integrate[Cos[n*x]*(Cos[x])^2, {x, Pi, 2*Pi}]/Pi /n -
5*Integrate[1/2*Cos[n*x], {x, 0, Pi}]/Pi/n
Therefore, the solution becomes
\[
u(r, \theta ) = C + \frac{r^2}{40}\,\cos 2\theta - \sum_{k\ge 0} \frac{3(2k+1)^2 -8}{(2k+1)^2 \left( (2k+1)^2 -4 \right)} \left( \frac{r}{5} \right)^{2k+1} \sin (2k+1)\theta , \qquad 0\le r \le 5, \quad 0\le \theta \le 2\pi .
\]
Example 6: Neumann interior problem with harmonic input
Example 6: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 0 \le r < 5, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=5} = f(\theta ) \equiv
2\sin 4\theta - 3\,\cos 7\theta .
\]
First, we check with
Mathematica that the given Neumann problem has a solution:
Integrate[2*Sin[4*x] - 3*Cos[7*x], {x,0,2*Pi}]
0
Then we substitute the general solution
\[
u(r, \theta ) = C + \sum_{n\ge 1} \left( \frac{r}{5} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right]
\]
into the boundary condition
\[
\left. \frac{\partial u}{\partial r} \right\vert_{r=5} = \sum_{n\ge 1} \left. \left. \frac{n}{5} \left( \frac{r}{5} \right)^n \right\vert_{r=5}
\left[ a_n \cos n\theta + b_n \sin n\theta \right] = 2\sin 4\theta - 3\,\cos 7\theta .
\]
Comparison of both sides leads to conclusion that all coefficients of the Fourier series are zeroes except two indices:
\[
\frac{7}{5} \, a_7 = -3, \qquad\mbox{and} \qquad \frac{4}{5} \, b_4 = 2 .
\]
Hence, the required solution becomes
\[
u(r, \theta ) = C + \frac{5}{2} \left( \frac{r}{5} \right)^4 \sin 4\theta - \frac{15}{7} \left( \frac{r}{5} \right)^7 \sin 7\theta .
\]
Neumann Problem outside the circle
Consider the exterior Neumann problem for a circle of radius 𝑎:
\[
u_{rr} + \frac{1}{r}\,u_r + \frac{1}{r^2}\,u_{\theta\theta} =0, \qquad r> a, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=a} = g(\theta ) , \qquad \int_0^{2\pi} g(\theta )\,{\text d}\theta = 0 ,
\]
where g is a given function. Note that the Neumann problem has no solution if the integral of the given function g over the circumference (which is the boundary of the circle) is not zero. The general solution of Laplace's equation outside a circle of radius 𝑎 is
\[
u(r, \theta ) = \frac{a_0}{2} + \sum_{n\ge 1} \left( \frac{a}{r} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r>a, \quad 0\le \theta \le 2\pi .
\]
Its derivative with respect to r becomes (assuming uniform convergence of the above series)
\[
\frac{\partial u}{\partial r} = - \sum_{n\ge 1} \frac{n}{r} \left( \frac{a}{r} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r>a, \quad 0\le \theta \le 2\pi .
\]
To satisfy the boundary condition, we have to check validity of
\[
\lim_{r\to a} \,\frac{\partial u}{\partial r} = - \sum_{n\ge 1} \frac{n}{a}
\left[ a_n \cos n\theta + b_n \sin n\theta \right] = g(\theta ), \qquad 0\le \theta \le 2\pi .
\]
Since the last identity is just the Fourier series for the given function g , we find the coefficients according to Euler's formulae:
\begin{eqnarray*}
a_0 &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\,{\text d}\phi =0 ,
\\
-\frac{n}{a}\,a_n &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\,\cos (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots ;
\\
-\frac{n}{a}\,b_n &=& \frac{1}{\pi} \int_0^{2\pi} g(\phi )\, \sin (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots .
\end{eqnarray*}
This allows us to determine the solution of exterior Neumann problem outside the circle:
\[
u(r, \theta ) = C + \sum_{n\ge 1} \left( \frac{a}{r} \right)^n
\left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r>a, \quad 0\le \theta \le 2\pi ,
\]
where C is an arbitrary constant and
\begin{eqnarray*}
a_n &=& -\frac{a}{n\pi} \int_0^{2\pi} g(\phi )\,\cos (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots ;
\\
b_n &=& -\frac{a}{n\pi} \int_0^{2\pi} g(\phi )\, \sin (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots .
\end{eqnarray*}
Example 7: Neumann exterior problem with piecewise continuous input
Example 7: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 5 < r, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=5} = f(\theta ) \equiv \begin{cases} -1/2, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi . \end{cases} .
\]
Its solution is known to be
\[
u(r, \theta ) = C + \sum_{n\ge 1} \left( \frac{5}{r} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r \ge 5, \quad 0\le \theta \le 2\pi ,
\]
where
C is an arbitrary constant. We determine the values of coefficients from known formulas:
\begin{eqnarray*}
a_n &=& -\frac{5}{n\pi} \int_0^{2\pi} g(\phi )\,\cos (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots ;
\\
b_n &=& -\frac{5}{n\pi} \int_0^{2\pi} g(\phi )\, \sin (n\phi ) \, {\text d}\phi , \qquad n=1,2,\ldots ;
\end{eqnarray*}
that were evaluated in the previous example. Thus, we get
\[
u(r, \theta ) = C - \frac{r^2}{40}\,\cos 2\theta + \sum_{k\ge 0} \frac{3(2k+1)^2 -8}{(2k+1)^2 \left( (2k+1)^2 -4 \right)} \left( \frac{5}{r} \right)^{2k+1} \sin (2k+1)\theta , \qquad r \ge 5, \quad 0\le \theta \le 2\pi .
\]
Example 8: Neumann exterior problem with harmonic input
Example 8: :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad r > 4, \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=4} = g(\theta ) \equiv
2\sin 4\theta - 3\,\cos 7\theta .
\]
Substituting the general solution (which is assumed to be represented through a uniformly convergent series)
\[
u(r, \theta ) = C + \sum_{n\ge 1} \left( \frac{4}{r} \right)^n \left[ a_n \cos n\theta + b_n \sin n\theta \right] , \qquad r \ge 4, \quad 0\le \theta \le 2\pi ,
\]
where
C is an arbitrary constant, into the boundary condition
\[
\lim_{r\to 4} \, \frac{\partial u}{\partial r} = - \sum_{n\ge 1} \frac{n}{4} \left[ a_n \cos n\theta + b_n \sin n\theta \right] =
2\sin 4\theta - 3\,\cos 7\theta ,
\]
we see that all coefficients must be zeroes, but two of them not:
\[
b_4 = -2 \qquad\mbox{and} \qquad a_7 = \frac{12}{7} .
\]
So
\[
u(r, \theta ) = C + \frac{12}{7} \left( \frac{4}{r} \right)^7 \cos 7\theta - 2 \left( \frac{4}{r} \right)^4 \sin 4\theta , \qquad r \ge 4, \quad 0\le \theta \le 2\pi .
\]
Laplace Equation in a Donut
We consider boundary value problems inside the domain bounded by two circles, which is usually called a donut.
In Mathematica , we plot a donut as follows.
RegionPlot[1 < Abs[x + I y] < 2, {x, -2, 2}, {y, -2, 2}, ImagePadding -> 1, PlotStyle -> Blue]
Example: Mixed boundary value problem for donut domain
Example :
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} = 0 , \qquad 2 \le r < 5, \qquad u(2, \theta ) = f(\theta ) \equiv \begin{cases} 1, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi ; \end{cases} \qquad \left. \frac{\partial u}{\partial r} \right\vert_{r=5} = g(\theta ) \equiv
2\sin 4\theta - 3\,\cos 7\theta .
\]
The general solution to Laplace's equation is known to be
\[
u(r, \theta ) = \frac{a_0}{2} + d_0\ln r + \sum_{n\ge 1} \left( \frac{r}{2} \right)^n \left[ a_n \cos \left( n \theta \right) + b_n \sin \left( n \theta \right) \right] + \sum_{n\ge 1} \left( \frac{5}{r} \right)^n \left[ c_n \cos \left( n \theta \right) + d_n \sin \left( n \theta \right) \right] .
\]
This function will be a required solution if the following boundary conditions hold:
\begin{eqnarray*}
u(2, \theta ) &=& \frac{a_0}{2} + d_0\ln 2 + \sum_{n\ge 1} \left[ a_n \cos \left( n \theta \right) + b_n \sin \left( n \theta \right) \right] + \sum_{n\ge 1} \left( \frac{5}{2} \right)^n \left[ c_n \cos \left( n \theta \right) + d_n \sin \left( n \theta \right) \right]
\\
&=& \frac{a_0}{2} + d_0\ln 2 + \sum_{n\ge 1} \left[ a_n + \left( \frac{5}{2} \right)^n c_n \right] \cos \left( n \theta \right) + \sum_{n\ge 1} \left[ b_n + \left( \frac{5}{2} \right)^n d_n \right] \sin \left( n \theta \right) = f(\theta ) \equiv \begin{cases} 1, & \ \mbox{if } 0 \le \theta \le \pi , \\ \cos^2 \theta , & \ \mbox{if } \pi \le \theta \le 2\pi ; \end{cases}
\\
\left. \frac{\partial u}{\partial r} \right\vert_{r=5} &=& \frac{d_0}{5} + \sum_{n\ge 1} \left[ \frac{n}{5} \left( \frac{5}{2} \right)^n a_n - \frac{n}{5}\, c_n \right] \cos \left( n \theta \right) + \sum_{n\ge 1} \left[ \frac{n}{5} \left( \frac{5}{2} \right)^n b_n - \frac{n}{5}\, d_n \right] \sin \left( n \theta \right) = 2\sin 4\theta - 3\,\cos 7\theta .
\end{eqnarray*}
Since the function
f has the Fourier expansion
\[
f(\theta ) = \frac{3}{4} + \frac{1}{4}\,\cos 2\theta - \sum_{k\ge 0} \frac{4}{(2k+1) \left( (2k+1)^2 -4 \right)} \,\sin (2k+1)\theta ,
\]
and the function
g is itself the Fourier series, we get the following system of algebraic equations:
\begin{eqnarray*}
\frac{3}{4} &=& \frac{a_0}{2} + d_0\ln 2 ,
\\
\frac{1}{4}\,\delta_{2,n} &=& a_n + \left( \frac{5}{2} \right)^n c_n ,
\\
- \frac{4}{(2k+1) \left( (2k+1)^2 -4 \right)} &=& b_{2k+1} + \left( \frac{5}{2} \right)^{2k+1} c_{2k+1} ,
\\
0 &=& b_{2k} + \left( \frac{5}{2} \right)^{2k} c_{2k} ,
\\
\frac{d_0}{5} &=& 0 ,
\\
\frac{n}{5} \left( \frac{5}{2} \right)^n a_n - \frac{n}{5}\, c_n &=& -3\,\delta_{n,4}
\\
\frac{n}{5} \left( \frac{5}{2} \right)^n b_n - \frac{n}{5}\, d_n &=& 2\,\delta_{7,n} ,
\end{eqnarray*}
where δ is the
delta-symbol of
Kronecker :
\[
\delta_{i,j} = \begin{cases} 0, & \ \mbox{if } i \ne j, \\
1, & \ \mbox{if } i=j .
\end{cases}
\]
The initial coefficients are
\( c_0 = \frac{3}{2} , \quad d_0 =0 . \) Some other coefficients could be related by
\[
a_n = - c_n \left( \frac{5}{2} \right)^{2k} c_{2k} , \quad n \ne 2, \qquad b_{2k} = - \left( \frac{5}{2} \right)^{2k} c_{2k} , \qquad c_n = a_n \left( \frac{5}{2} \right)^{n} \quad n \ne 4, \qquad d_n = b_n \left( \frac{5}{2} \right)^{n} \quad n \ne 7.
\]
For other coefficients, we ask
Mathematica for help:
Example: Dirichlet problem inside annulus without a solution
Example :
\[
u_{xx} + u_{yy} = 0 \quad (0 < x^2 + y^2 < 1), \qquad \left. u \right\vert_{\partial\Omega} = f = \begin{cases}
0, & \ \mbox{ on }\quad x^2 + y^2 = 1, \\
1, & \ \mbox{ at }\quad (0,0) .
\end{cases}
\]
In this case, the condition that
f on the boundary ((
x ² +
y ² = 1) ∪ (0,0)) is continuous is relaxed somewhat (17. page 138--139)
By symmetry and uniqueness, it is obvious that is the given problem has a solution, it must have a rotational symmetry (that is, the solution must be a function of \( \displaystyle r = \sqrt{x^2 + y^2} , \) independent of the polar angle θ). )
It is clear that the solution of the given problem must be of the form
\[
u = u(r) = a\,\ln r + b,
\]
where costants 𝑎 and
b are to be determiined from the bpundary conditions:
\[
u (r=1) = b = 0 .
\]
If 𝑎 ≠ 0, then
u is unbounded near the origin. In any way, the second boundary condition at the origin cannot be satisfied.
■
Dirichlet Problem inside a cylinder
In cylindrical coordinates, Laplace's equation is written
\[
\frac{1}{r} \, \frac{\partial}{\partial r} \left( r\,\frac{\partial u}{\partial r} \right) + \frac{1}{r^2 } \, \frac{\partial^2 u}{\partial \theta^2} + \frac{\partial^2 u}{\partial z^2} = 0 , \qquad 0 \le r < a, \quad 0 < z < \ell .
\]
We will specify Dirichlet boundary conditions later. We we concentrate on finding the general solution using separation of variables:
\[
u(r, \theta , z ) = R(r)\, \Theta (\theta )\,Z(z) .
\]
Substitution of the above form into the Laplace equation yields
\[
\begin{split}
\frac{{\text d}^2 Z}{{\text d} z^2} - k^2 Z &= 0 ,
\\
\frac{{\text d}^2 \Theta}{{\text d}\theta^2} + \lambda^2 \Theta &= 0 ,
\\
\frac{{\text d}^2 R}{{\text d} r^2} + \frac{1}{r}\,\frac{{\text d}R}{{\text d}r} + \left( k^2 - \frac{\lambda^2}{r^2} \right) R(r) &=0 .
\end{split}
\]
For Θ we get the Sturm--Liouville problem
\[
\Theta'' + \lambda^2 \Theta (\theta ) =0, \qquad \Theta (\theta ) = \Theta (\theta + 2\pi ) .
\]
Return to Mathematica page
Return to the main page (APMA0340) Part 1 Matrix Algebra Part 2 Linear Systems of Ordinary Differential Equations Part 3 Non-linear Systems of Ordinary Differential Equations Part 4 Numerical Methods Part 5 Fourier Series Part 6 Partial Differential EquationsPart 7 Special Functions