Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to the main page for the fourth course APMA0360
Return to Part VII of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Preface
The Mathieu equation is an ordinary differential equation with real coefficients. Its standard form with parameters (a, q) is
On the complex plane, an equivalent relationship is
{\[Alpha] = 1},
Framed[
ParametricPlot[
{
\[Alpha]*Cosh[\[Mu]]*Cos[\[Theta]],
\[Alpha]*Sinh[\[Mu]]*Sin[\[Theta]]
},
{\[Mu], -2, 2},
{\[Theta], 0, Pi},
PlotRange -> 2*{{-1, 1}, {-1, 1}},
Mesh -> True,
PlotStyle -> None,
MeshFunctions -> {#3 &, #4 &},
MeshStyle -> {
Directive[Opacity[1], Thickness[0.003], Green],
Directive[Opacity[1], Thickness[0.003], Blue]
},
Epilog -> {Red, PointSize -> 0.02,
Point[{{-\[Alpha], 0}, {\[Alpha], 0}}]},
Frame -> False,
Ticks -> {None, Range[0, 10, 0.2]},
GridLines -> Automatic ],
FrameStyle -> Gray, FrameMargins -> 0 ]
]
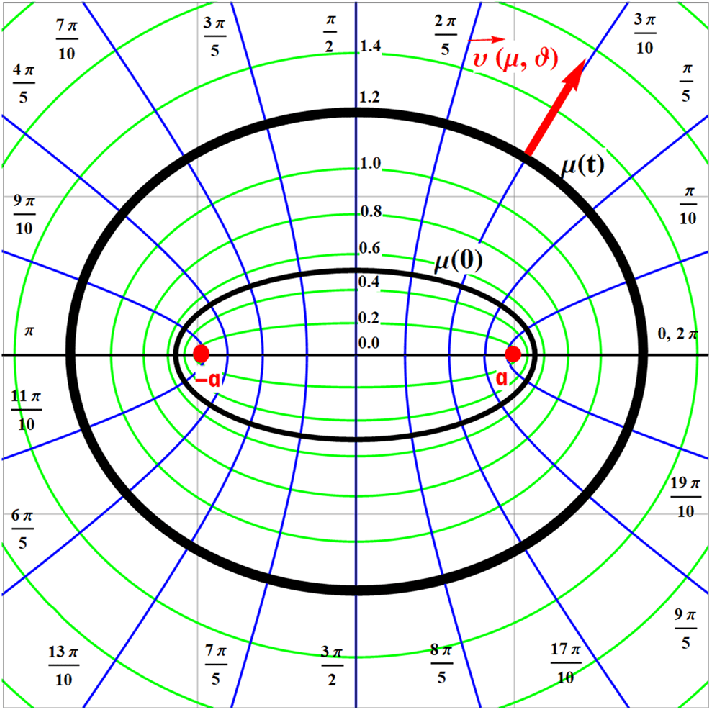

To create an ellipse, fix the value of ξ:
Use Show to combine two parametric plots:
Calculate the radius of an ellipse
The radius of each ellipse is given by the following code:
This expression simplifies at the points where the ellipse crosses the axes (that is, when η = 0, η = π/2, η = π or η = (3π)/2):
| Eta | Radius | |
| 0 | Abs[\[Alpha] Cosh[\[Mu]]] | |
| π/2 | Abs[\[Alpha] Sinh[\[Mu]]] | |
| π | Abs[\[Alpha] Cosh[\[Mu]] | |
| 3π/2 | Abs[\[Alpha] Sinh[\[Mu]] |
Experiment with ξ and η
Change the value of ξ:
Change the value of θ:
Mathieu Functions
However, Mathieu's equation and its generalisations are more important than this single application would suggest. This equation is encountered in many different issues in physics, engineering and industry, including the stability of floating ships and railroad trains, the motion of charged particles in electromagnetic Paul traps, the theory of resonant inertial sensors, and many other problem (see expositions by McLachlan and Ruby).
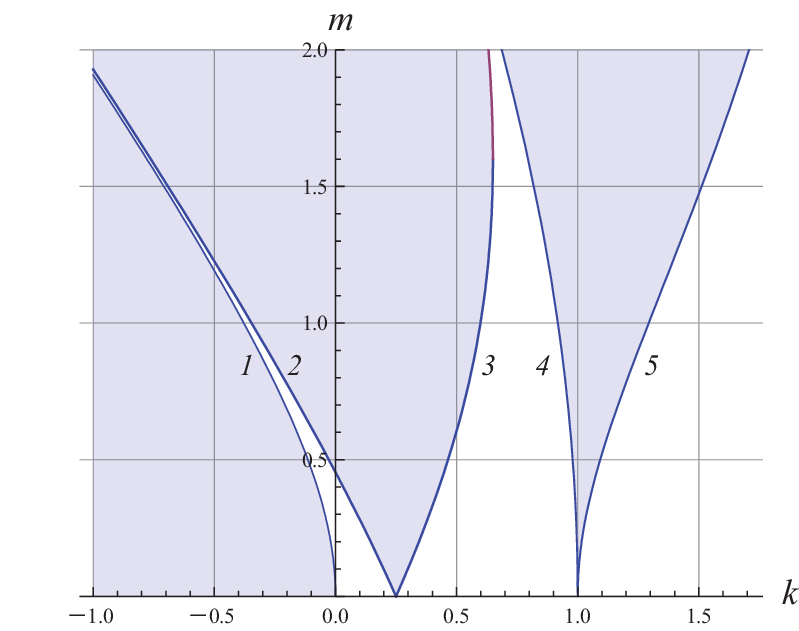
The Mathieu equation has two types of solutions---stable and unstable, depending only on parameters 𝑎 and q and not on the initial conditions.
|
Mathieu Stability Chart plots the stable and unstable zones in the plane is known as the Ince--Strutt diagram.
y1[x_] = 2*Sqrt[(x*(x - 1)*(x - 4))/(3*x - 8)];
p1 = Plot[y1[x], {x, -1, 0}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, Filling -> Axis, PlotRange -> {-1, 2}]; y2[x_] = .25*((((9 - 4*x)*(13 - 20*x))^{1/2}) - (9 - 4*x)); p2 = Plot[y2[x], {x, -1, 1/4}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, Filling -> Top, PlotRange -> {-1, 2}]; y3[x_] = (1/4)*((9 - 4*x) - ((9 - 4*x)*(13 - 20*x))^(.5)); p3 = Plot[y3[x], {x, 1/4, 13/20}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, Filling -> Top, PlotRange -> {-1, 2}]; y4[x_] = .25*((9 - 4*x) + ((9 - 4*x)*(13 - 20*x))^(.5)); p4 = Plot[y4[x], {x, 1/4, 13/20}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, Filling -> Top, PlotRange -> {-1, 2}]; y5[x_] = ((2*(x - 1)*(x - 4)*(x - 9))/(x - 5))^(.5); p5 = Plot[y5[x], {x, 13/20, 1}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, Filling -> Top, PlotRange -> {-1, 2}]; y6[x_] = 2*((x*(x - 1)*(x - 4))/(3*x - 8))^(.5); p6 = Plot[y6[x], {x, 1, 2}, PlotStyle -> Thickness[0.01], AspectRatio -> 1, PlotRange -> {-1, 2}, Filling -> Top]; Show[p1, p2, p3, p4, p5, p6, PlotRange -> {-1, 2}] |
|
| Fig.1 Ince-Strutt diagram. | Mathematica code. |
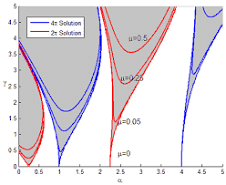
It is convenient to write Mathieu equation using a slightly different notation from that in Eq. \eqref{EqMathieu.1}, a notation which will be more convenient for our further discussion, namely, as
E.Butikov showed that the transition curves of the Ince-Strutt diagram can be determined by equations:
Let us consider the one-dimensional version of this problem. The wavefunction of the electron then satisfies the one-dimensional Schrodinger equation in which the potential V(x) is a periodic function. Suppose that the period is a, so that V(x+a)=V(x). Then, after making the change of variables
the normalized wavefunction u(x) and energy parameter λ satisfy
where \( q(x+1) =q(x) . \)
We consider this Sturm--Liouville problem on the
real line with a general 1-periodic potential q(x), assumed continuous.
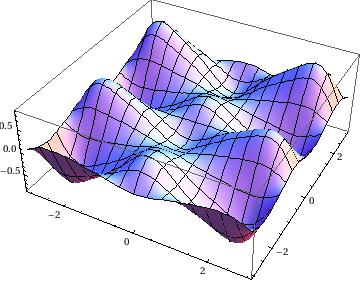
A specific example of such an equation is the Mathieu equation:
where k is a real paarmeter. Its solutions, called the Mathieu functions, have been studied extensively.
Next we plot Mathieu function:
- Allievi, A. and Soudack, A., Ship stability via the Mathieu equation, International Journal of Control, 1990, Volume 51, Issue 1, pp. 139--167. https://doi.org/10.1080/00207179008934054
- Butikov, Eugene I., Analytical expressions for stability regions in the Ince–Strutt diagram of Mathieu eqution, American Journal of Physics, 86, Isuue 4, 257 (2018); https://doi.org/10.1119/1.5021895
- Daniel, D.J., Exact solutions of Mathieu’s equation, Progress of Theoretical and Experimental Physics, 2020, Volume 2020, Issue 4, April 2020, 043A01, https://doi.org/10.1093/ptep/ptaa024
- Jovanoski, Z. and Robinson, G., Ship Stability and Parametric Rolling, Australasian Journal of Engineering Education, Volume 15, 2009 - Issue 2, pp. 43--50. https://doi.org/10.1080/22054952.2009.11464028
- Mathieu, É.L., Memoir on vibrations of an elliptic membrane, 1868; Mémoire sur le mouvement vibratoire d'une membrane de forme elliptique, Journal de Mathématiques Pures et Appliquées 13, 137–203 (1868);
- McLachlan, N.W., Theory of Application of Mathieu Functions, Dover, New York, 1964.
- Paul, W., Electromagnetic traps for charged and neutral particles, Reviews of Modern Physics, 1990, Vol. 62, No. 3, pp. 531--540. http://dx.doi.org/10.1103/RevModPhys.62.531 )
- Rand, R.H., Lecture Notes in Nonlinear Vibrations (new edition). Published on-line by The Internet-First University Press (Cornell's digital repository), 2012.
- Ruby, L., Applications of the Mathieu equation, American Journal of Physics, 1995, Volume 64, Issue 1 https://doi.org/10.1119/1.18290
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions