Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course Return to Mathematica tutorial for the fourth course APMA0340
APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part V of the course APMA0330

Glossary

Preface

Figures with Arrows

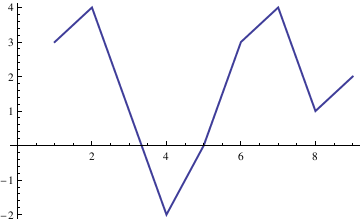
When one wants to plot a figure that is built from straight lines, it can be done as follows

     
ListLinePlot[{3, 4, 1, -2, 0, 3, 4, 1, 2}, PlotStyle->Thick]
       LinePlot in action.            Mathematica code

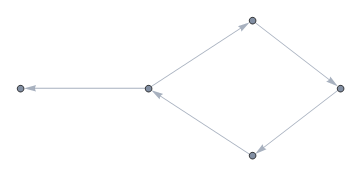
A directed graph can be plotted as well

     
Graph[{1 -> 3, 1 -> 2, 2 -> 4, 4 -> 5, 5 -> 1}]
       Directed graph.            Mathematica code

     
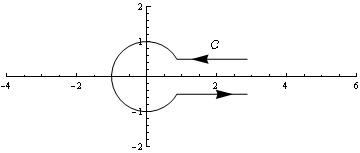
With[{q = Pi/6},
Graphics[{Circle[{0, 0}, 1, {q, 2 Pi - q}],
Arrowheads[{{.05, .8}}],
Arrow[{{Cos[q] + 2, Sin[q]}, {Cos[q], Sin[q]}}],
Arrow[{{Cos[q], Sin[-q]}, {Cos[q] + 2, Sin[-q]}}],
FontSize -> Medium, Text["\[ScriptCapitalC]", {2, Sin[q]}, {0, -2}]},
Axes -> True, PlotRange -> {{-4, 6}, {-2, 2}}]]
       Traverse a cut.            Mathematica code

 

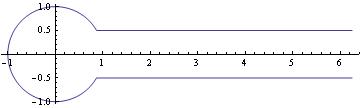
If you want to plot the actual contour without arrows, then try something like the following:

     
contour[t_, t0_: (5 Pi/6)] := Piecewise[{ {Exp[I (t + Pi)], -t0 < t < t0},
{t - t0 + Exp[I (t0 + Pi)], t >= t0}, {-t - t0 + Exp[-I (t0 + Pi)], t <= -t0}}]
ParametricPlot[Through[{Re, Im}[contour[t]]], {t, -8, 8}, PlotPoints -> 30]
       Traverse a cut.            Mathematica code

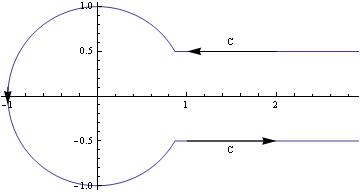
Another option:

     
c = 0.5;
t0 = ArcSin[c];
PolarPlot[If[Abs[t] < t0, Abs[Sin[t0]/Sin[t]], 1], {t, -\[Pi], \[Pi]},
Epilog -> { Arrow[{{2, c}, {1, c}}], Arrow[{{1, -c}, {2, -c}}], Arrow[{{-1, .1}, {-1, -.1}}],
Text["C", {1.5, c + .1}], Text["C", {1.5, -(c + .1)}] }]
       Traverse a cut.            Mathematica code

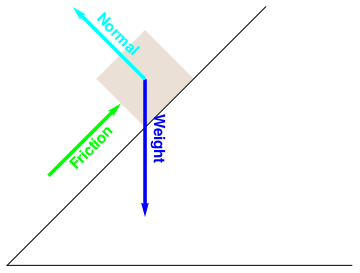
Now we show how to add arrows into the graph.

g1=Graphics[Line[{{0,0},{20,0}}]]
g2=Graphics[Line[{{0,0},{15,15}}]]
g3=Graphics[{Opacity[0.2],Brown,Rotate[Rectangle[{8,8},{12,12}], 45 Degree, {Left, Bottom}]}]
g4=Graphics[{Blue, Thickness[0.01], Arrow[{{8,10.8}, {8,2.8}}]}]
g5=Graphics[{Cyan, Thickness[0.01], Arrow[{{8,10.8}, {3.8,15}}]}]
g6=Graphics[{Green, Thickness[0.01], Arrow[{{2.4,5.2}, {6.6,9.4}}]}]
g7 = Graphics[ Text[StyleForm["Weight", FontSize -> 14, FontWeight -> "Bold", FontColor -> Blue], {9.4, 6.8}, {0.4, 1}, {0, -1}]]
g8=Graphics[ Text[StyleForm["Normal", FontSize -> 14, FontWeight -> "Bold", FontColor -> Cyan], {6, 13}, {0, -1}, {1, -1}]]
g9=Graphics[ Text[StyleForm["Friction", FontSize -> 14, FontWeight -> "Bold", FontColor -> Green], {4.5, 7.2}, {0, 1}, {1, 1}]]
Show[g1,g2,g3,g4,g5,g6,g7,g8,g9]
     
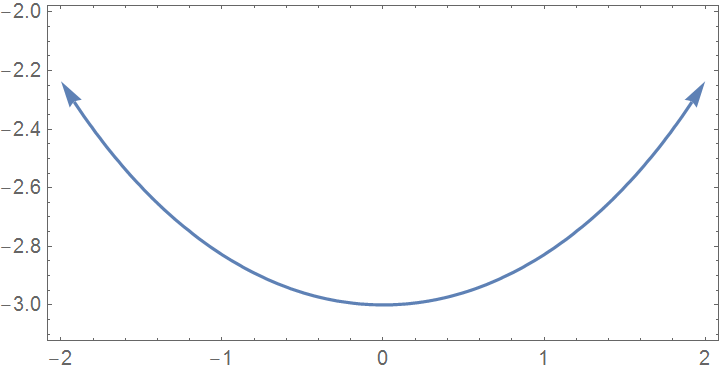
ContourPlot[x^2 + y^2 == 9, {x, -2, 2}, {y, -2, -3.1}, AspectRatio -> 0.5] /.
Line[x__] :> Sequence[Arrowheads[{-.04, .04}], Arrow[x]]
       Curve with arrows.            Mathematica code

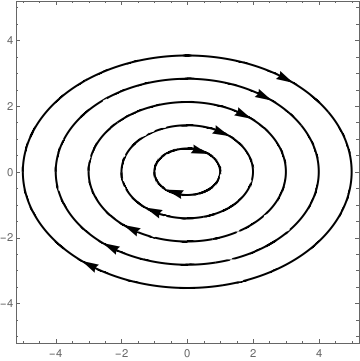
We can add arrows to multiple plots:

     
rules = {GraphicsComplex[x_, y_] :>
GraphicsComplex[SortBy[x, ArcTan[#[[1]], #[[2]]] + (\[Pi]/2) &],
y /. Line[pts_] :> {Arrowheads[{{-0.05, 1/8}, {-0.05, 5/8}}],
Arrow[pts]}]}
Show @@ Table[
ContourPlot[x^2 + 2*y^2 == r^2, {x, -r, r}, {y, -r, r},
PlotPoints -> 100, ContourShading -> False,
ContourStyle -> {Black, Thick}] /. rules, {r, 5, 1, -1}]
       Family of curves with arrows.            Mathematica code

To add uniform arrows to the graph, we use Alexey Popkov's completePlotRange for computing the actual PlotRange of a plot.

completePlotRange[plot : (_Graphics | _Graphics3D | _Graph)] :=
Last@Last@
Reap[Rasterize[
Show[plot, Axes -> True, Frame -> False,
Ticks -> ((Sow[{##}]; Automatic) &),
DisplayFunction -> Identity, ImageSize -> 0],
ImageResolution -> 1]]
     
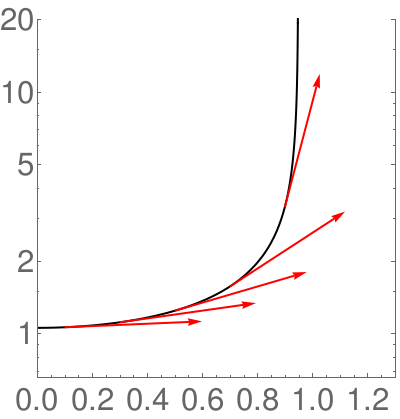
Block[{f, f0, df0, ar, plot}, f = (0.9 - x^2)^(-0.5);
f0 = Log[f] /. x -> x0;
df0 = D[Log[f], x] /. x -> x0;
plot = LogPlot[f, {x, 0, 1}, PlotRange -> {{0, 1.3}, {0.66, 20}},
Frame -> {{True, True}, {True, False}}, ImageSize -> 400,
PlotStyle -> {Directive[Black, Thick], Automatic},
BaseStyle -> {FontSize -> 30}, RotateLabel -> False,
AspectRatio -> 1];
ar = If[(AspectRatio /. Options[plot, AspectRatio]) === Automatic,
1, (AspectRatio /. Options[plot, AspectRatio])/
Ratios[Differences /@ completePlotRange@plot][[1, 1]]];
Show[plot, Graphics[{Red, Thick,
Table[Arrow[{{x0, f0}, {x0, f0} + 0.5 {1, df0}/Norm[{1, df0*ar}]}], {x0, 0.1, 0.9, 0.2}]}]]]
       Demonstration of Popkov's block.            Mathematica code

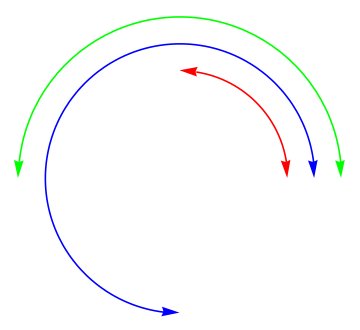
      Now we show how to plot figure when arrows are attached to curves/circles.
Show[ParametricPlot[#[[1]]*{Cos[θ], Sin[θ]}, {θ, #[[2]], #[[3]]},
Axes -> False, PlotStyle -> #[[4]]] /.
Line[x_] :> Sequence[Arrowheads[{-0.05, 0.05}], Arrow[x]] & /@
{{1, 0 Degree, 90 Degree, Red}, {1.25, 0 Degree, 270 Degree, Blue},
{1.5, 0 Degree, 180 Degree, Green}}, PlotRange -> All]
       Circles with arrows.            Mathematica code

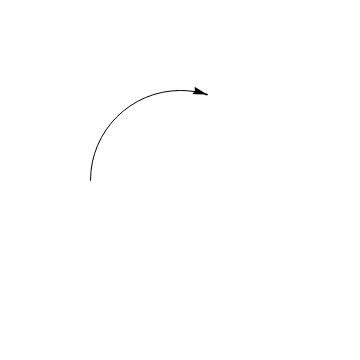
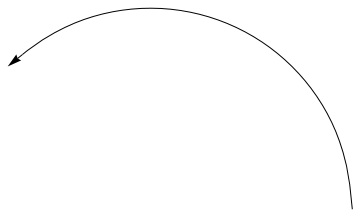
      Here is another block of codes with Manipulation option that allows you to change the size of arc.
start = \[Pi];
Manipulate[
Graphics[{Arrow[{{Cos[\[Theta] + If[\[Theta] < start, .01, -.01]],
Sin[\[Theta] + If[\[Theta] < start, .01, -.01]]}, {Cos[\[Theta]],
Sin[\[Theta]]}}], Circle[{0, 0}, 1, {start, \[Theta]}]},
PlotRange -> 2], {{\[Theta], .7 start}, 0, 2 start}]
      An arc with an arrow.            Mathematica code

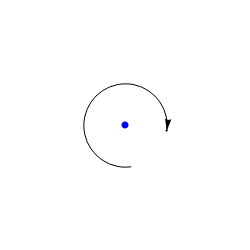
      When you need to see the center of the circle, use the folloiwng code:
Manipulate[
Graphics[{arcArrow[center, radius, {start, end}], PointSize[Large],
Blue, If[showCenter, Point[center]]}, PlotRange -> p,
ImageSize -> 250], {{start, \[Pi]/2}, -2 \[Pi], 2 \[Pi],
ImageSize -> Small}, {{end, 0}, -2 \[Pi], 2 \[Pi],
ImageSize -> Small}, {{radius, 1}, 1/2, 4,
ImageSize -> Small}, {{center, {0, 0}}, {-p, -p}, {p, p},
Slider2D}, {showCenter, {True, False}}, Initialization :> {p = 3;
arcArrow[a_, r_, {start_, end_}] := {Circle[a, r, {start, end}], Arrowheads[Medium],
Arrow[{a + r {Cos[end + If[end < start, .01, -.01]], Sin[end + If[end < start, .01, -.01]]}, a + r {Cos[end], Sin[end]}}]}}]
      An arc with an arrow and the center.            Mathematica code

Using Circle, define the function f (or whatever you want)
f[s_Circle] := s /. Circle[a_, r_, {start_, end_}] :> ({s, Arrow[{# - r/10^6 {-Sin@end, Cos@end}, #}]} &[ a + r {Cos@end, Sin@end}])
      Concave up:
Graphics@{Thickness[0.005], f[Circle[{0, 0}, 1, {4 Pi/3, 2 Pi}]]}

      Concave down:
Graphics@{Red, Thick, f[Circle[{0, 0}, 1, {- Pi/6, Pi}]]}

You can use Circle directly with anderfining procedure:
Unprotect[Circle]; Circle[a_: {0, 0}, r_: 1, {start_, end_}] := Block[{$inMsg = True}, {Circle[a, r, {start, end}], Circle[a, r, {start, end}] /. Circle[aa_, ar_, {astart_, aend_}] :> (Arrow[If[start < end, #, Reverse@#]] &@ {# - r/10^6 {-Sin@end, Cos@end}, #} & [aa + ar {Cos@aend, Sin@aend}])} ] /; ! TrueQ[$inMsg]; Protect[Circle];
Then plot two circle arcs in a row:
GraphicsGrid[{{Graphics@Circle[{0, 0}, 1, {2*Pi, 4*Pi/3}], Graphics@Circle[{0, 0}, 1, { 4*Pi/3, 2*Pi}]}}]
A function using a single ParametricPlot with multiple circles with arrows:
ClearAll[arcsWArrows];
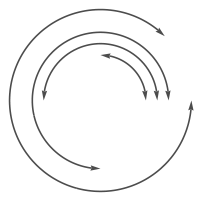
arcsWArrows[args1 : {{_, {_, _}} ..},
dir_List: {Directive[GrayLevel[.3],
Arrowheads[{{-0.05, 0}, {0.05, 1}}]]}] :=
ParametricPlot[
Evaluate[#[[1]]*{Cos[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]],
Sin[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]]} & /@ args1], {u, 0,
2 Pi}, PlotStyle -> dir, Axes -> False, PlotRangePadding -> .2,
ImageSize -> 200] /. Line[x_, ___] :> Arrow[x]
Then we use this function:
dsAndAngls = {{1, {0, \[Pi]/
2}}, {1.25, {0, \[Pi]}}, {1.5, {0, (3 \[Pi])/2}}, {2, {\[Pi]/
4, (4 \[Pi])/2}}};
directives = {Directive[Red, Thick,
Arrowheads[{{-0.05, 0}, {0.05, 1}}]],
Directive[Blue, Dashed, Arrowheads[{{-0.05, 0}, {0.05, 1}}]],
Directive[Green, Arrowheads[{{-0.05, 0}, {0.05, 1}}]],
Directive[Orange, Thickness[.02], Arrowheads[{{-0.07, 0}, {0.07, 1}}]]};

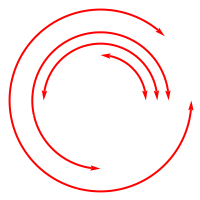
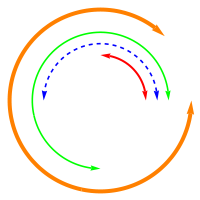
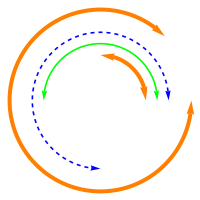
Row[{arcsWArrows[rdsAndAngls],
arcsWArrows[rdsAndAngls, {directives[[1]]}],
arcsWArrows[rdsAndAngls, directives],
arcsWArrows[rdsAndAngls, directives[[-1 ;; 2 ;; -1]]]}]
Another option gives Manipulate command:
Manipulate[ pts = N@Table[{Cos[k], Sin[k]}*r + o, {k, α Degree, β Degree, (β Degree - α Degree)/d}];
Show[
Graphics[{Lighter@Pink, AbsoluteThickness@10, Circle[o, r, {α Degree, β Degree}]}],
Graphics[{Arrow[pts, 0]}],
PlotRange -> {{-1.3, 1.3}, {-1.3, 1.3}}, AspectRatio -> 1,
Axes -> True, ImageSize -> 250 ],
{{d, 20, "res."}, 1, 100, Appearance -> "Labeled"},
{{α, 0, "α"}, 0, 360, Appearance -> "Labeled"},
{{β, 250, "β"}, 0, 360, Appearance -> "Labeled"},
{{r, 1, "r"}, 0.01, 2, Appearance -> "Labeled"},
{{o, {0, 0}, "origo"}, {-1, -1}, {1, 1}},
ControlPlacement -> Left ]
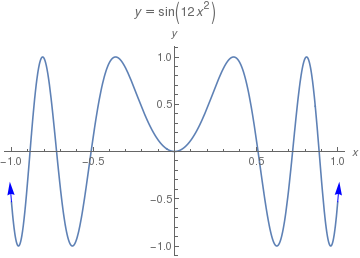
Next, we plot a simple curve that is generated by splines and is finished with arrow:
Graphics[Arrow[ BSplineCurve[Table[{Cos[x], Sin[x]}, {x, 0, Pi*3/4, Pi/20}]]]]

We plot a function that has the graph with ended arrows.

     
f[x_] := Sin[12 x^2]; xmin = -1; xmax = 1; small = .01;
Plot[f[x], {x, xmin, xmax}, PlotLabel -> y == f[x],
AxesLabel -> {x, y},
Epilog -> {Blue,
Arrow[{{xmin, f[xmin]}, {xmin - small, f[xmin - small]}}],
Arrow[{{xmax, f[xmax]}, {xmax + small, f[xmax + small]}}]}]
       Graph ends with arrows.            Mathematica code

 

Finally, we demontrate some examples of plotting with text and arrows.
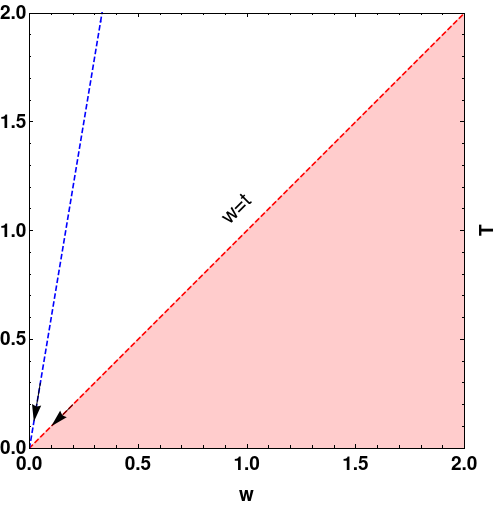
P1 = Plot[x, {x, 0, 2}, PlotStyle -> {Dashed, Red}, Filling -> Bottom]; P2 = Plot[6 x, {x, 0, 2}, PlotStyle -> {Dashed, Blue}]; Show[P1, P2, AspectRatio -> Automatic, Frame -> True, PlotRangePadding -> None, AxesOrigin -> {0, 0}, Axes -> None, FrameStyle -> Directive[Black], LabelStyle -> {18, Bold}, FrameLabel -> {{None, "T"}, {"w", None}}, ImageSize -> 500, Epilog -> { Arrow[{{.2, .2}, {.1, .1}}], Arrow[{.05 {1, 6}, {1, 6} .02}], Rotate[Text[Style["w=t", FontSize -> 20], {.95, 1.1}], Pi/4]}]
   Text with arrows using Plot       Mathematica code

Another example:

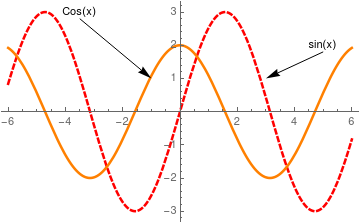
Plot[{3 Sin[x], 2*Cos[x]}, {x, -6, 6}, PlotStyle -> {{Thickness[0.007], Dashed, Red}, {Thickness[0.007], Orange}}, Epilog -> {{Arrow[{{5, 1.8}, {3, 1}}], Text["sin(x)", {5, 2}], Arrow[{{-3.5, 2.8}, {-1, 1}}], Text["Cos(x)", {-3.5, 3}]}}]
   Text with arrows using Plot       Mathematica code

     
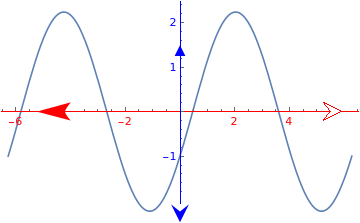
arrowhead1 = Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}}];
arrowhead2 = Polygon[{{-1.5833333333333333`, 0.4166666666666667`}, {-1.5410500000000003`, 0.369283333333333`}, {-1.448333333333333`, 0.255583333333333`}, {-1.3991000000000005`, 0.18721666666666673`}, {-1.3564666666666663`, 0.11826666666666673`}, {-1.3268499999999999`, 0.05408333333333341`}, {-1.3166666666666667`, 0.`}, {-1.3268499999999999`, -0.048950000000000195`}, \ {-1.3564666666666663`, -0.11228333333333372`}, {-1.3991000000000005`, \ -0.18353333333333333`}, {-1.448333333333333`, -0.2562833333333335`}, \ {-1.5410500000000003`, -0.38048333333333345`}, {-1.5833333333333333`, \ -0.43333333333333335`}, {0.`, 0.`}, {-1.5833333333333333`, 0.4166666666666667`}, {-1.5833333333333333`, 0.4166666666666667`}}];
arrowhead3 = Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}, {-0.6`, 0}, {-1, 0.5`}}];
arrowhead4 = {{FaceForm[GrayLevel[1]], Polygon[{{-0.6`, 0}, {-1.`, 0.5`}, {0.`, 0}, {-1.`, -0.5`}, {-0.6`, 0}}], Line[{{-0.6`, 0}, {-1.`, 0.5`}, {0.`, 0}, {-1.`, -0.5`}, {-0.6`, 0}}]}};
arrowhead5 = Polygon[{{-0.6582278481012658`, -0.43037974683544306`}, {0.`, 0.`}, {0.`, 0.`}, {0.`, 0.`}, {0.`, 0.`}, {0.`, 0.`}, {-0.6455696202531646`, 0.43037974683544306`}, {-0.4810126582278481`, 0.`}, {-0.6582278481012658`, -0.43037974683544306`}, \ {-0.6582278481012658`, -0.43037974683544306`}}];
Plot[2*Sin[x] - Cos[x], {x, -2 \[Pi], 2 \[Pi]},
AxesStyle -> {Directive[{Red,
Arrowheads[{{-0.06, 0.1(*Xleft*), {Graphics[{arrowhead}] /. arrowhead -> arrowhead2, 0.98`}}, {0.05,
0.95(*Xright*), {Graphics[{arrowhead}], 0.98`}}}] /. arrowhead -> arrowhead4}],
Directive[{Blue, Arrowheads[{{-0.05,
0(*Ydown*), {Graphics[{arrowhead}] /. arrowhead -> arrowhead3,
0.98`}}, {0.03, .8(*Yup*), {Graphics[{arrowhead}] /. arrowhead -> arrowhead1, 0.98`}}}]}]}]
       Demonstration of arrows.            Mathematica code

     
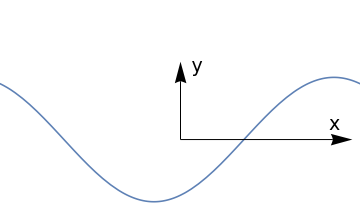
axes[x_, y_, f_, a_] :=
Graphics[Join[{Arrowheads[a]},
Arrow[{{0, 0}, #}] & /@ {{x, 0}, {0, y}}, {Text[
Style["x", FontSize -> Scaled[f]], {0.9*x, 0.2*y}],
Text[Style["y", FontSize -> Scaled[f]], {0.1 x, 0.95*y}]}]]

Show[Plot[1/2*Sin[x] - Cos[x], {x, -\[Pi], \[Pi]}, Axes -> None, PlotRange -> {{-Pi, Pi}, {-1.5, 2.5}}], axes[3, 1.4, 0.05, 0.06]]
       Figure with coordinate arrows.            Mathematica code

Plot with custom arrowheads:

     
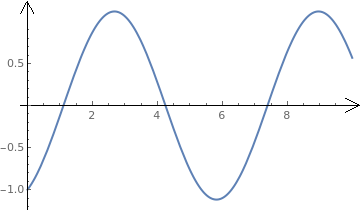
h = Graphics[Line[{{-1, 1/2}, {0, 0}, {-1, -1/2}}]];
Plot[1/2*Sin[x] - Cos[x], {x, 0, 10}, PlotStyle -> Thick,
AxesStyle -> Arrowheads[{{Automatic, Automatic, h}}]]
       Plot with custom arrowsheads.            Mathematica code

     
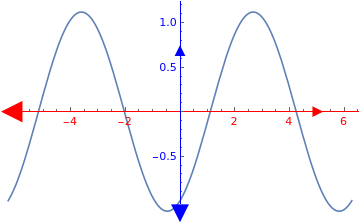
Plot[1/2*Sin[x] - Cos[x], {x, -2 \[Pi], 2 \[Pi]},
AxesStyle -> {Directive[{Red, Arrowheads[{{-0.06,
0(*Xleft*), {Graphics[{Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}}]}],
0.98`}}, {0.03, .9(*Xright*), {Graphics[{Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}}]}], 0.98`}}}]}],
Directive[{Blue,
Arrowheads[{{-0.05, 0(*Ydown*),
{Graphics[{Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}}]}],
0.98`}}, {0.03, .8(*Yup*), {Graphics[{Polygon[{{-1, 0.5`}, {0, 0}, {-1, -0.5`}}]}], 0.98`}}}]}]}]
       Plot with triangle arrowsheads.            Mathematica code

 

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)