Preface
A linear differential equation is an equation of the form \( y' + a(x)\,y = f(x) , \) where the coefficient a(x) and nonhomogeneous (also called forcing of driving) term are known continuous functions.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part II of the course APMA0330
Glossary
Linear Equations
A linear first order ordinary differential equation (ODE) can be used as a mathematical model for a variety of phenomena, either physical or non-physical. Examples of such phenomena include the following: heat flow problems (thermodynamics), simple electrical circuits (electrical engineering), force problems (mechanics), rate of bacterial growth (biological science), rate of decomposition of radioactive material (atomic physics), crystallization rate of a chemical compound (chemistry), and rate of population growth (statistics). Most of these problems, however, appear in systems of differential equations that are considered in the second course.
A differential equation, written in the normal form:
Theorem: Let a(x) and f(x) be continuous functions on the open interval (a,b), and let \( x_0 \in (a,b) . \) Then for each \( x \in (a,b) \) there exists a unique solution \( y = \phi (x) \) to the differential equation \( y' + a(x)\,y = f(x) \) that also satisfies the initial value condition that \( y(x_0 ) = y_0 \) for any real number y0. Moreover, this initial value problem has no singular solution. ■
Note that if the interval in the above theorem is the largest possible interval on which a(x) and f(x) are continuous, then the interval is the interval of validity for the solution. This means, that for linear first order differential equations, we won't need to actually solve the differential equation in order to find the largest possible interval where the solution exists and continuous (such interval is called the validity interval). Notice as well that the interval of validity will depend only partially on the initial condition. The interval must contain x0, but the value of y0 has no effect on the interval of validity.
Example: validity interval: Determine the validity interval for the initial value problem
Solution: First, in order to use the theorem to find the interval of validity, we must rewrite the differential equation in the normal form given in the theorem. So we need to divide out by the coefficient of the derivative.
Next, we need to identify where the two functions \( a(x) = \frac{3}{\left( x^2 -4 \right)} \) and \( f(x) = \frac{\ln |7-x|}{\left( x^2 -4 \right)} \) are not continuous. This will allow us to find all possible intervals of validity for the differential equation. So, a(x) is discontinuous at \( x= \pm 2 , \) while f(x) is also undefined at x = 7. Now, with these points in hand, we can break up the real number line into four intervals where both a(x) and f(x) will be continuous. These four intervals are,
Example: Consider the homogeneous linear equation
SolRule = DSolve[ode[x, y], y[x], x]
yh[x_] = Simplify[y[x] /. SolRule[[1]]] (* solution of the homogeneous eq *)
Simplify[ode[x, yh]] (* to check the answer *)
Integrating factor method allows us to reduce a linear differential equation in normal form \( y' + a(x)\,y = f(x) \) to an exact equation. There always exists an integrating factor μ(x) as a function of x:
The Bernoulli method suggests to seek a solution of the inhomogeneous linear differential equation (it does not matter whether the equation is in normal form or not) \( y' + a(x)\,y = f(x) \) in the form of the product of two functions:
Example: Consider the nonhomogeneous equation
SolnRule = DSolve[nde[x, y], y[x], x]
yn[x_] = Simplify[y[x] /. SolnRule[[1]]]
Its solution can be obtained in one line Mathematica code:
Now we apply the Bernoulli method: \( y(x) = u(x)\,v(x) , \) where u is a solution of the homogeneous equation
Example: Consider another example for a linear equation with variable coefficients:
y3[x_] = Simplify[y[x]/.SolxRule[[1]]]
Checking the answer:
We use an integrating factor method by solving the corresponding homogeneous/separable equation for μ(x):
Now we demonstrate the Bernoulli method: \( y(x) = u(x)\, v(x) , \) where u(x) is a solution of the homogeneous part \( x\, u' -5\,u =0 \) and v(x) is obtained upon solving the separable equation \( x\,u\, v' = 27\, x^7 \, e^x . \) Integrating these sequential equations
Example: Solve the IVP: \( 3ty' +2y=t^2 , \quad
y(1)=1 . \) We try to find its solution using Mathematica:
t0 = 1; y0 = 1;
p[t_] = 2/3/t; q[t_] = t/3;
P[t_] = Exp[Integrate[p[s], {s, t0, t}]];
y[t_] = 1/P[t]*(t0 + Integrate[P[u]*q[u], {u, t0, t}])
(Re[t] >= 0 || t \[NotElement] Reals) && (Re[u] >= 0 || u \[NotElement] Reals)]
Example: Using Mathematica, solve the linear differential equation: \( y' = e^{-2x} -3\,y , \)
and plot some its solutions.
gensol=DSolve[y'[x]==Exp[-2 x]-3 y[x],y[x],x]
In DSolve command, the first argument (y'[x]==Exp[-2 x]-3 y[x]) represents the differential equation,
the second argument (y[x]) instructs Mathematica that we are solving for y=y(x), and
the third argument (x) instructs Mathematica that the independent variable is x.
Note that gensol is a nested list. The first part of gensol, extracted with gensol[[1]], is the list (y(x)->E^(-2 x) + E^(-3 x) C[1]);
and the first part of this list, extracted with gensol[[1,1,1]], is y(x) while the second part of this list
(which represents the formula for the solution), extracted with gensol[[1,1,2]], is y=E^(-2 x) + E^(-3 x) C[1]
pp=Plot[Evaluate[toplot],{x,-1/2,1},PlotRange->{-3/4,3/4},AspectRatio->1,
AxesStyle->GrayLevel[0.5],PlotStyle->{{GrayLevel[0.4],Thickness[0.01]}}, AxesLabel->{x,y}]

Axes -> Automatic, VectorScale -> (1 &), AxesOrigin -> {0, 0}, VectorStyle -> Arrowheads[0]]


Example:In mining, “mine tailing” are what is left after everything valuable (such as a mineral, coal, or oil) has been removed. The material that is left over after the minerals, coal, or oil is extracted often presents a great deal of hazard to the environment. One of the ways of processing mine tailing is to store them in a pong; this method is commonly used when water is used in the mining extraction. This method allows any particles that are suspended in the water to settle at the bottom of the pond. The water can then be treated and recycled.
Suppose that we have a gold mining operation and we are storing our tailing in a pond that has an initial volume of 100,000 cubic meters. When we begin our operation, the pond is filled with clean water. The pond has a stream flowing into it, and water is also being pumped out of the pond. Chemicals are used as a way to process gold ore, which is the material being extracted in this operation. Chemicals that are used, like sodium cyanide, are often highly poisonous and harmful to the environment. Thus, the water must be treated before it is released into the watershed. Suppose that 3,000 cubic meters per day flow into the pond from stream, and 3,000 cubic meters are pumped out of the pond each day to be processed and recycled. Since inflow and outflow are equal, the water level of the pond remains constant.
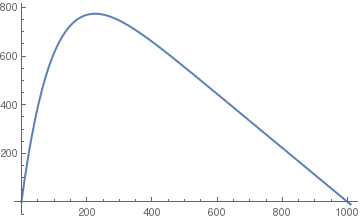
At time t=0, the water from stream becomes contaminated with chemicals from the mining operation at a rate of 10 kilograms of chemicals per 1000 cubic meters. We will assume that water in our tailing pond is well mixed so that the concentration of chemicals throughout the pond is uniform. In addition, any matter pumped into the pond from the stream settles to the bottom of the pond at a rate of 100 cubic meters per day. Thus, the volume of the pond is reduced by 100 cubic meters each day, and will become full after 500 days of operation. We shall assume that the particulate matter and the chemicals are included in the 1000 cubic meters that flow into the pond from the stream each day.
We want to find a differential equation that will model the amount of chemicals in the tailing pond at any particular time. Let y(t) be the amount of chemicals in the pond at time t. Then \( {\text d}y/{\text d}t \) is the difference between the rate at which the chemicals enter the pond and the rate at which the chemicals leave the pond.
Since water flows into the pond from the stream at a rate of 1000 cubic meters per day, the rate as which the chemicals enter the pond is 10 kilograms per day. On the other hand, the rate at which the chemicals leave the pond will depend on the amount of chemicals in the pond at time t. The volume of the pond is decreasing due to sediment, and at time t it is V(t)=100000−100t. Thus, the concentration of chemicals in the pond at time t is y/(100000−100t), and the rate at which the chemicals are flowing out of the pond to be recycled is
Notice that the above equation is not autonomous. In fact, it is not even separable. We will have to use a different approach to find a solution. First, we will rewrite the equation in the form suitable for an integrating factor
Plot[f[t], {t, 0, 1009}, PlotStyle -> Thick]
Example: Mixing Models. Many applications involve the mixing of two or more substances together. We can model how petroleum products are mixed together in a refinery, how various ingredients are mixed together in a brewery, or how greenhouse gases mix and move across various layers of the earth's atmosphere. Basically, it consists of finding a formula for the amount of some "pollutant" in a container, into which pollutant is entering at a fixed rate and also flowing out at a fixed rate. The general physical rule used to describe this situation is
Suppose that a 400-liter tank initially contains 200 liters of salt water containing 2 kilograms of salt. A brine mixture containing 1/10 kilograms of salt per liter flows into the top of the tank at a rate of 4 liters per minute. A well-mixed solution leaves the tank at rate of 3 liters per minute. We wish to know how much salt is in the tank, when the tank is full.
To construct our model, we will let t be the time (measured in minutes) and set up a differential equation that will measure how fast the amount of salt at time t, y(t), is changing. We have the initial condition y(0) = 5, and
Example: gas in magma affects volcanic eruptions. Many andesitic volcanoes exhibit effusive eruption activity, with magma volumes as large as 107 -- 109 m3 erupted at rates of 1 -- 10 m3/s over periods of years or decades. During such eruptions, many complex cycles in eruption rates have been observed, with periods ranging from hours to years. Longerterm trends have also been observed, and are thought to be associated with the continuing recharge of magma from deep in the crust and with waning of overpressure in the magma reservoir. Here we present a model which incorporates effects due to compressibility of gas in magma. The eruption duration and volume of erupted magma may increase by up to two orders of magnitude if the stored internal energy associated with dissolved volatiles can be released into the magma chamber. This mechanism would be favored in shallow chambers or volatile-rich magmas and the cooling of magma by country rock may enhance this release of energy, leading to substantial increases in eruption rate and duration.
Consider a magma with bulk density ρ in a chamber of volume V undergoing a mass recharge rate Qi and eruption rate Q0. Conservation of mass indicates that
It is known that the rate of change in volume of the chamber, \( {\text d}V / {\text d}t , \) is related to the associated rate of change in pressure, \( {\text d}p / {\text d}t , \) as a result of deformation of the surrounding rock by:
Although the initial equation has partial derivatives, it can be assumed for the sake of this model that temperature is constant throughout the eruption thus the equation can be simplified to an ODE and solved both numerically and analytically.
Herbert E. Huppert & Andrew W. Woods.,
The role of volatiles in magma chamber dynamics,
nature, Vol 420, 493--495, 2002.
Example: adding milk to coffee. Usually, there is a gap in time between you drink coffee and add cold mild to hot coffee. The temperature inside a mug of coffee is governed by the Newtons's equation.
{
sols = NDSolve[{
D[Temp[t], t] == -0.1 (Temp[t] - ambient),
Temp[0] == beginTemp,
WhenEvent[
t > addMilk,
Temp[t] -> (coffee*Temp[t] + milk*milkTemp)/(coffee + milk)]},
Temp, {t, 0, experimentTime} ];
Plot[
Temp[t] /. sols, {t, 0, experimentTime},
PlotRange -> {{0, experimentTime}, {0, beginTemp + 10}},
AxesLabel -> {"Time (minutes)", "Temperature ˚C"},
LabelStyle -> Directive[Bold, Medium],
ImageSize -> {{400, 600}}]
},
{{ambient, 20, "Ambient temperature"}, 0, 30, 0.5, Appearance -> "Labeled"},
{{experimentTime, 30, "Time of Experiement(minutes)"}, 1, 100, 0.5, Appearance -> "Labeled"},
{{beginTemp, 80, "Coffee start temperature"}, 50, 100, 0.5, Appearance -> "Labeled"},
{{milkTemp, 5, "Milk start temperature"}, 1, ambient, 0.5, Appearance -> "Labeled"},
{{addMilk, 1, "Time to add milk(minutes)"}, 1, 100, 1, Appearance -> "Labeled"},
{{coffee, 200, "Coffee volume (ml)"}, 100, 500, 10, Appearance -> "Labeled"},
{{milk, 20, "Milk volume (ml)"}, 0, 50, 5, Appearance -> "Labeled"}, ControlPlacement -> Left
]
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)