Preface

This section is devoted to the backward Euler method.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part III of the course APMA0330

Glossary

Backward Euler method

Suppose that we wish to numerically solve the initial value problem
\[ y' = f(x,y), \qquad y(x_0 ) = y_0 , \]
where y' = dy/dx is the derivative of function y(x) and (x0,y0) is a prescribed pair of real numbers. We assume that f is a smooth function so that the given initial value problem has a unique solution. We seek a numerical solution on the interval [𝑎,b], where we usually set x0 = 𝑎. Subdivide the interval [𝑎,b] with N+1 mesh points x0, x1, … , xN with x0 = 𝑎, xN = b. Let h = (b - 𝑎)/N be the step size, so that xn = 𝑎 + hn, n = 1, 2, … , N. In some problems h is given, then N = (b - 𝑎)/h. Integrating the given differential equation, we come to the integral equation
\[ y(x) = y(a) + \int_a^x f(t, y(t))\,{\text d}t \]
Now we set x = xn in the above equation and break the integral into the sum of integrals over each subinterval [xn,xn+1]. This leads to the sequence of integral equations for each subinterval:
\[ y \left( x_n \right) = y \left( x_{n-1} \right) + \int_{x_{n-1}}^{x_n} f(t, y(t))\,{\text d}t, \qquad n= 1,2,\ldots , N, \]
where y0 = y(𝑎), which is given. Note that y(xn) are unknown for n = 1, 2, … , N. s usual, we denote by yn the approximate values of y(xn) at mesh points. Using the simple right rectangular rule for the approximation of the integral (that is, when the integrand is evaluated at the right end point) would lead to
\[ \int_{x_{n-1}}^{x_n} f(t, y(t))\,{\text d}t \approx f \left( x_n , y(x_n )\right) \left( x_n - x_{n-1} \right) , \qquad n= 1,2,\ldots , N. \]
This yields the backward Euler formula
\[ y_{n+1} = y_n + h\, f(x_{n+1}, y_{n+1}) , \qquad y_0 = y(0), \qquad n=0,1,2,\ldots . \]
   
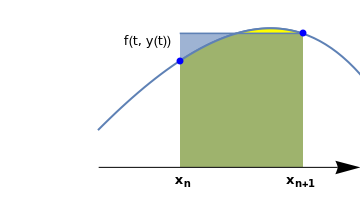curve=Plot[x-Exp[x-0.05]+1.5,{x,-1.0,0.7},PlotStyle->Thick,Axes->False,Epilog->{Blue,PointSize@Large,Point[{{-0.5,0.42},{0.25,0.53}}]},PlotRange->{{-1.6,0.6},{-0.22,0.66}}];
line=ListLinePlot[{{-0.5,0.53},{0.25,0.53}},Filling->Bottom,FillingStyle->Opacity[0.6]];
curve2=Plot[x-Exp[x-0.05]+1.5,{x,-0.5,0.25},PlotStyle->Thick,Axes->False,PlotRange->{{-1.6,0.6},{0.0,0.66}},Filling->Bottom,FillingStyle->Yellow];
ar1=Graphics[{Black,Arrowheads[0.07],Arrow[{{-1.0,0.0},{0.6,0.0}}]}];
t1=Graphics[Text[Style["f(t, y(t))",FontSize->12],{-0.7,0.5}]];
xn = Graphics[ Text[Style[Subscript["x", "n"], FontSize -> 12, FontColor -> Black, Bold], {-0.48, -0.05}]];
xn1 = Graphics[ Text[Style[Subscript["x", "n+1"], FontSize -> 12, FontColor -> Black, Bold], {0.24, -0.05}]];
Show[curve,curve2,line,ar1,t1,xn,xn1]

The backward Euler formula is an implicit one-step numerical method for solving initial value problems for first order differential equations. It requires more effort to solve for yn+1 than Euler's rule because yn+1 appears inside f. The backward Euler method is an implicit method: the new approximation yn+1 appears on both sides of the equation, and thus the method needs to solve an algebraic equation for the unknown yn+1. Frequently a numerical method like Newton's that we consider in the section must be used to solve for yn+1. The backward Euler method is also a one-step method similar to the forward Euler rule.

Here is a Mathematica code to perform the backward Euler rule:

backeuler[{x0_, xn_}, {y0_}, steps_] :=
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
s = FindRoot[ynew == yold + h*f[xnew, ynew], {ynew, yold}];
yn = ynew /. s;
sollist = Append[sollist, {xnew, yn}];
xold = xnew; yold = yn, {steps}];
Return[sollist]]
which we apply to determine the numerical approximations at grid points:
f[x_, y_] = y^2 - x^2
backeuler[{0, 1}, {1/2}, 10]
The above Mathematica scripts were applied to numerically solve the initial value problem: y' = y² - x²,   y(x0) = y0, for demonstration.

NSolve has to spend time to compute all roots to the equation (which can be computationally expensive). FindRoot does a pretty fast search looking for only a single root, so it is quick for complex equations.
If you care about all possible roots, or if you have no clue where the roots of the equation may be, FindRoot is a terrible choice. If you only care about a single root and have a rough idea of where it might be, though, FindRoot will find it quickly. Therefore, we use only this command in the backward Euler formula.

Example: Consider the initial value problem for the linear equation

\[ \frac{{\text d}y}{{\text d}x} = x\,y - x^2 , \qquad y(0) = 1. \]
The results of applying Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

Example: Consider the initial value problem for the logistic equation

\[ \frac{{\text d}y}{{\text d}t} = y\left( 3 - y \right) , \qquad y(0) = 1. \]
The results of applying Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

Example: Consider the initial value problem \( y'= 1/(3x-2y+1),\quad y(0)=0 \)

The results of applying Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

Example: Consider the following initial value problem:

\[ y' = y^3 - 3\,t , \qquad y(0) =1 . \]
Here is the Mathematica code that solve this problem:
y[0] = 1.;        (* initial condition *)
h = 0.1;          (* step size *)
t[0] = 0.;        (* starting value of the independent value *)
M = Round[0.5/h];       (* number of points to reach the final destination, in our case it is 0.5    *)
toler = h;      (* define the tolerance *)
Do[
  t[n + 1] = t[n] + h;
  eqn = (z == y[n] + h (z^3 - 3 t[n + 1]) );
  ans = z /. NSolve[eqn, z, Reals];
  indlist = {};
  toler = h;
 While[ Length[indlist] == 0, 
  toler = toler*2.;
  indlist = Flatten[Position[Map[(Abs[y[n] - #] < toler) &, ans], True]];
  ];
  ind = indlist[[1]];
  y[n + 1] = ans[[ind]];
  , {n, 0, M}]

Then we plot the solution:
ListPlot[Table[{t[n], y[n]}, {n, 0, M}], PlotStyle->PointSize[0.025]]
y[M]
t[M]

The results of applying Euler's rule with h = 0.1
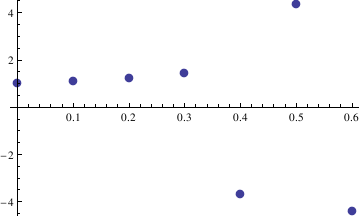
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

 

Central Difference Scheme

However, this is not the only approximation possible, one may consider the central difference:
\[ y' (x_n ) \approx \frac{y_{n+1} - y_{n-1}}{2h} , \]
which usually gives a more accurate approximation. Using central difference, we get a two-step approximation:
\[ y_{n+1} = y_{n-1} + 2h\, f\left( x_n , y_n \right) , \qquad n=1,2,\ldots , \]
which requires two starting points to solve this recurrence of second order. So one can use standard Euler rule to determine y1: \( y_1 = y_0 + h\, f\left( x_0 , y_0 \right) . \) However, this numerical algorithm may produce instability and we may observe a numerical solution that is different from the true solution. Such solution is called a "ghost solution." This phenomenon is caused by roundoff errors.

Example: We consider the following initial value problem for the Riccati equation

\[ y' = y^2 - x^2 , \qquad y(0) = 1/2 . \]
The results of applying Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

 

Nonstandard Euler Methods

Let ϕ be a real-valued function on ℝ that satisfies the property:

\[ \phi (h) = h + O\left( h^2 \right) \qquad\mbox{and} \qquad 0 < \phi(h) < 1 \quad\mbox{for all positive $h$}. \]
There exists a variety of functions φ that satisfy the above condition, e.g., \( \phi (h) = 1 - e^{-h} \quad \Longrightarrow \quad \phi (hq)/q = \left( 1- e^{-hq} \right) /q . \) Then the following nonstandard schemes are stable:

Example: Consider the initial value problem

\[ y' = 50\,x - 50\,y -1, \qquad y(0) = 1. \]
The solution of this problem is
DSolve[{y'[x] == 50*x - 50*y [x] - 1, y[0] == 1}, y, x]
\[ y(x) = \frac{26}{25}\, e^{-50\,x} - \frac{1}{25} + x . \]
The results of applying forward Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
The results of applying backward Euler's rule with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
The results of applying nonstandard scheme with h = 0.1
n xn yn Exact solution Absolute error
1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7
8 0.8
9 0.9
10 1.0
   ■

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)