Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part I of the course APMA0330

Glossary

Preface

This section is devoted to aspects of qualitative analysis of first order differential equations in normal form. Other properties of the solution such as bounds, asymptotic expansions, stability, periodicity, etc., without explicitly solving the equation, will be explored later.

Qualitative Analysis

For a differential equation \( y' = f(t,y) , \) subject to some initial condition, we may want to know what happens to the solution y(t) when t is very large. The solution may approach some curve or straight line, may be periodic or exhibiting some kind of oscillations. In the second tutorial, we will meet chaotic solutions that do not approach any pattern. To answer this question, there are four methods to be used and discussed. If we can find a formula for y(t), we may accept \( \lim_{t\to \infty} y(t) \) for an answer. Most likely, we do not have a formula (even implicit), we can try a numerical computation for large values of t to get some idea of what happens, the drawback being that accuracy may deteriorate significantly over a long x interval. Hence, this approach is unreliable. With a computer algebra system, one may try to plot direction fields for different regions, but this geometric description of the solutions may lead to wrong conclusions because you never know when the solution changes its mind. Therefore, we need to rely on methods that allow one to determine the behavior of solutions without actual attempt to find or estimate its values.

When we model a practical phenomena, a physical system in perfect balance may be difficult to achieve(a coin standing on the edge) or easy to maintain (when you part your car). So behavior of a system can be hard to predict except some simple cases when we know the answer (oscillating pendulum). When a solution of the differential equation approaches a perfect balance, we say that it is coming to an equilibrium position. In this section, we discuss such behavior mostly for autonomous differential equations.

The nullclines of the differential equation y' = f(t,y) are curves of zero inclination that are defined as solutions of the equation f(t,y) = 0.
Nullclines are usually not solutions of the differential equation unless they are constants. The solution curves may cross nullclines when their slope is zero.

Point equilibria (or critical point) of an autonomous differential equation \( {\text d}y / {\text d} t = f(y) \) are defined as the solutions of f(y) = 0. Solutions of this algebraic equation are the constant solutions of the given differential equation. If y* is a point equilibrium of the differential equation \( \dot{y} = f(y) , \) and all solutions starting near it, stay nearby for all t, then we call it locally stable. When these solutions also approach the equilibrium point, then it is called asymptotically stable. Otherwise we call y* unstable. If solutions approach the critical point from one side, but depart from another side, then such equilibrium solution is called semi-stable. If all solutions approach the critical point whenever they start, then such equilibrium is called globally stable.
The constant equilibrium solutions to an autonomous ordinary differential equation play a distinguished role because they may not appear in the general solution formula (even when arbitrary constant approaches infinity). There is a graphical and an analytical way to determine stability.
Theorem: Suppose that y* is an equilibrium of the autonomous differential equation dy/dt = f(y) for some smooth slope function f.
  • If the derivative of the slope function at the critical point is negative, f(y*) < 0, then the equilibrium solution is asymptotically stable.
  • If the derivative of the slope function at the critical point is positive, f(y*) > 0, then the equilibrium solution is unstable.
  • If the derivative of the slope function at the critical point is zero, f(y*) = 0, then this test is inconclusive and the behavior of the solutions depends on the nonlinear terms.
A critical point y* is stable or unstable depending on the behavior of solutions of the differential equation
\[ \dot{y} = \frac{{\text d}y}{{\text d}t} = f(y), \qquad \mbox{with } f\left( y^{\ast} \right) =0, \]
near the equilibrium. Assuming that the solution y(t) of the given autonomous differential equation is near the equilibrium point, at least initially for t ∈ [0,T] for some positive real number T. Then we expand the slope function into Taylor's series
\[ f(y) = f\left( y^{\ast} \right) + f' \left( y^{\ast} \right) \left( y - y^{\ast} \right) + \frac{1}{2!}\, f'' \left( y^{\ast} \right) \left( y - y^{\ast} \right)^2 + \cdots = f' \left( y^{\ast} \right) \left( y - y^{\ast} \right) + \cdots . \]
Replacing the slope function by its linearization, we obtain
\[ \dot{y} = f' \left( y^{\ast} \right) \left( y - y^{\ast} \right) , \]
which is valid for t ∈ [0,T]. The omitted terms in the above differential equation can be considered as a small pertubation. The obtained linear differential equation is actually quite simple and its solution becomes
\[ y(t) = y^{\ast} + C\, e^{f' \left( y^{\ast} \right) t} , \]
for some constat C. If f(y*) > 0, then the exponential term blows up when t

Example: Consider the autonomous differential equation: \( y'= y^2 \) subject \( y(t_0) = y_0 = 2. \) Separating the variables, we get

\[ \frac{{\text d}y}{y^2} = {\text d}x\qquad \Longrightarrow \qquad -\frac{1}{y} = x+C , \]
where C is an arbitrary constant. From the initial condition, we find
\[ y(x) = \frac{y(t_0 )}{1 - y(t_0 ) \left( t - t_0 \right)} = \frac{2}{1-2x} , \]
when the initial condition is taken as \( y(0) = 2. \) So C = 1/2. As t approaches the critical value \( t^{\ast} = t_0 + 1/y(t_0 ) \) from below, the solution blows up, meaning y(t) ↦ ∞ as t → t*. The blow-up time t* depends upon the initial data---the larger y0 > 0 is, the sooner the solution goes off to infinity. If the initial data is negative, y0 < 0, the solution is well-defined for all t > t0, but has a singularity in the past, at \( t^{\ast} = t_0 + 1/y(t_0 ) < t_0 . \) The only solution that exists for all positive and negative time is the constant solution y(t) ≡ 0, corresponding to the initial condition y(t0) = 0.

The above conclusion becomes obvious for our particular case: t0 = 0 and y0 = 2. So, a continuous solution also exists on the interval \( (-\infty , 1/2) . \) If we change initial condition \( y(0) =-1 , \) the explicit solution becomes

\[ y(t) = -\frac{1}{1+t} . \]
Hence, a continuous solution exists on \( (-1, \infty ) . \)

Upon plotting its direction field, we see that y = 0 is so called semi stable equilibrium solution because solutions started in negative semi-line approach y = 0 while solutions having positive initial conditions depart from the equilibrium solution.

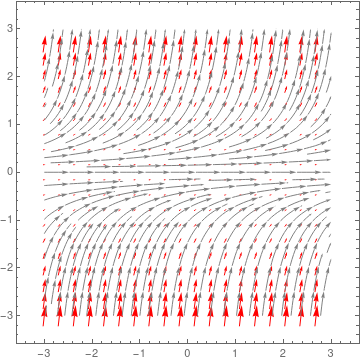
StreamPlot[{1, y^2}, {x, -3, 3}, {y, -3, 3}, PerformanceGoal -> "Quality", StreamPoints -> Fine, StreamStyle -> Gray, VectorPoints -> 20, VectorStyle -> {Arrowheads[4], Red}]
   Phase portrait for y' = y²       Mathematica code
As it is seen from the direction field, a small perturbation from the equilibrium solution y = 0 causes a dramatic change in the behavior of the solution: it becomes unbounded. On the other hand, a 1% change in the input function \( y' = y^2 + 0.01 \) with the same initial condition leads to complete different solution, which is a periodic one:
\[ y(t) = \frac{1}{10}\, \tan \left( \frac{t}{10} + \arctan \left( 10\,y(0) \right) \right) . \]
   ■

Example: Consider the not autonomous differential equation: \( y'= \left( 1- 3t \right) y^2 \) subject \( y(t_0) = y_0 = 2. \) Separating the variables, we get

\[ \frac{{\text d}y}{y^2} = \left( 1 - 3t \right) {\text d} t \qquad \Longrightarrow \qquad - \frac{1}{y} = t - \frac{3}{2}\, t^2 + C . \]
Solving for y, we obtain
\[ y(t) = \frac{2\, y(t_0 )}{2 - 2\,t\,y(t_0 ) + 3\,t^2 y(t_0 ) + 2t_0 \,y(t_0 ) - 3\, t_0^2 y(t_0 )} . \]
Upon plotting the direction field, we see that the equilibrium solution y(t) ≡ 0 is semistable.
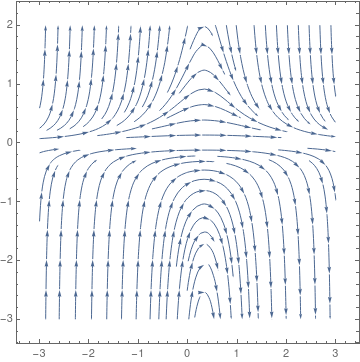
StreamPlot[{1, (1 - 3*t)*y^2}, {t, -3, 3}, {y, -3, 3}, StreamScale -> 0.15]
Solve[-1/y == t-3/2*t^2 -1/y0 -t0 +3/2*t0^2, y]
{{y -> (2 y0)/(2 - 2 t y0 + 3 t^2 y0 + 2 t0 y0 - 3 t0^2 y0)}}
   Phase portrait for y' = (1-3t)y²       Mathematica code
   ■

Example: Consider the autonomous differential equation

\[ \dot{y} = \left( y^2 -1 \right) \left( y+2 \right)^2 . \]
Upon plotting its direction field
StreamPlot[{1, (y*y - 1)*(y + 2)*(y + 2)}, {t, 0, 4}, {y, -4, 3}, StreamScale -> 0.12]
Direction field for the equation y' = (y² -1)(y + 2)²

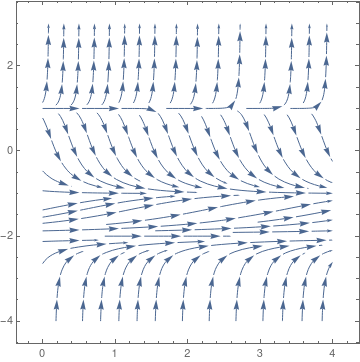
we conclude that y = 1 is unstable critical point and y = -1 is asymptotically stable equilibrium solution. However, y = -2 behaves differently from either of these two. Solutions that start below it move towards y = -2 while solutions that start above y = -2 move away as t increases. In cases where solutions on one side of an equilibrium solution move towards the equilibrium solution and on the other side of the equilibrium solution move away from it we call the equilibrium solution semi-stable. So y = -2 is a semi-stable equilibrium solution.    ■

For the graphical analysis, we plot f(y) as a function of y. The points equilibria are the points of intersection of the graph f(y) with the horizontal axis. To determine stability, we check how solutions behave in a neighborhood of each point equilibrium. Plotting a direction field or phase portrait would be helpful.

The analytical analysis is based on linearization of the slope function about the equilibrium. The linearization of f(y) about the equilibrium y* is

\[ f(y) = f \left( y^{\ast} \right) + f' \left( y^{\ast} \right) \left( y- y^{\ast} \right) + \cdots . \]
A perturbation about the equilibrium y* can be written as \( z= y - y^{\ast} . \) Now, since \( \frac{{\text d}z}{{\text d}t} = \frac{{\text d}y}{{\text d}t} , \) we find
\[ \frac{{\text d}z}{{\text d}t} = f' \left( y^{\ast} \right) z \]
for z sufficiently small. Comparing this with exponential growth, it follows that y* is locally stable if \( f' \left( y^{\ast} \right) < 0 , \) and unstable if \( f' \left( y^{\ast} \right) > 0 . \) When \( f' \left( y^{\ast} \right) = 0 , \) the linear stability analysis is inconclusive. The analytical approach agrees with the graphical analysis: At locally stable equilibria, the slope of the tangent line at the equilibrium is negative; if the equilibrium is unstable, it is positive.

 

Some applications in population modeling

Although population models will be analyzed later in special section, we touch this topic now to demonstrate qualitative behavior of corresponding solutions. When the size of population is big, it makes sense to describe their populations by continuous functions despite that in reality we deal with discrete quantities---people, animals, or bacteria. As first proposed by the English economist Thomas Malthus in 1798, the population of a species grows, roughly, in proportion to its size
\[ \frac{{\text d}P}{{\text d}t} = r\,P(t) , \]
where P(t) is the population of particular species at time t and the proportionality factor r measures the rate of growth, namely the difference between the birth rate and the death rate.

In the very simplest and not realistic model, the growth rate r is assumed to be independent of the population size P and time t. Then its solution exhibits the Malthusian exponential growth law

\[ P(t) = P\left( t_0 \right) e^{r(t- t_0 )} . \]
If r > 0, the population grows without limit, while if r < 0, the population dies out, so P(t) ↦ 0 as t → ∞, at an exponentially fast rate. The Malthusian population model provides a reasonably accurate description of the behavior of an isolated population in an environment with unlimited resources.

In a more realistic scenario, the growth rate will depend upon the size of the population as well as external environmental factors, including seasonable impact. For example, in the presence of limited resources, large population will have insufficient resources to increase. In other words, the growth rate r(P) > 0 when P < K, while r(P) < 0 when P > K, where the carrying capacity (or saturation level) K > 0 depends upon the resource availability. The simplest class of functions that satisfies these two inequalities are of the form

\[ \frac{{\text d}P}{{\text d}t} = r\,P(t) \left( 1 - \frac{P(t)}{K} \right) . \]
This model assumes that the environment is not changing over time and it is called the logistic equation by the Belgian mathematician Pierre F. Verhulst (1804--1849). Here constant r is called the intrinsic growth rate---that is, the growth rate in the absence of any limiting factors. Equating the slope function to zero,
\[ r\,P(t) \left( 1 - \frac{P(t)}{K} \right) =0, \]
we find two equilibrium (constant) solutions: \( P = \phi_1 (t) \equiv 0 \) and \( P = \phi_2 (t) \equiv K . \) The zeros of the slope function are also called the critical points or stationary solutions. To visualize other solutions of the logistic equation and to sketch their graphs, we draw the slope function f(P). It is clear that f(P is a parabola with the vertex at (K/2 , rK/4). the derivative \( {\text d}P/{\text d}t = f(P) = rP(1-P/K) \) is positive for 0 < P < K; Therefore, P is an increasing function of t when P is in this interval; we indicate this situation by the rightward-pointing arrows near the P-axis. Similarly, if P > K, then \( {\text d}P/{\text d}t = f(P) = rP(1-P/K) \) is negative; hence, P is decreasing, as indicated by the leftward-pointing arrow.
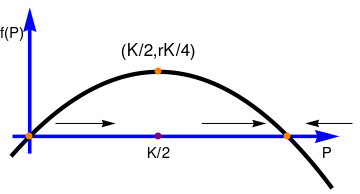
pp = Plot[P*(1-P/3), {P,-0.2,3.5}, PlotStyle->{Thickness[0.012], Black}, Axes->False]
axes1 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{-0.2,0},{3.6,0}}]}]
axes2 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{0,-0.2},{0,1.5}}]}]
p0 = Graphics[{PointSize[Large], Orange, Point[{0,0}]}]
p3 = Graphics[{PointSize[Large], Orange, Point[{3,0}]}]
p = Graphics[{PointSize[Large], Orange, Point[{3/2,3/4}]}]
p2 = Graphics[{PointSize[Large], Purple, Point[{3/2,0}]}]
ar1 = Graphics[Arrow[{{0.3,0.15},{1,0.15}}]]
ar2 = Graphics[Arrow[{{2.0,0.15},{2.75,0.15}}]]
ar3 = Graphics[Arrow[{{3.75,0.15},{3.2,0.15}}]]
txt1 = Graphics[Text[Style["K/2", FontSize -> 14, Black], {3/2, -0.2}]]
txt2 = Graphics[Text[Style["(K/2,rK/4)", FontSize -> 14, Black], {3/2, 1}]]
txt3 = Graphics[Text[Style["f(P)", FontSize -> 14, Black], {-0.2, 1.2}]]
txt4 = Graphics[Text[Style["P", FontSize -> 14, Black], {3.46, -0.2}]]
Show[axes1,axes2,pp,p0,p,p2,p3,ar1,ar2,ar3,txt1,txt2,txt3,txt4]
   Graph of f(P)       Mathematica code

In this context the P-axis is often called the phase line, and it is reproduced in is in its more customary vertical orientation in the figure. The dots at P = 0 and P = K are the critical points, or stationary solutions. The arrows again indicate that P is increasing whenever 0 < P < K and that P is decreasing whenever P > K. Note that is P is near zero or K, then the slope f(P) is near zero, so the solution curves are relatively flat. They become steeper as the value of P leaves the neighborhood of zero or K.

Then we plot the direction field using Mathematica command StreamPlot:

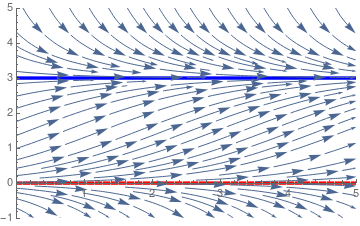
a = Plot[0, {t, 0, 4}, PlotStyle -> {Thickness[0.01], Dashed, Red}, PlotRange -> {{0, 4}, {-1, 5}}]
b = Plot[3, {t, 0, 4}, PlotStyle -> {Thickness[0.01], Blue}, PlotRange -> {{0, 4}, {-1, 5}}]
sp = StreamPlot[{1, P*(1 - P/3)}, {t, 0, 4}, {P, -1, 5}, StreamScale -> 0.12]
Show[a, b, sp]
a1 = Graphics[Arrow[{{0,-0.2}, {0,3.55}}]]
a2 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{0,0.2}, {0,2.9}}]]
a3 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{0,3.5}, {0,3.1}}]]
p21 = Graphics[{PointSize[Large], Purple, Point[{0,3}]}]
p22 = Graphics[{PointSize[Large], Purple, Point[{0,0}]}]
Show[a1,a2,a3,p21,p22]
   Phase portrait for the logistic equation       Mathematica code

 

If we modify the logistic equation as
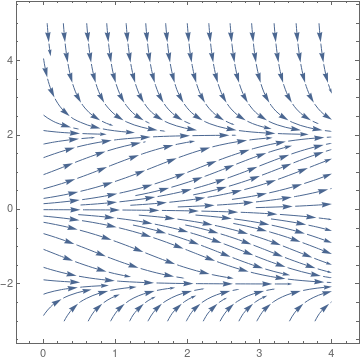
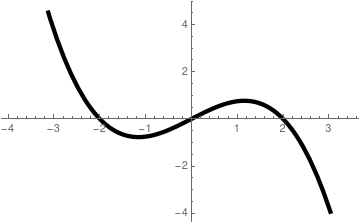
\[ \frac{{\text d}P}{{\text d}t} = r\,P(t) \left( 1 - \frac{P^2 (t)}{K} \right) , \]
and then plot the direction field
   Phase portrait for the modified logistic equation       Graph of slope function rP(1 - P²/K)

 

we see that qualitatively the solutions behave in the same manner as in the logistic equation, at least in the first quadrant. Of course, there are three equilibrium solutions, but negative critical point P = -K does not matter for population model. Another model \( \dot{P} = r\,P \left( 1 - P^3 /K \right) \) has similar properties.

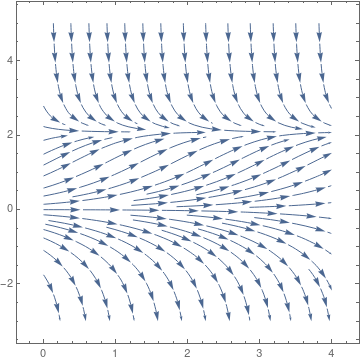
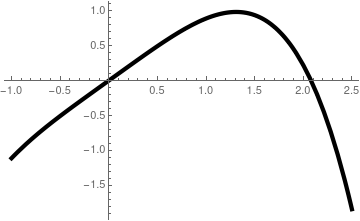
   Phase portrait for the modified logistic equation       Graph of slope function rP(1 - P³/K)

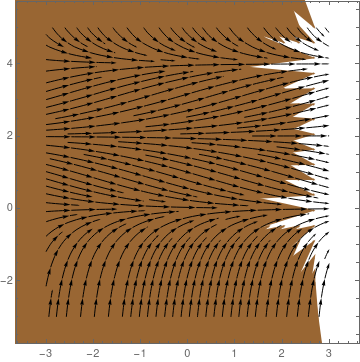
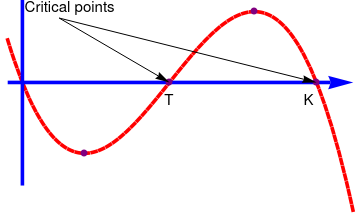
Example: The classical logistic threshold model may need to be modified so that unbounded growth does not occur when the population exceeds the threshold T. The simplest way to do this is to introduce another factor that will have the effect of making the velocity negative when the size of population becomes very large. Hence, we consider the model

\[ \dot{P} = -r \,P \left( 1 - \frac{P}{K} \right) \left( 1 - \frac{P}{T} \right) , \]
where r > 0 and 0 < T < K. Upon plotting its direction field and slope function, we can analyze the critical points of this model.
StreamPlot[{1, -y*(1 - y/2)*(1 - y/4)}, {x, -3, 3}, {y, -3, 5}, PerformanceGoal -> "Quality", StreamPoints -> Fine, StreamStyle -> Black, VectorPoints -> 20, VectorStyle -> {Arrowheads[4], Brown}]
Then we plot the slope function:
slope = Plot[-P*(1 - P/2)*(1 - P/4), {P, -0.2, 4.5}, PlotStyle -> {Thickness[0.01], Dashed, Red}, Axes -> False, Epilog -> {{Arrow[{{0.5, 0.35}, {2.0, 0}}], Arrow[{{0.5, 0.35}, {4.0, 0}}], Text[Style["Critical points", FontSize -> 14, Black], {0.65, 0.41}]}, Text[Style["T", FontSize -> 14, Black], {2.0, -0.1}], Text[Style["K", FontSize -> 14, Black], {3.9, -0.1}]}] axes1 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{-0.2, 0}, {4.5, 0}}]}] axes2 = Graphics[{Blue, Thickness[0.01], Arrowheads[0.07], Arrow[{{0, -0.56}, {0, 0.9}}]}]
p2 = Graphics[{PointSize[Large], Purple, Point[{3.1547005383787914, 0.38490017945975047}]}]
FindMinimum[-P*(1 - P/2)*(1 - P/4), {P, 1}]
pk = Graphics[{PointSize[Large], Purple, Point[{4, 0}]}]
pt = Graphics[{PointSize[Large], Purple, Point[{2, 0}]}]
p1 = Graphics[{PointSize[Large], Purple, Point[{0.8452994615144672, -0.3849001794597504}]}]
Show[slope, axes1, axes2, p1, p2, pk, pt]
   Phase portrait for the threshold logistic equation       Graph of slope function -rP(1 - P/K)(1 - P/T)
   ■

 

Andrewartha and Birch (1954) pointed out the ecological importance of spatial structure to the maintenance of populations based on studies of insect populations. They observed that although local patches become frequently extinct, migrants from other patches subsequently recolonize extinct patches, thus allowing the population to persist globally.

Levins in 2015.

In 1969, Richard Levins introduced the concept of metapopulations. This was a very influential paper that is highly cited even today. Richard Levins was of Ukrainian Jewish heritage and was born in Brooklyn, New York. Richard "Dick" Levins (1930--2016) was an extropical farmer turned ecologist, a population geneticist, biomathematician, mathematical ecologist, and philosopher of science who had researched diversity in human populations. Until his death, Levins was a university professor at the Harvard T.H. Chan School of Public Health and a long-time political activist. He was best known for his work on evolution and complexity in changing environments and on metapopulations. A metapopulation is a collection of subpopulations. Each subpopulation occupies a patch, and different patches are linked via migration of individuals between patches. Subpopulations may go extinct, thus leaving a patch vacant. Vacant patches may be recolonized by migrants from other subpopulations. This was a major theoretical advance: The metapopulation concept provided a theoretical framework for studying spatially structured populations, such as those studied by Andrewartha and Birch.

Levins' writing and speaking is extremely condensed. He was known throughout his lengthy career for his ability to make connections between seemingly disparate topics such as biology and political theory. This, combined with his Marxism, has made his analyses less well-known than those of some other ecologists and evolutionists who were adept at popularization. His research had the goal of making the obscure obvious by finding ways to visualize complex phenomena. Recent work examined the variability of health outcomes as an indicator of vulnerability to multiple non-specific stresses in human communities. One story of his Chicago years is that, in order to understand his lectures, his graduate students each needed to attend Levins' courses three times: the first time to acclimate themselves to the speed of his delivery and the difficulty of his mathematics; the second to get the basic ideas down; and the third to pick up his subtleties and profundities.

In Levins model, we keep track of the fraction of patches that is occupied by subpopulations. Subpopulations go extinct at a constant rate and we can set the time scale so that the rate is equal to 1. Vacant patches can be colonized at a rate that is proportional to the fraction of occupied patches; the constant of proportionality is denoted by k. If we call p(t) the proportion of occupied patches at time t, then writing \( p= p(t) , \) we find

\[ \frac{{\text d}p}{{\text d}t} = k\,p \left( 1- p \right) - p . \]

The first term on the right-hand side describes the colonization process. Note that an increase in the fraction of occupied patches occurs only if a vacant patch becomes occupied (the term 1 - p). The minus sign in front of the second term shows that an extinction event decreases the fraction of occupied patches.

To find equilibria, we set \( f(p) = k\,p \left( 1-p \right) -p \) and solve the equation f(p) = 0 for p:

\[ k\,p \left( 1- p \right) - p =0 . \]
Factoring p yields
\[ p \left[ k \left( 1- p \right) - 1 \right] =0 . \]
We find as one solution \( p^{\ast} = 0 . \) The other solution satisfies
\[ k \left( 1- p \right) - 1 =0 \qquad \Longrightarrow \qquad p= 1- \frac{1}{k} . \]
That is, the second solution is \( p^{\ast} = 1- 1/k . \) To make biological sense, we require the solution to be between 0 and 1. Since k > 0, we see that p* < 1. To make sure that p* > 0, we need k > 1. Since the derivative \( f' (p) = k\left( 1-2p \right) -1 \) at critical points is
\[ f' (0) = k-1 > 0 \qquad \mbox{and} \qquad f' (1-1/k) = 1-k < 0 \quad\mbox{for }\ k > 1, \]
we conclude that p* = 0 is unstable and p* = 1 - 1/k is asymptotically stable.

We see that when 0 < k < 1, there is only one biologically relevant equilibrium, namely the trivial equilibrium p* = 0, which is locally stable. When k > 1, the trivial equilibrium becomes unstable, and a second equilibrium appears, \( p^{\ast} = 1- 1/k , \) which is locally stable.

g[x_] = Piecewise[{{0, 0 < x < 1}, {Sqrt[x - 1], 1 < x}}]
a = Plot[g[x], {x, 0, 2}, PlotStyle -> {Thick, Black}]
b = Plot[0, {x, 1, 2}, PlotStyle -> {Dashed, Thick, Blue}]
Show[a, b]
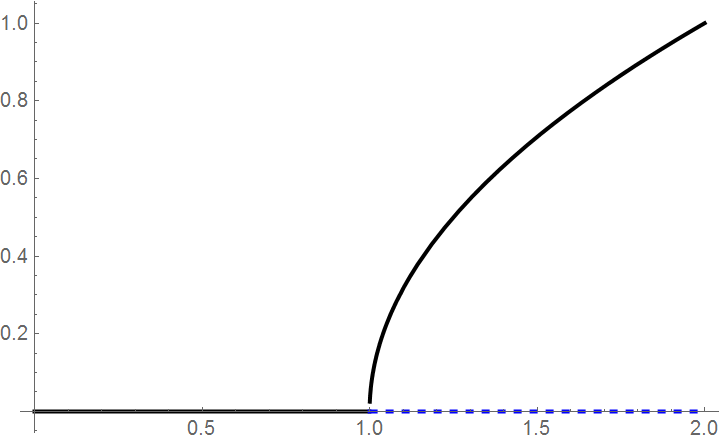
The solid lines indicate locally stable equilibria; the dashed line the unstable equilibrium.

If we graph the equilibria as a function of the parameter k, we see that there is a qualitative change in behavior at k = 1. We call this a critical value k* =1 because for k < 1, the behavior is qualitatively different from the behavior when k > 1: the stability of the trivial equilibrium changes at k* =1 and a new and nontrivial equilibrium emerges. We will discuss this phenomenon in bifurcation section.

 

 

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform) )
Return to the Part 7 (Boundary Value Problems)