Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part I of the course APMA0330
Glossary
Plotting functions
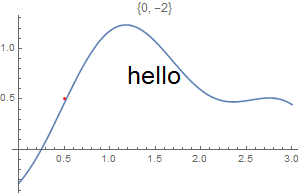
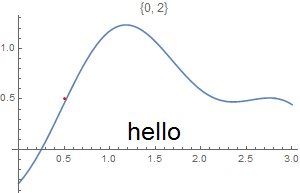
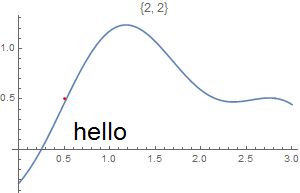
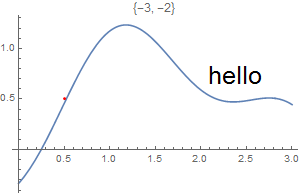
This chapter demonstrates Mathematica capability to generate graphs. We start with its basic command Plot and expose its ability to add text into figures. To place a text inside a figure, Mathematica has a special command Text[expr, coordinates, offset] that specifies an offset for the block of text relative to the coordinate given. Providing an offset { dx, dy } specifies that the point ( x, y ) should lie at relative coordinates { dx, dy } within the bounding rectangle that encloses the text. We demonstrate it with the following codes:
Epilog -> {Text[Style["hello", 25], Scaled[{0.5, 0.5}], #], Red, Point@{.5, .5}},
PlotLabel -> ToString@#] & /@ {{-2.5, 0}, {2.5, 0}, {0, -2}, {0, 2}, {2, 2}, {-3, -2}}
 |
 |
 |
 |
 |
 |
Epilog -> {Text[Style["hello", 25], Scaled[{0.5, 0.5}], #], Red, Point@{.5, .5}},
PlotLabel -> ToString@#] & /@ {{-2.5, 0}, {2.5, 0}, {0, -2}, {0, 2}, {2, 2}, {-3, -2}}
 |
 |
 |
 |
 |
 |
http://reference.wolfram.com/language/howto/AddTextToAGraphic.html.en
To add test outside the picture, see
http://reference.wolfram.com/language/howto/AddTextOutsideThePlotArea.html.en
The general reference is
http://reference.wolfram.com/language/howto/AddTextToAGraphic.html
There are someother options.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A graphic of a function can be made discrete:
Point[Table[{x, Sin[x] - 1/3 Cos[3 x]}, {x, 0, 6, .2}]]}, Axes -> True]
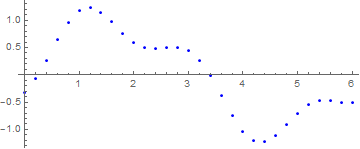
g1[0]
Show[bp, AxesOrigin -> {0, -1/3}, AxesLabel -> {"x", "y"}]
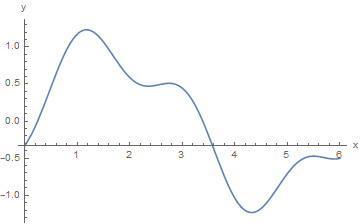
When you need to restrict the vertical range, use PlotRange command as the following example shows.
AxesLabel -> {x, (x - 1)*(x - 2)*(x - 3)*Exp[x]}]
PlotStyle -> {Black, Thick}, AxesLabel -> {x, (x - 1)*(x - 2)*(x - 3)*Exp[x]}]
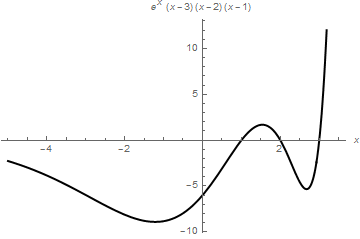 |
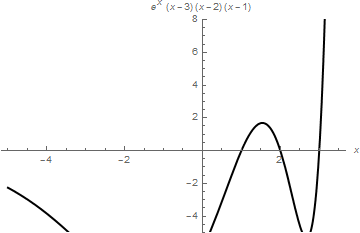 |
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)