Preface
A Riccati differential equation is an equation of the form \( y' + a(x)\,y = g(x)\,y^{\nu} +f(x), \quad \nu \ne 0,1 . \) Riccati equations have no singular solutions.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part II of the course APMA0330
Glossary
Riccati Equations
Jacopo Francesco Riccati (1676--1754) was an Venetian mathematician and jurist from Venice. He is best known for having studied the differential equation which bears his name:
\begin{equation}
y' + p(x)\,y = g(x)\,y^2 + h(x) , \label{EqRiccati.1}
\end{equation}
where p, g, and h are some real-valued given functions. Riccati himself was concerned
with solutions to so called special Riccati equation
\begin{equation}
y' = a\,y^2 + x^{\alpha} . \label{EqRiccati.2}
\end{equation}
Riccati was educated first at the Jesuit school for the nobility in Brescia, and in 1693 he entered the
University of Padua to study law. He received a doctorate in law in 1696. Encouraged by Stefano degli
Angeli to pursue mathematics, he studied mathematical analysis. Riccati received various academic offers,
but declined them in order to devote his full attention to the study of mathematical analysis on his own.
Peter the Great invited him to Russia as president of the St. Petersburg Academy of Sciences. He was also
invited to Vienna as an imperial councilor and was offered a professorship at the University of Padua.
He declined all these offers. He was often consulted by the Senate of Venice on the construction of canals and dikes along rivers.
When h(x) = 0, we get a Bernoulli equation. The Riccati equation has much in common with linear equations; for example, it has no singular solution. Except special cases, the Riccati equation cannot be solved analytically using elementary functions or quadratures, and the most common way to obtain its solution is to represent it in series. Moreover, the Riccati equation can be reduced to the second order linear differential equation by substitution
\begin{equation}
y(x) = - \frac{u'}{g(x)\,u(x)} . \label{EqRiccati.3}
\end{equation}
Substitution of the above expression into the Riccati equation yields the second order linear differential equation for u(x):
\begin{equation*}
u'' + a(x)\, u' (x) + b(x)\, u =0, \qquad \mbox{where} \quad a(x) = p(x) - \frac{g' (x)}{g(x)} , \quad b(x) = g(x)\,h(x) . %\label{Eq.riccati.4}
\end{equation*}
Conversely, every linear homogeneous differential equation with variable coefficients \( u'' + a\,u' + b\,u = 0 \) can be reduced to the Riccati equation
\[
y' + y^2 + a(x)\,y + b(x) =0
\]
by the substitution
\[
u(x) = \exp \left\{ y(x)\,{\text d} x \right\} .
\]
It is sometimes possible to find a solution of a Riccati equation by guessing. Without knowing a solution to the Riccati equation, there is no chance of finding its general solution explicitly. If one solution ϕ is known, then substitution w = y - ϕ reduces the Riccati equation to a Bernoulli equation. Another substitution y = ϕ + 1/v also reduces the Riccati equation to a Bernoulli type.
Theorem (Liouville, 1841). The special Riccati equation
\( y' = a\,y^2 + b\, x^{\alpha} \) can be integrated in closed form via elementary functions if and only if
\[
\frac{\alpha}{2\alpha +4} \qquad\mbox{is an integer}. \qquad ▣
\]
The special Riccati equation \eqref{EqRiccati.2} can be represented as \( y' = -u' /(au) , \) where
\begin{equation}
u(x) = \sqrt{x}\,\begin{cases}
C_1 J_{1/2q} \left( \frac{\sqrt{ab}}{q} \, x^q \right) + C_2 Y_{1/2q} \left( \frac{\sqrt{ab}}{q} \,
x^q \right) , &
\quad \mbox{if } ab> 0, \\
C_1 I_{1/2q} \left( \frac{\sqrt{-ab}}{q} \, x^q \right) + C_2 K_{1/2q} \left( \frac{\sqrt{-ab}}{q} \,
x^q \right) , & \quad \mbox{if } ab< 0,
\end{cases} \label{EqRiccati.4}
\end{equation}
where \( q= 1+ \alpha /2 \) and J(t), Y(t) are Bessel functions, ,
while I(t), K(t) are modified Bessel functions. Note that the general solution depends on the
ratio \( C_1 / C_2 \) of two arbitrary constants. Actually, Mathematica knows the solution:
DSolve[{y'[x] == x^2 + (y[x])^2, y[0] == a}, y[x], x]
{{y[x] -> (-a x^2 BesselJ[-(3/4), x^2/2] Gamma[1/4] +
x^2 BesselJ[-(5/4), x^2/2] Gamma[3/4] +
BesselJ[-(1/4), x^2/2] Gamma[3/4] -
x^2 BesselJ[3/4, x^2/2] Gamma[3/
4])/(x (a BesselJ[1/4, x^2/2] Gamma[1/4] -
2 BesselJ[-(1/4), x^2/2] Gamma[3/4]))}}
\begin{equation} \label{EqRiccati.5}
y(x) = x\,\frac{-a\, J_{-3/4} \left( x^2 /2 \right) \Gamma \left( \frac{1}{4} \right) + J_{-5/4} \left( x^2 /2 \right) \Gamma \left( \frac{3}{4} \right) - J_{3/4} \left( x^2 /2 \right) \Gamma \left( \frac{3}{4} \right)}{a\, J_{1/4} \left( x^2 /2 \right) \Gamma \left( \frac{1}{4} \right) - 2\,J_{-1/4} \left( x^2 /2 \right) \Gamma \left( \frac{3}{4} \right)} .
\end{equation}
In particular, solution to the initial value problem
\( y' = x^2 + y^2 , \quad y(0) = 0 \) is
\begin{equation} \label{EqRiccati.6}
y(x) = x\,\frac{-Y_{-3/4} \left( \frac{x^2}{2} \right) + J_{-3/4} \left( \frac{x^2}{2} \right)}{Y_{1/4} \left( \frac{x^2}{2} \right) - J_{1/4} \left( \frac{x^2}{2} \right)} = x\,\frac{J_{3/4} \left( \frac{x^2}{2} \right)}{J_{-1/4} \left( \frac{x^2}{2} \right)} .
\end{equation}
We make transformation y = ur vs, which we substitute into the special Riccati equation:
\[
r\,u^{r-1} u' \,v^s + s\,u^r v^{s-1} v' = a\,u^{2r} v^{2s} + b\, x^2 .
\]
Choosing
\[
\begin{split}
r\,u^{r-1} u' \,v^s &= b\,x^2 , \\
s\,u^r v^{s-1} v' &= a\,u^{2r} v^{2s} \qquad \Longleftrightarrow \qquad s\,v' = a\, u^r v^{s+1} .
\end{split}
\]
Differentiation of the latter, we obtain
\[
s\, v'' = ar\, u^{r-1} u' \, v^{s+1} + a \left( s+1 \right) u^r v^s v' .
\]
The nonlinearity can now be removed by choosing s = -1. Then using the latter, we get
\[
s\, v'' = ab\, u^{r-1} u' \, v^{s+1} = ab\, x^2 v \qquad\mbox{or} \qquad v'' = -ab\, x^2 v .
\]
Since the equation \( v'' + ab\, x^2 v = 0 \) has the general solution expressed through Bessel functions (see section)
\[
v(x) = \sqrt{x} \left[ C_1 J_{1/4} \left( \frac{\sqrt{ab}\,x^2}{2} \right) + C_2 Y_{1/4} \left( \frac{\sqrt{ab}\,x^2}{2} \right) \right] ,
\]
where C1 and C2 are arbitrary constants, we arrive at the required formula. Using Mathematica
v[x_] = Sqrt[
x]*(k*BesselJ[1/4, alpha*x^2 /2] + BesselY[1/4, alpha*x^2 /2])
y[x_] = Simplify[v'[x]/v[x]]
Assuming[alpha > 0 && x > 0, Series[%, {x, 0, 0}]]
Normal[%]
Simplify[%]
we obtain the general solution of the
special Riccati equation:
y[x_] = Simplify[v'[x]/v[x]]
Assuming[alpha > 0 && x > 0, Series[%, {x, 0, 0}]]
Normal[%]
Simplify[%]
\[
y(x) = \frac{1}{2x} \,\frac{\sqrt{ab}\,k x^2 J_{3/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) + k\, J_{1/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) - \sqrt{ab} \, k x^2 J_{5/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) + \sqrt{ab}\, x^2 Y_{-3/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) + Y_{1/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) - \sqrt{ab} \,x^2 Y_{5/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) }{k\, J_{1/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right) + Y_{1/4} \left( \frac{\sqrt{ab}\, x^2}{2} \right)} ,
\]
where k is an arbitrary constant, and ab is positive.
▣ We can find the limit of the solution to the special Riccati equation when x → 0:
\begin{align}
\lim_{x\to 0} y(x) &= \frac{\sqrt{ab}}{8\,\Gamma^2 \left( \frac{1}{4} \right) \Gamma \left( \frac{5}{4} \right)} \left[ \sqrt{2}\, \Gamma \left( \frac{1}{4} \right) \left( \Gamma \left( -\frac{1}{4} \right) - 4\,\Gamma \left( \frac{3}{4} \right) \right) \Gamma \left( \frac{5}{4} \right) -2k\pi \left( \Gamma \left( \frac{1}{4} \right) + 4\, \Gamma \left( \frac{5}{4} \right)\right) \right] \notag
\\
&= -\frac{\sqrt{ab}}{\pi} \,\Gamma^2 \left( \frac{3}{4} \right) \left( 1+ k\right) \approx -0.477989 \left( 1 + k \right) \sqrt{ab} . \label{Eq.riccati.6}
\end{align}
Example 1: The standard Riccati equation
\[
y' = x^2 + y^2
\tag{1.2}
\]
has the general solution \( y= -u' /u , \) given
\[
u(x) = \sqrt{x} \left[ C_1 J_{1/4} \left( x^2 /2 \right) + C_2 Y_{1/4} \left( x^2 /2 \right) \right] ,
\]
where C1 and C2 are arbitrary constants.
The solution of the Riccati equation subject to the homogeneous initial condition y(0) = 0 is known from Eq.\eqref{EqRiccati.6}:
\begin{equation*}
y(x) = x\,\frac{-Y_{-3/4} \left( \frac{x^2}{2} \right) + J_{-3/4} \left( \frac{x^2}{2} \right)}{Y_{1/4} \left( \frac{x^2}{2} \right) - J_{1/4} \left( \frac{x^2}{2} \right)} . %\label{Eq.riccati.7}
\end{equation*}
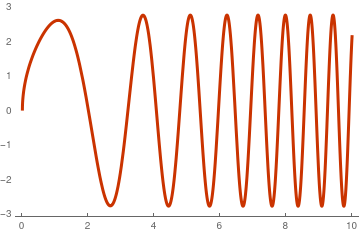
This solution blows up at x ≈ 2.00315 where the denominator is zero.
sol = DSolveValue[{y'[x] == x^2 + (y[x])^2, y[0] == a}, y[x], x];
FindRoot[Denominator[sol /. a -> 0] == 0, {x, 2}]
FindRoot[Denominator[sol /. a -> 0] == 0, {x, 2}]
2.003147359426885
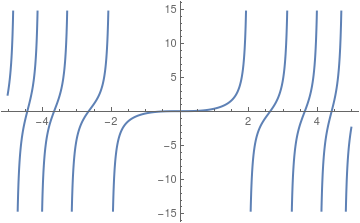
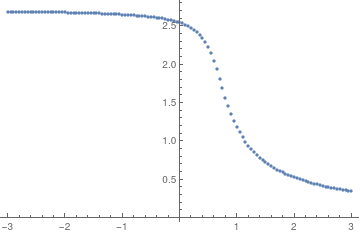
The denominator in formula \eqref{EqRiccati.6} has infinite (countable) many roots, which is seen from its plot
Plot[Evaluate[Denominator[sol /. a -> 0]], {x, 0, 10},
PlotTheme -> "Web"]
|
soln = DSolve[{y'[x] == y[x]^2 + x^2, y[0] == C}, y[x], x]
hold = Part[soln, 1, 1, 2] dansoln = FullSimplify[ hold /. {C -> 0} ] danseries = FullSimplify[Series[dansoln, {x, 0, 15}]] dansoln /. {x-> 0.5} Plot[dansoln, {x,-5,5}, PlotStyle->{Thick, Blue}]
0.0417911
|
|
x0 = Last[
Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == 0}, y, {x, 0, 3},
EvaluationMonitor :> Sow[x]]][[2, 1]]] // Quiet
2.0031471284132385
which is accurate up to 7 decimal places.
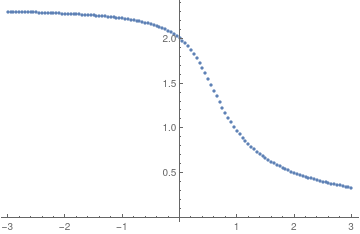
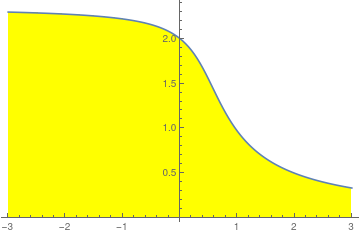
Next, we plot singular points for the family of singular solutions of the initial value problems
\[
y' = x^2 + y^2 , \qquad y(0) = a .
\]
A singular point x0 where solution blows up is plotted together with the corresponding initial condition giving a set of points on the plane: (x0, 𝑎).
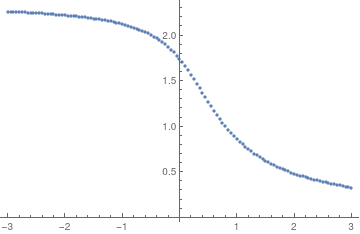
data = {#,
Quiet[Last[
Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == #},
y, {x, 0, 10}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]} & /@
Range[-3, 3, 0.05]
ListPlot[data] ListPlot[{#, Quiet[Last[ Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == #}, y, {x, 0, 10}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]} & /@ Range[-3, 3, 0.05]]
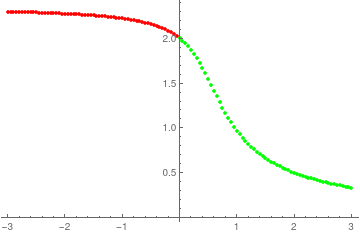
If # is in the 2nd place in the list {...}, the order of the list is changed.
ListPlot[data] ListPlot[{#, Quiet[Last[ Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == #}, y, {x, 0, 10}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]} & /@ Range[-3, 3, 0.05]]
{Quiet[Last[
Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == #}, y, {x, 0, 10},
EvaluationMonitor :> Sow[x]]][[2, 1]]]], #} & /@
Range[-3, 3, 0.05]
ListPlot[{#} & /@ data, PlotStyle -> (If[#[[1]] < 0, Red, Green] & /@ data)]
ListPlot[{#} & /@ data, PlotStyle -> (If[#[[1]] < 0, Red, Green] & /@ data)]
|
|
||
| Solution diagram. | Solution diagram with extra #. |
ListLinePlot[{#,
Quiet[Last[
Reap[NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == #},
y, {x, 0, 10}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]} & /@
Range[-3, 3, 0.05], Filling -> Axis, FillingStyle -> Yellow]
The initial value problem \( y' = y^2 + x^2 , \quad y(0) =0 \) has two forms of solutions \eqref{EqRiccati.6} expressed through Bessel functions of the first kind only:
\begin{equation*}
y(x) = x\,\frac{J_{3/4} \left( \frac{x^2}{2} \right)}{J_{-1/4} \left( \frac{x^2}{2} \right)} = x\,\frac{-Y_{-3/4} \left( \frac{x^2}{2} \right) + J_{-3/4} \left( \frac{x^2}{2} \right)}{Y_{1/4} \left( \frac{x^2}{2} \right) - J_{1/4} \left( \frac{x^2}{2} \right)}.
\end{equation*}
To convince you that this is the same solution presented in another form, we do two things. First, we expand the above solution into Maclarin series and compare it with true expansion. Second, we verify that our function satisfies the given Riccati equation and the initial condition because the solution of such initial value problem is unique.
AsymptoticDSolveValue[{y'[x] == x^2 + (y[x])^2, y[0] == 0},
y[x], {x, 0, 16}]
\[
y(x) = \frac{1}{3}\, x^3 + \frac{1}{63}\, x^7 + \frac{2}{2079}\, x^{11} + \frac{13}{218295}\,x^{15} + O\left( x^{16} \right)
\]
First, we define two solution-functions in Mathematica:
f[x_] = x*BesselJ[3/4, x^2 /2]/BesselJ[-1/4, x^2 /2];
g[x_] = x*(BesselJ[-3/4, x^2 /2] - BesselY[-3/4, x^2 /2])/(BesselY[1/4, x^2 /2] - BesselJ[1/4, x^2 /2]);
We check their power series:
g[x_] = x*(BesselJ[-3/4, x^2 /2] - BesselY[-3/4, x^2 /2])/(BesselY[1/4, x^2 /2] - BesselJ[1/4, x^2 /2]);
N[Series[f[x], {x, 0, 16}]]
N[Series[g[x], {x, 0, 16}]]
Then we check whether these two functions are solutions of the Riccati equation (1.2):
N[Series[g[x], {x, 0, 16}]]
FullSimplify[D[f[x], x] - x^2 - (f[x])^2]
FullSimplify[D[g[x], x] - x^2 - (g[x])^2]
Finally, we check the initial conditions
FullSimplify[D[g[x], x] - x^2 - (g[x])^2]
f[0]
Limit[g[x], x -> 0]
Limit[g[x], x -> 0]
In order to determine where the solution blows up, we find the zero of the denominator:
FindRoot[BesselY[1/4, x^2 /2] - BesselJ[1/4, x^2 /2], {x, 2.0}]
{x -> 2.003147359426885}
FindRoot[BesselJ[-1/4, x^2 /2], {x, 2.0}]
{x -> 2.003147359426885}
Then we evaluate some numerical values:
f[x_] = x*BesselJ[3/4, x^2 /2]/BesselJ[-1/4, x^2 /2];
g[x_] = x*(BesselJ[-3/4, x^2 /2] - BesselY[-3/4, x^2 /2])/(BesselY[1/4, x^2 /2] - BesselJ[1/4, x^2 /2]);
N[f[0.75]-g[0.75]]
g[x_] = x*(BesselJ[-3/4, x^2 /2] - BesselY[-3/4, x^2 /2])/(BesselY[1/4, x^2 /2] - BesselJ[1/4, x^2 /2]);
N[f[0.75]-g[0.75]]
-2.77556*10^-17
which is numerically zero.
The solution of the Riccati equation \( y' = y^2 + x^2 \) subject to the initial condition y(0) = 1 is
\[
y(x) = x\,\frac{\left( \pi - \Gamma^2 \left( \frac{3}{4} \right) \right) J_{-3/4} \left( \frac{x^2}{2} \right) - \Gamma^2 \left( \frac{3}{4} \right) Y_{-3/4} \left( \frac{x^2}{2} \right)}{\left( \pi - \Gamma^2 \left( \frac{3}{4} \right) \right) J_{1/4} \left( \frac{x^2}{2} \right) + \Gamma^2 \left( \frac{3}{4} \right) Y_{1/4} \left( \frac{x^2}{2} \right)} .
\tag{1.2}
\]
This solution blows up at x ≈ 0.969811 where the denominator is zero.
DSolve[{u'[x] == x^2 + (u[x])^2 , u[0] == 1}, u, x]
FindRoot[BesselJ[1/4, x^2/2] Gamma[1/4] - 2 BesselJ[-(1/4), x^2/2] Gamma[3/4] == 0, {x, 1}]
FindRoot[BesselJ[1/4, x^2/2] Gamma[1/4] - 2 BesselJ[-(1/4), x^2/2] Gamma[3/4] == 0, {x, 1}]
{x -> 0.969811}
The solution of the initial value problem
\[
y' = x^2 + y^2 , \qquad y(0) = -1 ,
\]
is
\[
y(x) = x\,\frac{\left( \pi + \Gamma^2 \left( \frac{3}{4} \right) \right) J_{-3/4} \left( \frac{x^2}{2} \right) - \Gamma^2 \left( \frac{3}{4} \right) Y_{-3/4} \left( \frac{x^2}{2} \right)}{\left( \pi + \Gamma^2 \left( \frac{3}{4} \right) \right) J_{1/4} \left( \frac{x^2}{2} \right) + \Gamma^2 \left( \frac{3}{4} \right) Y_{1/4} \left( \frac{x^2}{2} \right)} .
\tag{1.3}
\]
This solution blows up at x ≈ 4.1785 where the denominator is zero.
DSolve[{u'[x] == x^2 + (u[x])^2 , u[0] == -1}, u, x]
FindRoot[ BesselJ[1/4, x^2/2] Gamma[1/4] + 2 BesselJ[-(1/4), x^2/2] Gamma[3/4] == 0, {x, 4}]
FindRoot[ BesselJ[1/4, x^2/2] Gamma[1/4] + 2 BesselJ[-(1/4), x^2/2] Gamma[3/4] == 0, {x, 4}]
{x -> 4.17851}
■ Example 2: We consider a problem similar to the previous example that involves another standard Riccati equation
\[
y' = x^2 - y^2 .
\tag{2.1}
\]
Its solution
is expressed as \( y= u' /u , \) where
\[
u(x) = \sqrt{x} \left[ C_1 I_{1/4} \left( x^2 /2 \right) + C_2 K_{1/4} \left( x^2 /2 \right) \right] ,
\]
When we impose the homogeneous conditions y(0) = 0, then its solution becomes
\[
y(x) = x\,\frac{I_{-3/4} \left( \frac{x^2}{2} \right) \pi \sqrt{2} - 2\,K_{3/4} \left( \frac{x^2}{2} \right)}{\pi \sqrt{2}\,I_{1/4} \left( \frac{x^2}{2} \right) + 2\, K_{1/4} \left( \frac{x^2}{2} \right)} .
\tag{2.2}
\]
The initial value problem
\[
y' = x^2 - y^2 , \qquad y(0) =1 ,
\tag{2.3}
\]
has the solution
\[
y(x) = x\,\frac{\left( \pi + \Gamma^2 \left( \frac{3}{4} \right) \sqrt{2} \right) I_{-3/4} \left( \frac{x^2}{2} \right) \pi - 2\, \Gamma^2 \left( \frac{3}{4} \right) K_{3/4} \left( \frac{x^2}{2} \right)}{\left( \pi + \Gamma^2 \left( \frac{3}{4} \right) \sqrt{2} \right) I_{1/4} \left( \frac{x^2}{2} \right) \pi + 2\,\Gamma^2 \left( \frac{3}{4} \right) K_{1/4} \left( \frac{x^2}{2} \right)} .
\tag{2.4}
\]
|
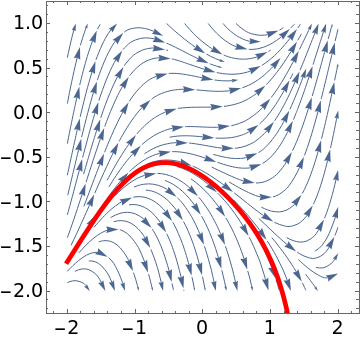
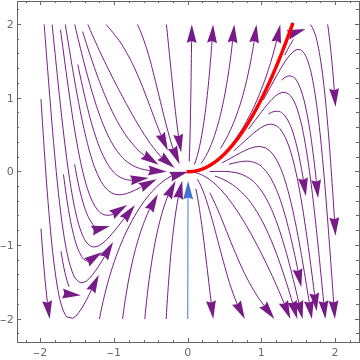
We plot the separatrix (in red) for the Riccati equation
\( y' = x^2 - y^2 \) that separates solutions approaching +∞ from solutions that go to -∞.
sp = StreamPlot[{1, x^2 - y^2}, {x, -2, 2}, {y, -2, 1},
StreamScale -> Medium, LabelStyle -> {FontSize -> 18, Black}];
curve = NDSolve[{y'[x] == x^2 - (y[x])^2, y[0] == -0.7134}, y, {x, -2, 2}]; cp = Plot[Evaluate[y[x] /. curve], {x, -2, 2}, PlotStyle -> {Thickness[0.015], Red}]; Show[sp, cp] |
|
| Separatrix for the Riccati equation (2.1). | Mathematica code |
If we consider a similar Riccati equation
\[
y' = y^2 - x^2
\tag{2.5}
\]
its direction field is very similar. Th4e solution of Eq.(2.5) subject to the homogeneous initial condition is
\[
y = x\, \frac{I_{-3/4} \left( \frac{x^2}{2} \right) \pi\sqrt{2} - 2\, K_{3/4} \left( \frac{x^2}{2} \right)}{\pi\sqrt{2}\,I_{1/4} \left( \frac{x^2}{2} \right) + 2\, K_{1/4} \left( \frac{x^2}{2} \right)} , \qquad y(0) = 0.
\tag{2.6}
\]
However, for another initial condition, its solution becomes
\[
y = x\, \frac{I_{-3/4} \left( \frac{x^2}{2} \right) \pi \left( \sqrt{2}\,\Gamma^2 \left( \frac{3}{4} \right) + \pi \right) - 2\, K_{3/4} \left( \frac{x^2}{2} \right) \Gamma \left( \frac{3}{4} \right)}{\pi \left( \sqrt{2}\,\Gamma^2 \left( \frac{3}{4} \right) + \pi \right) I_{1/4} \left( \frac{x^2}{2} \right) + 2\, K_{1/4} \left( \frac{x^2}{2} \right) \Gamma \left( \frac{3}{4} \right)} , \qquad y(0) = 1.
\tag{2.7}
\]
|
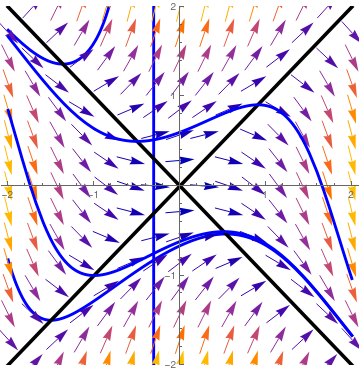
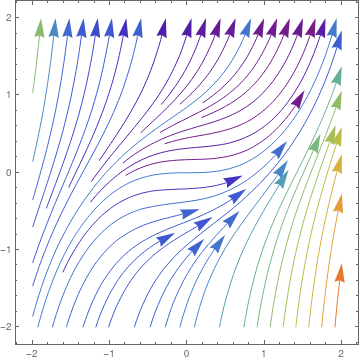
We plot two nullclines (in black) for the Riccati equation
\( y' = y^2 - x^2 \) and some typical solutions.
dfield = VectorPlot[{1, y^2 - x^2}, {x, -2, 2}, {y, -2, 2},
Axes -> True, VectorScale -> {Small, Automatic, None},
AxesLabel -> {"x", "dydx=y^2 - x^2"}]
l1 = Plot[x, {x, -2, 2}, PlotStyle -> {Thickness[0.01], Black}]; l2 = Plot[-x, {x, -2, 2}, PlotStyle -> {Thickness[0.01], Black}]; sol1 = NDSolve[{y'[x] == (y[x])^2 - x^2, y[-1.5] == -1.5}, y, {x, -2, 2}] s1 = Plot[y[x] /. sol1, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol2 = NDSolve[{y'[x] == (y[x])^2 - x^2, y[-1.0] == 1.6}, y, {x, -2, 2}] s2 = Plot[y[x] /. sol2, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol3 = NDSolve[{y'[x] == (y[x])^2 - x^2, y[0] == 0.6}, y, {x, -2, 2}] s3 = Plot[y[x] /. sol3, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol4 = NDSolve[{y'[x] == (y[x])^2 - x^2, y[-1.0] == -1.0}, y, {x, -2, 2}] s4 = Plot[y[x] /. sol4, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] Show[s1, s2, l1, l2, dfield, s3, s4, AspectRatio -> 1] |
|
| Two nullclines for the Riccati equation (2.5). | Mathematica code |
■
Example 3: : Consider the Riccati equation
\[
y' = y^2 -x .
\tag{3.1}
\]
|
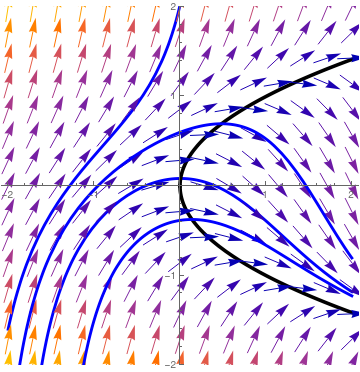
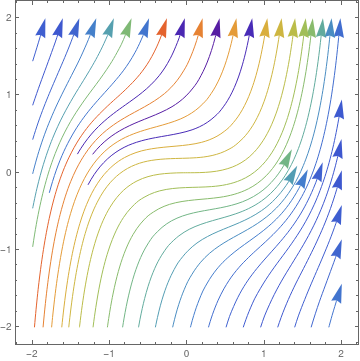
We plot the nullcline (in black) y² = x and phase portrait) for the Riccati equation
\( y' = y^2 - x. \)
dfield = VectorPlot[{1, y^2 - x}, {x, -2, 2}, {y, -2, 2},
Axes -> True, VectorScale -> {Small, Automatic, None},
AxesLabel -> {"x", "dydx=y^2 - x^2"}];
l1 = Plot[Sqrt[x], {x, -2, 2}, PlotStyle -> {Thickness[0.01], Black}]; l2 = Plot[-Sqrt[x], {x, -2, 2}, PlotStyle -> {Thickness[0.01], Black}]; sol1 = NDSolve[{y'[x] == (y[x])^2 - x, y[-1.5] == -1.5}, y, {x, -2, 2}]; s1 = Plot[y[x] /. sol1, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol2 = NDSolve[{y'[x] == (y[x])^2 - x, y[-2.0] == -1.6}, y, {x, -2, 2}]; s2 = Plot[y[x] /. sol2, {x, -2, 1.5}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol3 = NDSolve[{y'[x] == (y[x])^2 - x, y[0] == 0.6}, y, {x, -2, 2}]; s3 = Plot[y[x] /. sol3, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] sol4 = NDSolve[{y'[x] == (y[x])^2 - x, y[-1.0] == -1.5}, y, {x, -2, 2}]; s4 = Plot[y[x] /. sol4, {x, -2, 2}, PlotStyle -> {Thickness[0.008], Blue}, PlotRange -> {-2, 2}] Show[s1, s2, l1, l2, dfield, s3, s4, AspectRatio -> 1] |
|
| The nullcline and phase portrait for the Riccati equation (3.1). | Mathematica code |
■
Example 4: : Consider the Riccati equation
\[
y' = 2y/x+y^2 -x^4 .
\tag{4.1}
\]
|
We plot the separatrix and the direction field
field = StreamPlot[{1, 2*y/x + y^2 - x^4}, {x, -2, 2}, {y, -2, 2},
StreamColorFunction -> "Rainbow", StreamPoints -> 42,
StreamScale -> {Full, All, 0.04}];
sol = NDSolve[{y'[x] == 2*y[x]/x + (y[x])^2 - x^4 , y[0.1] == 0.01}, y[x], {x, 0, 2}]; curve = Plot[Evaluate[y[x] /. sol], {x, 0, 2}, PlotRange -> {{0, 2}, {-2, 2}}, PlotStyle -> {Red, Thickness[0.01]}]; Show[field, curve] |
| Direction field and separatrix (in red). | Mathematica code. |
The given Riccati equation can be solved by substitution \( y =x^2 +1/v(x) , \) where y1 = x² is a particular solution of the given Riccati equation.
R[x_, y_] = (y'[x] - 2 y[x]/x - y[x]^2 + x^4 )
y1[x_] = x^2
R[x, y1]
Simplify[Expand[v[x]^2 R[x, Function[t, t + t/v[t]]]]]
DSolve[% == 0, v[x], x] (* solve linear equation for v *)
y2[x_] = Simplify[(y1[x] + 1/v[x]) /. %[[1]]]
y1[x_] = x^2
R[x, y1]
Simplify[Expand[v[x]^2 R[x, Function[t, t + t/v[t]]]]]
DSolve[% == 0, v[x], x] (* solve linear equation for v *)
y2[x_] = Simplify[(y1[x] + 1/v[x]) /. %[[1]]]
Out[11]= x^4 - (2 y[x])/x - y[x]^2 + Derivative[1][y][x]
Out[12]= x^2
Out[13]= 0
Out[14]= -(1 + 2 x^2) v[x] + (-1 - x^2 + x^4) v[x]^2 - x (x + Derivative[1][v][x])
Out[15]= {{v[x] -> -(x (-(E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x))/(2 x)) + (
E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x))/(2 x^2) - (
E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x) ((5 x^2)/3 - 1/3 x (3 + 2 x)))/(
2 x) + (-((E^(-(1/6) x^2 (3 + 2 x)) (-1 + x))/x^2) +
E^(-(1/6) x^2 (3 + 2 x))/x + ( E^(-(1/6) x^2 (3 + 2 x)) (-1 + x) (-(x^2/3) -
1/3 x (3 + 2 x)))/x) C[1]))/((-1 - x^2 + x^4) (-((E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x))/(
2 x)) + (E^(-(1/6) x^2 (3 + 2 x)) (-1 + x) C[1])/x))}}
Out[16]= (E^((2 x^3)/3) (-1 - x + x^2) + 2 (-1 + x + x^2) C[1])/(E^((
2 x^3)/3) + 2 C[1])
■ Out[12]= x^2
Out[13]= 0
Out[14]= -(1 + 2 x^2) v[x] + (-1 - x^2 + x^4) v[x]^2 - x (x + Derivative[1][v][x])
Out[15]= {{v[x] -> -(x (-(E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x))/(2 x)) + (
E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x))/(2 x^2) - (
E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x) ((5 x^2)/3 - 1/3 x (3 + 2 x)))/(
2 x) + (-((E^(-(1/6) x^2 (3 + 2 x)) (-1 + x))/x^2) +
E^(-(1/6) x^2 (3 + 2 x))/x + ( E^(-(1/6) x^2 (3 + 2 x)) (-1 + x) (-(x^2/3) -
1/3 x (3 + 2 x)))/x) C[1]))/((-1 - x^2 + x^4) (-((E^((2 x^3)/3 - 1/6 x^2 (3 + 2 x)) (1 + x))/(
2 x)) + (E^(-(1/6) x^2 (3 + 2 x)) (-1 + x) C[1])/x))}}
Out[16]= (E^((2 x^3)/3) (-1 - x + x^2) + 2 (-1 + x + x^2) C[1])/(E^((
2 x^3)/3) + 2 C[1])
Example 5: : We consider some modifications of the standard Riccati equation. In particular, we start with the following two:
\[
y' = x^2 +y^2 -xy
\tag{5.1}
\]
and
\[
y' = x^2 +y^2 +xy .
\tag{5.2}
\]
First, we plot phase portraits for these equations:
StreamPlot[{1, x^2 + y^2 - x*y}, {x, -2, 2}, {y, -2, 2},
StreamColorFunction -> "Rainbow", StreamPoints -> 42,
StreamScale -> {Full, All, 0.04}]
treamPlot[{1, x^2 + y^2 + x*y}, {x, -2, 2}, {y, -2, 2}, StreamColorFunction -> "Rainbow", StreamPoints -> 42, StreamScale -> {Full, All, 0.04}]
treamPlot[{1, x^2 + y^2 + x*y}, {x, -2, 2}, {y, -2, 2}, StreamColorFunction -> "Rainbow", StreamPoints -> 42, StreamScale -> {Full, All, 0.04}]
|
|
|
| Phase portrait for y' = x² + y² −xy. | Phase portrait for y' = x² + y² + xy. |
\[
y' = x^2 +y^2 pm xy , \qquad y(0) = b,
\tag{5.3}
\]
blows up.
ListPlot[{#,
Quiet[Last[
Reap[NDSolve[{y'[x] == x^2 + (y[x])^2 - x*y[x], y[0] == #},
y, {x, 0, 3}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]} & /@
Range[-3, 3, 0.05]]
For Eq.(5.2), we use table option:
values = Range[-3, 3, 0.05]
solution = Table[ {i, Quiet[ Last[Reap[ NDSolve[{y'[x] == x^2 + (y[x])^2 + x*y[x], y[0] == i}, y, {x, 0, 3}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]}, {i, values} ]
ListPlot[solution]
solution = Table[ {i, Quiet[ Last[Reap[ NDSolve[{y'[x] == x^2 + (y[x])^2 + x*y[x], y[0] == i}, y, {x, 0, 3}, EvaluationMonitor :> Sow[x]]][[2, 1]]]]}, {i, values} ]
ListPlot[solution]
|
|
|
| Existence diagram for y' = x² + y² −xy. | Existence diagram for y' = x² + y² + xy. |
- Haaheim, D.R. and Stein, F.M., Methods of Solution of the Riccati Differential Equation, Mathematics Magazine, 1969, Vol. 42, No. 5, pp. 233--240; https://doi.org/10.1080/0025570X.1969.11975969
- Robin, W., A new Riccati equation arising in the theory of classical orthogonal polynomials, International Journal of Mathematical Education in Science and Technology, 2003, Volume 34, 2003 - Issue 1, pp. 31--42. https://doi.org/10.1080/0020739021000018746
Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part II of the course APMA0330