Preface
This section discusses a simplified version of the Adomian decomposition method first concept of which was proposed by Randolf Rach in 1989 that was crystallized later in a paper published with his colleagues G. Adomian and R.E. Meyers. That is way this technique is frequently referred to as the Rach--Adomian--Meyers modified decomposition method (MDM for short). Initially, this method was applied to power series expansions, which was based on the nonlinear transformation of series by the Adomian--Rach Theorem. Similar to the Runge--Kutta methods, the MDM can be implemented in numerical integration of differential equations by one-step methods. In case of polynomials or power series, it shows the advantage in speed and accuracy of calculations when at each step the Adomian decomposition method allows one to perform explicit evaluations.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part VII of the course APMA0330
Glossary
Falkner--Skan layer
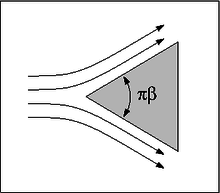
The Falkner–Skan boundary layer (named after V. M. Falkner and Sylvia W. Skan) describes the steady two-dimensional laminar boundary layer that forms on a wedge, i.e. flows in which the plate is not parallel to the flow. It is a generalization of the Blasius boundary layer. The Prandtl's boundary layer equations for steady incompressible flow with constant viscosity and density can be reduced to the Falkner–Skan equation for single function f(η)
|

|
| Wedge flow | An F/A-18 Hornet creating a vapor cone at transonic speed just before reaching the speed of sound |
Example: The problem is to find the potential V(x) that satisfies the following second order ordinary differential equation and boundary conditions
Example: The Thomas--Fermi problem for the neutral atom [17,18] writes in terms of a function u(x):
Example: Consider the equation of the flow of a third grade fluid in a porous half space which has been investigated by Hayat et al and Ahmad. The formulation of this problem in terms of f(z) is
- Falkner–Skan boundary layer
- Falkner V. M. and Skan, S. W. Advisory Committee for Aeronautics, 1930, no 1314, 1930.
- Falkner V. M. and Skan, S. W. Some approximate solutions of the boundary-layer equations. Philosophical Magazine, 1931, Vol. 12 12 , 865-896 (1931).
- Abbasbandy, S. and Dervillie, C., analytic continuation of Taylor series and the boundary value problems of some nonlinear ordinary differential equations, 2011,
- F. Ahmad, A simple analytical solution for the steady flow of a third grade fluid in a porous half space, Communications in Nonlinear Science and Numerical Simulation, 2009, Vol. 14, pp. 2848.
- Asaithambi, A. A series solution of the Falkner–Skan equation using the crocco–wang transformation, International Journal of Modern Physics, 2017, Vol. 28, No. 11, 1750139; https://doi.org/10.1142/S012918311750139X
- Fermi, E., Un Metodo Statistico per la Determinazione dialcune Priopriet`a dell’Atomo, Rendiconti Academia Dei Lincei, 1927, Vol. 6, pp. 602--607.
- T. Hayat, F. Shahzad and M. Ayub, Analytical solution for the steady flow of the third grade fluid in a porous half space, Applied Mathematical Modelling, 2007, Volume 31, Issue 11, November 2007, Pages 2424-2432; https://doi.org/10.1016/j.apm.2006.09.008
- Kazem, S., Rad, J.A., Parand, K., Abbasbandy, S., A new method for solving steady flow of a third-grade fluid in a porous half space based on radial basis functions, Verlag der Zeitschrift f ̈ur Naturforschung, Tbingen, 2011; doi: 10.5560/ZNA.2011-0014
- Polchinski, J., Renormalization and effective lagrangians, Nuclear Physics B 1984, Vol. 231 (1984) 269--295.
- L. H. Thomas, The calculation of atomic fields, Mathematical Proceedings of the Cambridge Philosophical Society, 1927, Vol 23, pp. 542--548. doi:10.1017/S0305004100011683
- H. Weyl, Concerning the Differential Equations of Some Boundary Layer Problems, Proceedings of the National Academy of Sciience of the United States of America, 1941, Vol. 27, No 12, pp. 578--583; doi: 10.1073/pnas.27.12.578
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)