Preface

This section is devoted to a special modification of the Euler numerical rule, known as the Heun method.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part III of the course APMA0330

Glossary

Heun's Methods

Karl Heun
Since the Euler rule requires a very small step size to produce sufficiently accurate results, many efforts have been devoted to the development of more efficient methods. Our next step in this direction includes Heun's method, which was named after a German mathematician Karl Heun (1859--1929), who made significant contributions to developing the Runge--Kutta methods. Actually, the algorithm named after Heun was discovered by Carl Runge.

According to the following definition, Heun's method is an explicit one-step method.

Definition: An explicit one-step method for computation of an approximation yn+1 of the solution to the initial value problem y' = f(x,y),    y(x0) = y0, on a grid of points x0 < x1 < ··· with step size h has the form
\[ y_{n+1} = y_n + h\,\Phi (x,y_n ,h), \qquad n=0,1,2,\ldots , \quad y_0 = y(x_0 ). \]
Here Φ(·, ·, ·) is called incremental function of the one-step method.

 

Trapezoid Rule

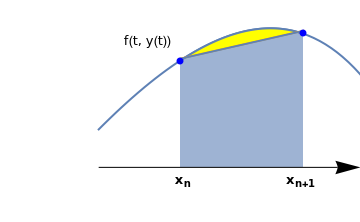
Suppose that we want to solve the initial value problem for the first order differential equation

\begin{equation} \label{EqHeun.1} y' = f(x,y), \quad y(x_0 ) = y_0\qquad \Longleftrightarrow \qquad y(x) = y(x_0 ) + \int_{x_0}^x f\left( s, y(s) \right) {\text d}s , \end{equation}
which is equivalent to the integral equation:
\begin{equation} \label{EqHeun.2} y(x_{n+1}) - y(x_n ) = \int_{x_n}^{x_{n+1}} f(t, y(t))\,{\text d} t . \end{equation}
   
curve = Plot[x - Exp[x - 0.05] + 1.5, {x, -1.0, 0.7}, PlotStyle -> Thick, Axes -> False, Epilog -> {Blue, PointSize@Large, Point[{{-0.5, 0.42}, {0.25, 0.53}}]}, PlotRange -> {{-1.6, 0.6}, {-0.22, 0.66}}];
line = Plot[{0.43 + 0.44*0.5/3 + 0.44*x/3}, {x, -0.5, 0.25}, PlotRange -> {{0, 0.6}}, Filling -> Bottom, FillingStyle -> Opacity[0.6]];
curve2 = Plot[{x - Exp[x - 0.05] + 1.5, 0.43 + 0.44*0.5/3 + 0.44*x/3}, {x, -0.5, 0.25}, PlotStyle -> Thick, Axes -> False, PlotRange -> {{-1.6, 0.6}, {0.0, 0.66}}, Filling -> {1 -> {2}}, FillingStyle -> Yellow];
ar1 = Graphics[{Black, Arrowheads[0.07], Arrow[{{-1.0, 0.0}, {0.6, 0.0}}]}];
t1 = Graphics[ Text[Style["f(t, y(t))", FontSize -> 12], {-0.7, 0.5}]];
xn = Graphics[ Text[Style[Subscript["x", "n"], FontSize -> 12, FontColor -> Black, Bold], {-0.48, -0.05}]];
xn1 = Graphics[ Text[Style[Subscript["x", "n+1"], FontSize -> 12, FontColor -> Black, Bold], {0.24, -0.05}]];
Show[curve, curve2, line, ar1, t1, xn, xn1]

To find its numerical solution, we pick up the uniform set of grid points \( x_n = x_0 + h\, n , \quad n=0,1,2,\ldots ; \) where the step size h is fixed for simplicity. As usual, we denote by yn approximate values of unknown function at mesh points \( y_n \approx \phi (x_n ) , \quad n=0,1,2,\ldots ; \) where ϕ is the actual solution of the given initial value problem (IVP for short).

The concept of the Trapezoidal Rule in numerical methods is similar to the trapezoidal rule of Riemann sums. The Trapezoid Rule is generally more accurate than the Euler approximations, and it calculates approximations by taking the sum of the function of the current and next term and multiplying it by half the value of h. Therefore the syntax will be as follows:

\begin{equation} \label{EqHeun.3} y_{n+1} = y_n + \frac{h}{2} [ f( x_n , y_n ) + f( x_{n+1} , y_{n+1} ) ] , \qquad n=0,1,2,\ldots . \end{equation}
This is an implicit one-step method: the value yn+1 appears on both sides of the equation, and to actually calculate it, we have to solve an equation which will usually be nonlinear. One possible method for solving this equation is Newton's method that was discussed in the section.

 

A one-step explicit numerical method leads to a difference equation for discrete approximate values of the solution. As a rule, a discrete problem has much reacher properties than its continuous counterpart. Sometimes long term calculations may lead either to divergent process (referred to as instability) or to stable numerical solution---called the ghost solution---that has nothing in common with expected solution to the IVP, as was shown in Euler section. To avoid the instability and to prevent the appearance of ghost solutions for the long range calculation, many refined numerical procedures to integrate the ordinary differential equations have been proposed. In practical calculations, the central difference scheme is used when evaluations of slope function in intermediate points (as, for instance, required by Runge--Kutta methods) are not permitted. We mention two remedies to remove ghost solutions.

Consider the following mixed difference scheme parameterized by μ, 0 <μ<1, for the first order differential equation:
\[ \left( 1 - \mu \right) \frac{y_{n+1} - y_{n-1}}{2h} + \mu\,\frac{y_{n+1} - y_n}{h} = f\left( x_n , y_n \right) , \qquad n=1,2,\ldots . \]
If we set μ = 1, then we have Euler's rule. When μ = 0, the scheme is simply the central difference scheme. This algorithm does not produce ghost solutions when μ > h/2.

Example: Consider the initial value problem for the linear equation

\[ \frac{{\text d}y}{{\text d}x} = y - 4\,e^{-3x} , \qquad y(0) = 1. \]
Its exact solution is \( y(x) = e^{-3x} . \)
DSolve[{y'[x] == y[x] - 4*Exp[-3*x], y[0] == 1 + e}, y[x], x]
{{y[x] -> E^(-3 x) (1 + e E^(4 x))}}
When we try to solve this equation numerically, we actually solve a pertubated problem
\[ \frac{{\text d}y}{{\text d}x} = y - 4\,e^{-3x} , \qquad y(0) = 1 + \epsilon , \]
where ϵ is a small number. The solution of such pertubed problem is
\[ y(x) = e^{-3x} + \epsilon\,e^{x} . \]
The appearance of the exponential term may cause a trouble leading to appearance of the ghost solution.    ■

 

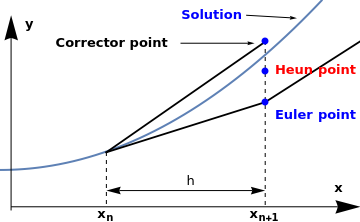
Heun's Formula / Improved Euler Method

The Improved Euler’s method, also known as Heun's formula or the average slope method, gives a more accurate approximation than the Euler rule and gives an explicit formula for computing yn+1. The basic idea is to correct some error of the original Euler's method. The syntax of the Improved Euler’s method is similar to that of the trapezoid rule, but the y value of the function in terms of yn+1 consists of the sum of the y value and the product of h and the function in terms of xn and yn.

   
curve = Plot[x^2 + 0.5, {x, 0.0, 1.7}, PlotStyle -> Thick, Axes -> True, PlotRange -> {{0.0, 1.7}, {-0.22, 2.8}}, Epilog -> {Blue, PointSize@Large, Point[{{1.25, 1.42}, {1.25, 1.83}, {1.25, 2.24}}]}];
line1 = Graphics[{Thickness[0.005], Line[{{0.5, 0.74}, {1.25, 1.42}, {2.0, 2.8}}], PlotStyle -> Black}];
line2 = Graphics[{Thickness[0.005], Line[{{0.5, 0.74}, {1.25, 2.24}}], PlotStyle -> Black}];
line2a = Graphics[{Dashed, Line[{{0.5, 0.74}, {0.5, 0.0}}]}];
line3a = Graphics[{Dashed, Line[{{1.25, 2.24}, {1.25, 0.0}}]}];
ar1 = Graphics[{Black, Arrowheads[{-0.04, 0.04}], Arrow[{{0.5, 0.22}, {1.25, 0.22}}]}];
h = Graphics[Text[Style["h", FontSize -> 12], {0.9, 0.35}]];
arx = Graphary = Graphics[{Black, Arrowheads[0.07], Arrow[{{0.05, -0.05}, {0.05, 2.60}}]}];
ary = Graphics[{Black, Arrowheads[0.07], Arrow[{{0.05, -0.05}, {0.05, 2.60}}]}];
x1 = Graphics[ Text[Style[Subscript["x", "n"], FontSize -> 12, FontColor -> Black, Bold], {0.5, -0.1}]];
x2 = Graphics[ Text[Style[Subscript["x", "n+1"], FontSize -> 12, FontColor -> Black, Bold], {1.25, -0.1}]];
x = Graphics[ Text[Style["x", FontSize -> 12, FontColor -> Black, Bold], {1.6, 0.25}]];
y = Graphics[ Text[Style["y", FontSize -> 12, FontColor -> Black, Bold], {0.14, 2.48}]];
euler = Graphics[ Text[Style["Euler point", FontSize -> 12, FontColor -> Blue, Bold], {1.49, 1.25}]];
heun = Graphics[ Text[Style["Heun point", FontSize -> 12, FontColor -> Red, Bold], {1.49, 1.85}]];
pr = Graphics[ Text[Style["Corrector point", FontSize -> 12, FontColor -> Black, Bold], {0.53, 2.22}]];
ar2 = Graphics[{Black, Arrowheads[0.02], Arrow[{{0.85, 2.22}, {1.2, 2.22}}]}];
s = Graphics[ Text[Style["Solution", FontSize -> 12, FontColor -> Blue, Bold], {1.4, 2.6}]];
ar3 = Graphics[{Black, Arrowheads[0.02], Arrow[{{1.16, 2.6}, {1.4, 2.56}}]}];
Show[curve, line1, line2, line2a, line3a, ar1, h, arx, ary, x1, x2, x, y, heun, euler, pr, ar2, s, ar3]
The improved Euler formula or the average slope method is commonly referred to as Heun's method (although discovered by C. Runge):
\begin{equation} \label{EqHeun.4} y_{n+1} = y_n + \frac{h}{2} [ f( x_n , y_n ) + f( x_{n+1} , y_n + h f( x_n , y_n ) ) ], \quad n=0,1,2,\ldots . \end{equation}
Since it is actually the simplest version of the predictor-corrector method (= Heun's method), the recurrence can be written as
\begin{equation} \label{EqHeun.5} \begin{split} p_{n+1} &= y_n + h\, f \left( x_n , y_n \right) , \\ y_{n+1} &= y_n + \frac{h}{2} [ f( x_n , y_n ) + f( x_{n+1} , p_{n+1} ) ], \quad n=0,1,2,\ldots . \end{split} \end{equation}

There are some versions of implementing of the Heun method with Mathematica. We demonstrate it on the IVP for the Riccati equation
\[ y' = x^2 + y^2 , \qquad y(0) = 1. \]
You can compare numerical solution with the explicit solution expressed through the Bessel functions:
\[ y(x) = x\,\frac{J_{-3/4} \left( \frac{x^2}{2} \right) \left( -\Gamma^2 \left( \frac{3}{4} \right) + \pi \right) + Y_{-3/4} \left( \frac{x^2}{2} \right) \Gamma^2 \left( \frac{3}{4} \right)}{J_{1/4} \left( \frac{x^2}{2} \right) \left( -\Gamma^2 \left( \frac{3}{4} \right) + \pi \right) + Y_{1/4} \left( \frac{x^2}{2} \right) \Gamma^2 \left( \frac{3}{4} \right)} , \quad x> 0. \]
Note the solution blows up at x ≈ 0.9698106539, where the denominator is zero. First version is based on RecurrenceTable command.
Clear[h, x, y, n, nstep, f]
nstep = 10;
f[x0_, y0_] := x0^2 + y0^2;
h = 0.1;
x0 = 0.0;
y0 = 1.0;
xy = Quiet@RecurrenceTable[
{

x[n + 1] == x[n] + h, x[0] == x0,
(* p[0] is just to conform to software's initalization *)
p[n + 1] == y[n] + h f[x[n], y[n]], p[0] == 0,
y[n + 1] == y[n] + h (f[x[n], y[n]] + f[x[n + 1], p[n + 1]])/2, y[0] == y0
},
{x, y}, {n, 0, nstep}, DependentVariables -> {x, y, p}]
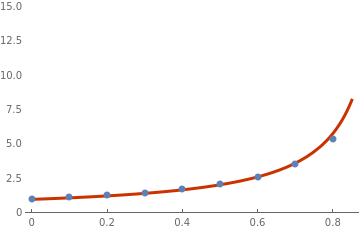
{0., 1.}, {0.1, 1.111}, {0.2, 1.25153}, {0.3, 1.43606}, {0.4, 1.68801}, {0.5, 2.04877}, {0.6, 2.60003}, {0.7, 3.52901}, {0.8, 5.37147}, {0.9, 10.3483}, {1., 38.1343}}
      Then we plot the discrete list {x,y}
list=ListPlot[xy, PlotStyle -> PointSize[Large], PlotRange -> {0, 15}]
s = NDSolve[{y'[x] == x^2 + (y[x])^2, y[0] == 1}, y, {x, 0, 0.85}]
plot = Plot[Evaluate[y[x] /. s[[1]]], {x, 0, 0.85}, PlotTheme -> "Web", PlotRange -> {0, 15}]
Show[plot, list]
       Figure 3: Discrete Heun points along with
       true solution. 		           Mathematica code

Or using Do loop: Clear[y]
f[x_, y_] := x^2 + y^2
y[0] = 1;
h:=0.1;
Do[k1 = h f[h n, y[n]];
k2 = h f[h (n + 1), y[n] + k1];
y[n + 1] = y[n] + .5 (k1 + k2),
{n, 0, 9}]
y[10]

The main difference here is that instead of using y[n+1]=y[n]+h*f(x[n],y[n]), we use

y[n+1]=y[n]+h/2(f(x[n],y[n])+f(x[n+1],y[n+1]))
For a built-in version of this, input the following:
heun[f_, {x0_, xn_}, {y0_}, steps_] :=
Block[{ xold = x0,
yold = y0,
sollist = {{x0, y0}}, h
},
h = N[(xn - x0) / steps];
Do[ xnew = xold + h;
k1 = h * (f /. {x -> xold, y -> yold});
k2 = h * (f /. {x -> xold + h, y -> yold + k1});
ynew = yold + .5 * (k1 + k2);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew,
{steps}
];
Return[sollist]
]

Instead of calculating intermediate values k1 and k2 , one can define ynew directly:

heun[f_, {x_, x0_, xn_}, {y_, y0_}, steps_] :=
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
ynew =
yold + (h/2)*((fold) + f /. {x -> xold + h, y -> yold + h*fold});
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]

The function heun is basically used in the same way as the function euler. Then to solve the above problem, do the following:

solution = heun[ x^2 + y^2 , {x, 0, 1}, {y, 1}, 10]

Then read the answer off the table.

Another option:

f[x_, y_] := Exp[2*x - y]
h = 0.1
K = IntegerPart[1.2/h]  (* if the value at x=1.2 needed *)
y[0] = 1                      (* initial condition *)

Then implement Heun's rule:

Do[y[n + 1] =
  y[n] + (h/2)*f[n*h, y[n]] + (h/2)*
    f[h*(n + 1), y[n] + h*f[n*h, y[n]]], {n, 0, K}]
y[K]

 

One iteration step of the Heun method can be coded as follows
oneHeun[args_] :=
Module[{f, x0, y0, predict0, correct0, x1, h, corrector, predictor, y1},
{f, y0, x0, predict0, correct0, h} = args;
{f, y1, x1, predictor, corrector, h}
];
Next, we make preparation for output (called "preprocessing" in computer science) in the different forms. So we make the reference (or association) to possible outputs: There is a special Mathematica command <| followed by |> . What is inside these two marks is the definition of references. You can find an interoduction to implementation of Associations on Wolfram websites:
https://www.wolfram.com/language/elementary-introduction/2nd-ed/34-associations.html
https://reference.wolfram.com/language/ref/Association.html
https://reference.wolfram.com/language/guide/Associations.html

We need often to have similar structure but no error issued if index is not available.
Association or <| |> addresses these issues and much more:

assoc = <|a -> x, b -> y, c -> z|>
assoc[0]
No error! Missing["KeyAbsent", 0]

In the following code, a return value variable called res
res=func[... ] ;

To figure out what is inside Association, use Keys:
Keys@res

{"list", "poly line”, “plot, “table””}
When you want to see its application, type
res["plot”] outputs the plot
heunNETLIST[args_, n_, syms_] :=
Module[{list, f, y0, x0, predict0, correct0, h, xy, tmp},
list = {};
{f, y0, x0, predict0, correct0, h} = args;
NestList[(AppendTo[list, {#, oneHeun[#]}]; oneHeun[#]) &, {f, y0, x0, predict0, correct0, h}, n];
xy = Table[{list[[i]][[1]][[3]], list[[i]][[1]][[2]]}, {i, 1, Length@list}];

<|

"list" -> list,
"poly line" -> xy,
"plot" ->
ListLinePlot[xy, PlotRange -> All, PlotTheme -> "Web", FrameLabel -> syms,
PlotLabel -> Row@{"Heun Solution to " <> syms[[2]] <> "'" <> "=", TraditionalForm@f[syms[[2]], syms[[1]]]}],
"table" -> (Dataset@Table[ tmp = Drop[list[[i]][[1]], 1];

<|
syms[[1]] -> tmp[[2]],
syms[[2]] -> tmp[[1]],
"predictor" -> tmp[[3]],
"corrector" -> tmp[[4]]

|>,

{i, 1, Length@list, 19}]),
"true solution" -> (
Block[{y, x, s},
y = ToExpression[syms[[2]]];
x = ToExpression[syms[[1]]];
s = NDSolve[{y'[x] == f[y[x], x], y[list[[1]][[1]][[3]]] == list[[1]][[1]][[2]]}, y, {x, list[[1]][[1]][[3]], n*h}];
Plot[ Evaluate[y[x00] /. s[[1]]], {x00, list[[1]][[1]][[3]], n*h}, PlotRange -> All]
]
)

|>

];

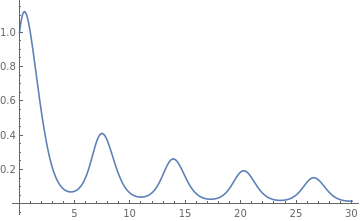
Example: Consider the initial value problem for the first order differential equation with oscillating slope function

\[ \frac{{\text d}y}{{\text d}t} = y\,\cos \left( t + y \right) , \qquad y(0) = 1. \]
We solve this IVP with Mathematica using previously described code heunNETLIST:
list = {};
f[y_, t_] := y*Cos[t + y];
h = 0.1; x0 = 0.0; y0 = 1;
predictor = y0 + h*f[y0, x0];
x1 = x0 + h;
corrector = y0 + h*(f[y0, x0] + f[predictor, x1])/2.0;
n = 300;

args = {f, y0, x0, corrector, predictor, h};
res = heunNETLIST[args, n, {"t", "y"}];

Keys@res
{"list", "poly line", "plot", "table"}

res["plot"]
res["true solution"]
     True solution.
res["table"]

t Heun solution Predictor NDSolve
0.0 1 1.04835 1.0
1.9 ??? ??? ???
   ■

Example: Consider the initial value problem for the first order differential equation with oscillating slope function

\[ \frac{{\text d}y}{{\text d}t} = \sin \left( t\,y \right)\cos \left( t + y \right) , \qquad y(0) = 1. \]
We solve this IVP with Mathematica using previously described code heunNETLIST:
list = {};
Clear[f];
f[y_, t_] := Sin[t*y]*Cos[t + y];
h = 0.1; x0 = 0.0; y0 = 1;
predictor = y0 + h*f[y0, x0];
x1 = x0 + h;
corrector = y0 + h*(f[y0, x0] + f[predictor, x1])/2.0;
n = 300;

args = {f, y0, x0, corrector, predictor, h};
res = heunNETLIST[args, n, {"t", "y"}];
res["plot"]
res["true solution"]
     True solution.
res["table"]
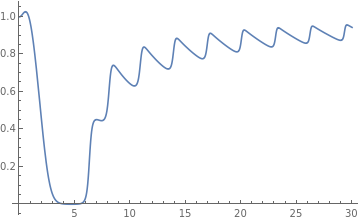
t Heun solution Predictor NDSolve
0.0 1 1.00226 1.0
1.9 0.500292 0.500263 ???
   ■

Example: Consider the initial value problem for the linear equation

\[ \frac{{\text d}y}{{\text d}x} = x\,y - x^2 , \qquad y(0) = 1. \]
First, we find its explicit solution
DSolve[{y'[x] == x*y[x] - x^2 , y[0] == 1}, y[x], x]
{{y[x] -> 1/2 (2 E^(x^2/2) + 2 x - E^(x^2/2) Sqrt[2 \[Pi]] Erf[x/Sqrt[2]])}}
\[ y(x) = e^{x^2 /2} + x - \sqrt{\frac{\pi}{2}}\,e^{x^2 /2} \mbox{erf}\left( \frac{x}{\sqrt{2}}\right) = e^{x^2 /2} + x - e^{x^2 /2} \int_0^x e^{-t^2}\,{\text d}t , \]
where erf(z) is the error function
\[ \mbox{erf} (z) = \frac{2}{\sqrt{\pi}}\,\int_0^z e^{-t^2}\,{\text d}t . \]
Heun's algorithm tells us that we first need to determine a predictor term
\[ p_{n+1} = y_n + h \left[ f\left( x_n , y_n \right) \right] = y_n + h \left[ \left( x_n \, y_n - x_n^2 \right) \right] = y_n \left( 1 + h\,x_n \right) -h x_n^2 , \]
and then use it to get the approximation from the corrector step:
\[ c_{n+1} = y_n + h \,f\left( x_{n+1} , p_{n+1} \right) = y_n + h \, x_{n+1} p_{n+1} - h\,x_{n+1} . \]
Taking their average, we get the Heun point:
\[ y_{n+1} = \frac{1}{2} \left( p_{n+1} + c_{n+1} \right) = y_n + \frac{h\,y_n}{2} \left( x_n^2 + h\,x_n + x_n \right) - \frac{h}{2} \left( x_n^3 + h\,x_n^2 + 2\,x_n^2 + 2h\,x_n + h^2 \right) \]
because xn+1 = xn + h. At each step, the Heun method requires 24 arithmetic operations to be performed, while Euler's rule needs only 6 arithmetic operations.    ■

Example: Consider the initial value problem for the logistic equation

\[ \frac{{\text d}y}{{\text d}t} = y\left( 3 - y \right) , \qquad y(0) = 1. \]
First, we find its explicit solution.
DSolve[{y'[t] == y[t]*(3 - y[t]), y[0] == 1}, y[t], t]
{{y[x] -> (3 E^(3 t))/(2 + E^(3 t))}}
\[ y(t) = \frac{3\, e^{3t}}{2+ e^{3t}} . \]
Choosing a uniform grid of points 0 = t0 < t1 < t2 < · · ·, we denot by yn the approximate value of y(tn) at mesh point tn according to Heun's algorithm.    ■

Example: Consider the initial value problem for the Riccati equation

\[ y' = y^2 - x^2 , \qquad y(0) = 1/2 . \]
Application of heun routine, we get
heun[y^2 - x^2, {0, 1}, {0.5}, 10]
{{0, 0.5}, {0.1, 0.525781}, {0.2, 0.552362}, {0.3, 0.577872}, {0.4, 0.600205}, {0.5, 0.616952}, {0.6, 0.625329}, {0.7, 0.622127}, {0.8, 0.603696}, {0.9, 0.566016}, {1., 0.504902}}
Therefore, heun's approximation yields y(0.5) ≈ 0.616952, which very close to the true value 0.617769.    ■

Example: Consider the initial value problem \( y'= 1/(3x-2y+1),\quad y(0)=0 \)

First, we find its solution using Mathematica's command DSolve:

f[x_, y_] := 1/(3 x - 2 y + 1)
DSolve[{y'[x] == f[x, y[x]], y[0] == 0}, y[x], x]
Out[2]= {{y[x] -> 1/6 (1 + 9 x - 2 ProductLog[1/2 E^(1/2 + (9 x)/2)])}}

To evaluate the exact solution at x=1.0, we type

a := DSolve[{y'[x] == f[x, y[x]], y[0] == 0}, y[x], x]
y[x] /. a /. x -> 1.0
Out[4]= {0.614275}

Then we use Heun's numerical method with step size h=0.1:

y[0] = 0; x[0] = 0; h = 0.1;
Do[k1 = h f[n*h, y[n]]; k2 = h f[h*(n + 1), y[n] + k1];
y[n + 1] = y[n] + 0.5*(k1 + k2), {n, 0, 9}]
y[10]
out[7]= 0.617265

Now we demonstrate the use of while command:

x[0] = 0; y[0] = 1; Nsteps =20;
i = 1
h=0.1;
Array[x, Nsteps];
Array[y, Nsteps];
While[i < Nsteps+1, x[i] = x[i - 1] + h; i++];
k=1
While[k < Nsteps,
y[k] = y[k - 1] + (h/2)*
Function[{u, v}, f[u, v] + f[u + h, v + h*f[u, v]]][x[k - 1], y[k - 1]];
k++];
Array[y, Nsteps]     (* to see all Nsteps values *)
y[Nsteps]                (* to see the last value *)
   ■

Example: Let us take a look at the initial value problem for the integro-differential equation

\[ \dot{y} = 2.3\, y -0.01\,y^2 -0.1\,y\, \int_0^t y(\tau )\,{\text d}\tau , \qquad y(0) =50. \]
First, we recall y1 found previously based on Euler rule that we use as a predictor:
\[ p_1 = 50 +2.3\,h\,50 -0.01\,h \,50^2 - 0.1\,h^2 \,50^2 . \]
Now we correct this value based on trapezoid rule:
\[ y_1 = 50 + \frac{h}{2} \left[ 2.3\left( 50 + p_1 \right) -0.01\left( 50^2 + p_1^2 \right) \right] -0.1 \, \int_0^h \,{\text d}\tau \,\int_{\tau}^h {\text d}s \, y(s)\,y(\tau ) . \]
We approximate again the double integral in the right hand-side with the trapezoid rule:
\[ T_1 (h) = \int_0^h \,{\text d}\tau \,\int_{\tau}^h {\text d}s \, y(s)\,y(\tau ) \approx \frac{h}{2} \, \int_0^h {\text d}s \, y(s)\,y(0 ) \approx \frac{h^2}{4} \, y(0) \left[ p_1 + y(0) \right] = 12.5\,h^2 \left[ 50 + p_1 \right] . \]
Therefore,
\[ y_1 = 50 + \frac{h}{2} \left[ 2.3\left( 50 + p_1 \right) -0.01\left( 50^2 + p_1^2 \right) \right] - 1.25\,h^2 \left[ 50 + p_1 \right] . \]
    ■

 

Numerical experiment with iterations

The general case of Heun's method yields
\[ \begin{split} p_{k+1} &= y_k + 2.3\,h\,y_k -0.01\,h\,y^2_k -0.1 \, y_k \,h\, T_k (h) ,\qquad k=1,2,\ldots ; \qquad t_{k+1} = t_k +h , \\ y_{k+1} &= y_k + \frac{h}{2} \left[ 2.3\left( y_k + p_{k+1} \right) -0.01\left( y^2_k + p_{k+1}^2 \right) \right] -0.1\,T_{k+1} (h) , \\ &= y_k + \frac{h}{2} \, 2.3 \left( y_k + p_{k+1} \right) - \frac{h}{2} \, 0.01 \left( y_k^2 + p_{k+1}^2 \right) - \frac{h}{20} \left[ y_k\, \int_0^{t_k} y(\tau )\,{\text d}\tau + p_{k+1}\, \int_0^{t_{k+1}} y(\tau )\,{\text d}\tau \right] \end{split} \]
where
\[ T_{k} (h) = \int_0^{t_k} {\text d} s\, \int_s^{t_k} {\text d} \tau\, y(s)\,y(\tau ) = \int_0^{t_k} {\text d} \tau \, \int_0^{\tau} {\text d} s\,y(s)\,y(\tau ) , \quad k=1,2,\ldots . \]
We break the integral into sum
\[ T_{k+1} (h) = T_k (h) + \int_{t_k}^{t_{k+1}} {\text d} \tau \, \int_0^{\tau} {\text d} s\,y(s)\,y(\tau ) = T_k (h) + \int_{t_k}^{t_{k+1}} {\text d} s \, \int_s^{t_{k+1}} {\text d} \tau\,y(s)\,y(\tau ) + \int_{t_k}^{t_{k+1}} {\text d} \tau \, \int_0^{t_k} {\text d} s\,y(s)\,y(\tau ) . \]
Using again the trapezoid rule, we get
\begin{align*} T_{k+1} (h) &= T_k (h) + \frac{h}{2}\, y_k \,\int_{t_k}^{t_{k+1}} {\text d} \tau \,y( \tau ) + \frac{h}{2} \left[ p_{k+1} \int_0^{t_{k}} {\text d}s \,y(s) + y_k \int_0^{t_{k}} {\text d}s \,y(s) \right] \\ &= T_k (h) + \frac{h^2}{4} \,y_k \left[ p_{k+1} + y_k \right] + \frac{h}{2} \left( p_{k+1} + y_k \right) \int_0^{t_{k}} {\text d}s \,y(s) . \end{align*}
The integral in the right hand-side can be iterated:
\[ J_k = \int_0^{t_{k}} {\text d}s \,y(s) = \int_0^{t_{k-1}} {\text d}s \,y(s) + \int_{t_{k-1}}^{t_{k}} {\text d}s \,y(s) = J_{k-1} + \int_{t_{k-1}}^{t_{k}} {\text d}s \,y(s) \approx J_{k-1} + \frac{h}{2} \left( y_k + y_{k-1} \right) , \]
with \( J_1 = \frac{h}{2} \left( y_1 + 50 \right) . \) Now we ask Mathematica to do calculations.
h = 0.01
y[0] =50

 

Heun's method: To approximate the solution of the initial value problem \( y' = f(x,y), \ y(a ) = y_0 \) over [a,b] by computing
\[ y_{n+1} = y_n + \frac{h}{2} \left[ f(x_n , y_n ) + f\left( x_{n+1} , y_n + h\,f(x_n , y_n ) \right) \right] , \qquad n=0,1,2,\ldots , m-1. \]

 

Make a computational experiment: in the improved Euler algorithm, using the corrector value as the next prediction, and only after the second iteration use the trapezoid rule.

The ``improved'' predictor-corrector algorithm:

\[ \begin{align*}
k_1 &= f(x_k , y_k ) ,
\\
k_2 &= f(x_{k+1} , y_k + h\,k_1 ) ,
\\
k_3 &= y_k + \frac{h}{2} \left( k_1 + k_2 \right) ,
\\
y_{k+1} &= y_k + \frac{h}{2} \left( k_1 + k_3 \right) ,
\end{align*} \]
is realized using the following Mathematica script:

heunit[f_, {x_, x0_, xn_}, {y_, y0_}, steps_] :=
  Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
  h = N[(xn - x0)/steps];
  Do[xnew = xold + h;
   k1 = f[xold, yold];
   k2 = f[xold + h, yold + k1*h];
   k3 = yold + .5*(k1 + k2)*h;
   ynew = yold + .5*(k1 + f[xnew, k3])*h;
   sollist = Append[sollist, {xnew, ynew}];
   xold = xnew;
   yold = ynew, {steps}];
  Return[sollist]]

Then we apply this code to numerically solve the initial value problem \( y' = (1+x)\,\sqrt{y} , \quad y(0) =1 \) with step size h=0.1:
f[x_, y_] = (1 + x)*Sqrt[y]
heunit[f, {x, 0, 2}, {y, 1}, 20]
we get approximate value 9.00778 while the regular Heun's method gives 8.99148.

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Pr