Preface
Mathematical models utilized to describe population growth evolved, undergoing several modifications after Malthus’ model (1798). One of the most important and well known models was proposed by the Belgium sociologist P. F. Verhulst (1838). In this model, it is assumed that all populations are prone to suffer natural inhibitions in their growths, with a tendency to reach a steady limit value as time increases. Another important proposal was developed by Montroll (1971), which consists of a general model, that translates the asymptotic growth of a variable taking into account the position of the inflection point of the curve.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part II of the course APMA0330
Glossary


Population Models
Growth or decay is a common occurrence in many systems ranging from biology to economics. Since mathematical language is more concise and less ambiguous than any natural language, the biological models were revised leading to the proposal of a variety of growth curves and the theoretical frameworks that lay behind them. Due to environmental trends and fluctuation, probably no biologist believes that one equation would suit all growth processes. This situation is completely different from those that we observe in physics, where usually only one law is used. For instance, modeling of the fall of a body in a vacuum requires only one of Newton's laws. In many systems, growth patterns are ultimately subjected to some form of limitation. In practice, we usually observe a set of measured values Yt, at some time sequence { t }, called a time series. Modeling these observations means finding a curve P(t) that is closed to the time series. For example, to model a US population growth, we deal with an equally spaced time series, based on the census, conducted every ten years.
In this section, we discuss some simple models that are expressed solely in terms of differential equations of the first order that ignore random fluctuations in the population. Such models are referred to as deterministic and they are written as
Malthus and Doomsday models of population growth
With developing mathematical methods, biologists started in the late 18th century to use these techniques in population modeling in order to understand the dynamics of growing and shrinking populations of living organisms. Thomas Malthus (1766--1834) was one of the first to note that populations grow with a geometric pattern (dP/dt = r P) while contemplating the fate of humankind. The Malthus model leads to exponential (unbounded) growth, which is clearly not viable in the long-term run:
In 1960, H. von Foerster, P.M. Mora, and L.W.Amiot proposed a Doomsday model:
Von Foerster and his colleagues present many examples of accepted models of physical systems with singularities: pressure as a function of velocity approaching the speed of sound, current approaching breakdown voltage in gaseous conduction, index of refraction in optical absorption bands, and magnetic susceptibility at Curie temperature in ferromagnetism. It is reasonable to expect a singular behavior of a social structure subjected to extreme overpopulation. Nevertheless, the doomsday model provides a remarkably good fit of practical examples for certain time intervals.
Another fundamental growth mode is one subjected to limitations that affect growth rates, making growth slow down over time and asymptotically strive towards a maximum value. Growth may actually continue interminably but the rate of growth approaches zero as time tends to infinity. This is well-known in many biological systems where an organism may grow quickly in its juvenile stage but then growth slows down as it reaches maturity. Bounded growth curves can be used to model renewable energy sources since some kind of upper limit must exist even for renewable energy. Rather in the growth process itself, the limiting factor lies in the form of the increasing monetary, energy, or resource costs required for continued expansion. The upper limit may be high, or virtually non-existent, but the steps in development become more and more challenging to take, thus slowing the growth process. In the biological sciences, this is often seen as proportionality between growth rate and actual size or age.
Logistic model of population growth
Usually, we never observe such exponential growth in long time run because of limitation of resources. Therefore, the Malthus model can be used only for relatively short period of time. ■
One of the most basic and milestone models of population growth was the logistic model of population growth formulated by Pierre François Verhulst in 1838. (We don't know why Verhulst called this equation logistic, but this name is universally accepted.) An outstanding exposition of its history is given by G. Evelyn Hutchinson (1903--1991) in his book, published in 1978. The logistic model (\( \dot{P} = r\,P \left( 1 - P/K \right) \) ) takes the shape of a sigmoid curve and describes the growth of a population. He observed that if species are not preyed upon, its population is expected to saturate. Its solution is
| U.S. Population and logistic population growth | |||||
|---|---|---|---|---|---|
| Year(t) | Actual Population | Value of P(t) | Year(t) | Actual Population | Value of P(t) |
| (in millions) | (in millions) | ||||
| 1800 (0) | 5.308 | 5.30 | 1900 (100) | 72.212 | 79.61 |
| 1810 (10) | 7.239 | 7.11 | 1910 (110) | 92.228 | 98.33 |
| 1820 (20) | 9.638 | 9.52 | 1920 (120) | 106.021 | 119.08 |
| 1830 (30) | 12.866 | 12.71 | 1930 (130) | 122.775 | 141.14 |
| 1840 (40) | 17.069 | 16.90 | 1940 (140) | 132.164 | 163.59 |
| 1850 (50) | 23.192 | 22.38 | 1950 (150) | 150.697 | 185.45 |
| 1860 (60) | 31.443 | 29.44 | 1960 (160) | 179.323 | 205.82 |
| 1870 (70) | 38.558 | 38.42 | 1970 (170) | 203,392 | 224.05 |
| 1880 (80) | 50.189 | 49.63 | 1980 (180) | 226.545 | 239.78 |
| 1890 (90) | 62.979 | 63.33 | 1990 (190) | 248.709 | 252.94 |
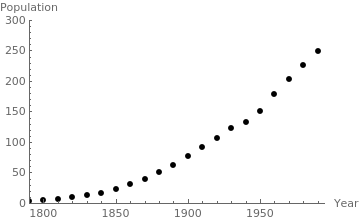
|
census =
{{1790, 3.929}, {1800, 5.308}, {1810, 7.239}, {1820, 9.638}, {1830, 12.866},{1840, 17.069}, {1850, 23.192}, {1860, 31.443}, {1870, 38.558}, {1880, 50.189}, {1890, 62.979}, {1900, 72.212}, {1910, 92.228}, {1920, 106.021}, {1930, 122.775}, {1940, 132.164}, {1950, 150.697}, {1960, 179.323}, {1970, 203.392}, {1980, 226.545}, {1990, 248.709}};
Now we introduce the final time
tf = 1990;
and plot the data
censusgraph = ListPlot[census, AxesLabel->{"Year", "Population"}, AxesOrigin->{1790, 0}, PlotRange->{{1790, tf+5},{0, 300}}, PlotStyle-> {Black, PointSize[0.02]}]
|
First, we solve the logistic equation with the Bernoulli method by representing its solution as the product P = u v, where u is a solution of the separable equation
We solve this equation with Mathematica:
NSolve[p0^2 *(K/3.929 - 1)*(K/7.239 - 1) == (K - p0)^2, K]
r = (1/10)*Log[p0/(K - p0)*(K/3.929 - 1)]
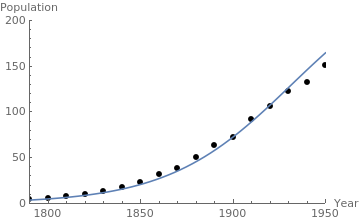
|
census = {{1790, 3.929}, {1800, 5.308}, {1810, 7.239}, {1820,
9.638}, {1830, 12.866}, {1840, 17.069}, {1850, 23.192}, {1860,
31.443}, {1870, 38.558}, {1880, 50.189}, {1890, 62.979}, {1900,
72.212}, {1910, 92.228}, {1920, 106.021}, {1930, 122.775}, {1940,
132.164}, {1950, 150.697}, {1960, 179.323}, {1970,
203.392}, {1980, 226.545}, {1990, 248.709}};
censusgraph = ListPlot[census, AxesLabel -> {"Year", "Population"}, AxesOrigin -> {1790, 0}, PlotRange -> {{1790, 1995}, {0, 300}}, PlotStyle -> {Black, PointSize[0.02]}]; r = 0.03; y0 = 5.308; lineplot = Plot[0.145/(0.00056 + 0.039*Exp[-0.03*(t - 1790)]), {t, 1790, 1950}]; Show[censusgraph, lineplot] |
Since that time, there has been substantial progress in developing mathematical population models. Obviously, we cannot discuss and analyze a huge variety of population models. Instead, we present some famous models involving one ordinary differential equation. More complicated cases involving interaction of spices require a usage of system of differential equations, and this topic is covered in the second part of the tutorial.
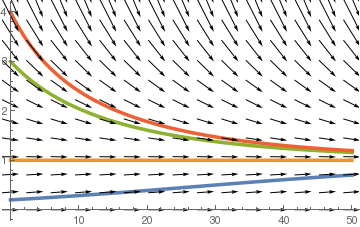
|
field = VectorPlot[{1, P/20*(1 - P/2) - 0.1*P^2/(3 + P^2)}, {t, 0,
50}, {P, 0, 5}, VectorScale -> {0.05, 0.8, 1 &},
VectorStyle -> Black, FrameStyle -> Gray, Background -> LightGray, FrameLabel -> {t, P}, PlotLegends -> {"time", "Population"}, DisplayFunction -> Identity]; n1 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 0.2}, P[t], {t,0,50}]; n2 = NDSolve[{P;'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 1}, P[t], {t,0,50}] n3 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 3}, P[t], {t,0,50}]; n4 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 4}, P[t], {t,0,50}]; solplot = Plot[Evaluate[P[t]/.{n1,n2,n3,n4}], {t,0,50}, PlotStyle->Thickness[0.01]]; Show[solplot,field] |
The same graphs can be obtained using command Map.
solplot2 = Plot[Evaluate[P[t] /. numsol2], {t, 0, 10}, PlotStyle -> Thickness[0.01], DisplayFunction -> Identity]
The following two population models mimic features of asexual and sexual reproduction. The asexual reproduction model is of the form:
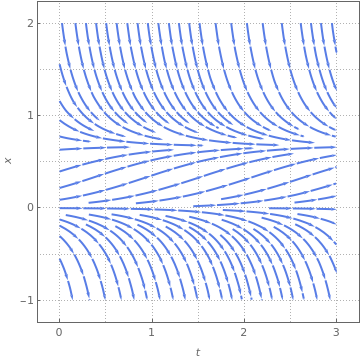
StreamPlot[{1, 0.3*x*(1 - x) - x}, {t, 0, 3}, {x, -1, 2}, FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Business"]
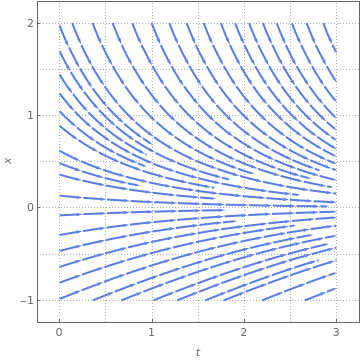
StreamPlot[{1, 3*x*x*(1 - x) - x}, {t, 0, 3}, {x, -3, 3}, FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Web"]
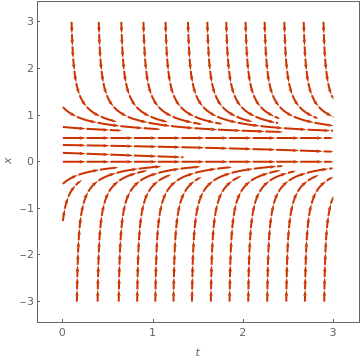
StreamPlot[{1, 10*x*x*(1 - x) - x}, {t, 0, 3}, {x, -0.4, 1.2}, FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Web"]
|
|
|
|
The above direction field plots allow us to determine the behavior of solutions near critical points; some of them are asymptotically stable, some only semi-stable, and others are unstable. In each case, the variable x represents a scaled population size and the parameter 𝑎 is assumed to be positive. Both slope functions have the critical point x=0. However, the function f has an additional equilibrium point x=1-1/ 𝑎, while the function g may have two more equilibrium points:
The slope function g(x) has two critical points, and the derivative at point \( x_{-}^{\ast} \) is negative for 𝑎>4; therefore, this point is asymptotically stable. The derivative of g(x) at another critical point \( x_{+}^{\ast} \) is positive for 𝑎>4. On the other hand, these two critical points disappear for 𝑎<4. So the point 𝑎=4 is a saddle-node bifurcation point. ■
Dynamics of a harvested population
Consider the dynamics of a harvested population for the logistic equation
Constant harvesting
The two simplest harvesting models are constant harvesting rate and proportional harvesting rate. We start with the former. Suppose \( h(P) = h_0 \) is a constant. Then the slope function becomes
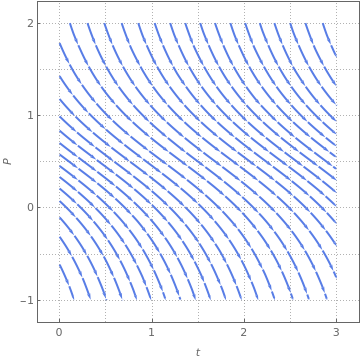
|
|
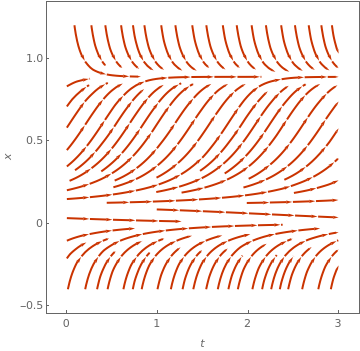
StreamPlot[{1, 1*x*(1 - x) - 1}, {t, 0, 3}, {x, -1, 2},
FrameLabel -> {t, P}, MeshStyle -> {Thick}, PlotTheme -> "Business"]
StreamPlot[{1, 5*x*(1 - x) - 1}, {t, 0, 3}, {x, -0.4, 1.2}, FrameLabel -> {t, P}, MeshStyle -> {Thick}, PlotTheme -> "Web"] |
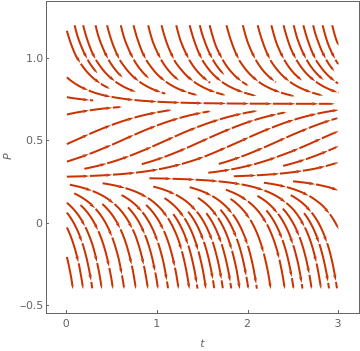
By rescaling the population u = P/K, time \( \tau = r\,t , \) and harvesting rate \( h = h_0 /rK , \) we arrive at the equation
The proportional harvesting model is, after non-dimensionalization, of the form:
|
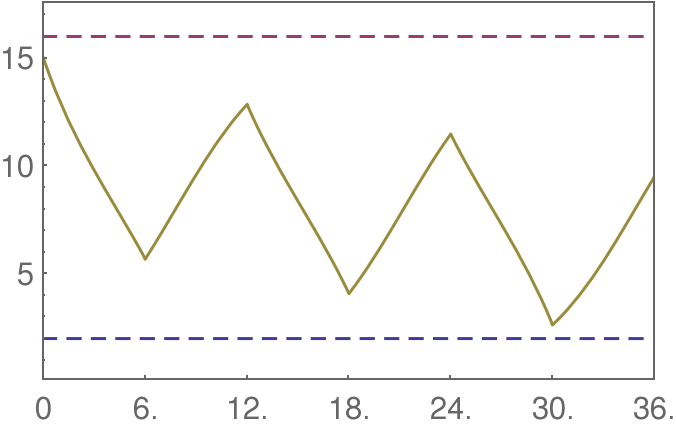
T = 6.0; (* time interval length *)
ER = 8/3.; (* extraction rate *) L = 16; (* carrying capacity *) k = 1/3; (* exponential rate *) b = 2.; (* low threshold *) y1[1] = 15.; (* initial population *) nT = 3; (* number of time cycles *) Do[ soln1[i] = DSolve[{y'[x] == k y[x] (1 - y[x]/L) - ER, y[(2 i - 2) T] == y1[i]}, y[x], x] // Quiet // Flatten; y2[i] = y[x] /. soln1[i] /. x -> T (2 i - 1); soln2[i] = DSolve[{y'[x] == k y[x] (1 - y[x]/L), y[(2 i - 1) T] == y2[i]}, y[x], x] // Quiet // Chop // Flatten; y1[i + 1] = y[x] /. soln2[i] /. x -> T (2 i); , {i, 1, nT}]; mytable = Table[{{y[x] /. soln1[i], (2 i - 2) T <= x < (2 i - 1) T}, {y[x] /. soln2[i], (2 i - 1) T <= x < (2 i) T}}, {i, 1, nT}]; myfun[x_] = Piecewise[Partition[Flatten[mytable], 2]]; Plot[{b, L, myfun[x]}, {x, 0, nT 2 T}, PlotRange -> {{0, nT 2 T}, {0.1, 1.1 L}}, Frame -> True, PlotStyle -> {Dashing[0.02], Dashing[0.02], Automatic}, FrameTicks -> {T Range[0, 2 nT], Automatic, None, None}, AxesOrigin -> {0, 0}] |
Rational model for harvesting
One defect of the constant harvesting rate model is that P = 0 is not a fixed point. To remedy this, consider the following model for the harvesting rate:
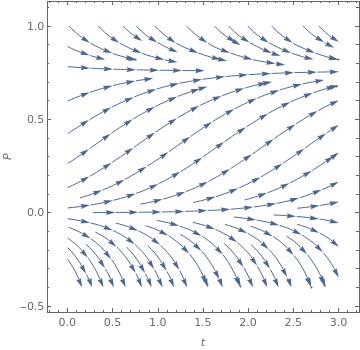
|
StreamPlot[{1, 2*x*(1 - x) - x*x/(1 + x*x)}, {t, 0, 3}, {x, -0.4, 1},
FrameLabel -> {t, P},
StreamStyle -> Arrowheads[{{0.03, Automatic}}],
MeshShading -> {Red, None}]
|
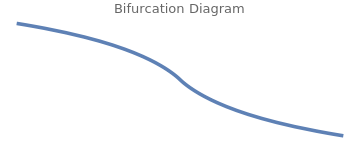
There is an unstable fixed point at n = 0, where g'(0) = γ > 0. The other fixed points occur when the term in the brackets vanishes. We seek the intersection of the harvesting function \( h(n) = n/(n^2 + 1) \) with a two-parameter family of straight lines, given by \( y(n) = \gamma \left( 1- n/c \right) . \) The n-intercept is c and the y-intercept is γ. Provided c > c* is large enough, there are two bifurcations as a function of γ, which we call \( \gamma_{\pm} (c) . \)
Both bifurcations are of the saddle-node type. We determine the curves \( \gamma_{\pm} (c) \) by requiring that h(n) is tangent to y(n), which gives two equations:
|
ParametricPlot[{2*n^3/(n^2 - 1), 2*n^3/(n^2 + 1)^2}, {n, -0.6, 0.6},
Axes -> False, PlotStyle -> {Thickness[0.01]},
PlotLabel -> "Bifurcation Diagram"]
|
Since h(n) is maximized for n = 1, where \( h(1) = \frac{1}{2} , \) there is no bifurcation occurring at value n < 1. If we plot γ(c) versus c(n) over the allowed range of n, we obtain the phase diagram. The cusp occurs at \( \left( c^{\ast} , \gamma^{\ast} \right) , \) and is determined by the requirement that the two bifurcations coincide. This supplies a third condition, namely that the second derivative is zero:
Population model with a threshold
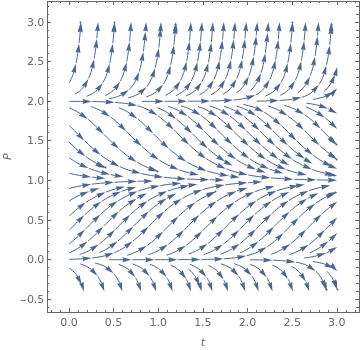
|
StreamPlot[{1, 3*x*(1 - x)*(2 - x)}, {t, 0, 3}, {x, -0.4, 3},
FrameLabel -> {t, P},
StreamStyle -> Arrowheads[{{0.03, Automatic}}],
MeshShading -> {Red, None}]
|
Gompertz's model

Benjamin's model is also known as the Gompertz theoretical law of mortality. He fitted it to the relationship between increasing death rate and age, what he referred to as “the average exhaustions of a man’s power to avoid death”, or the “portion of his remaining power to oppose destruction”. The insurance industry quickly started to use his method of projecting death risk. However, Gompertz only presented the probability density function. It was W.M. Makeham who first stated this model in its well-known cumulative form, and thus it became known as the Gompertz--Makeham model.
Separation of variables in the Gompertz equation yields
Next exponentiation yields the explicit formula for the Gompertz's curve:
Another re-parameterisation of the Gompertz model can also be written as the three parameter curve:
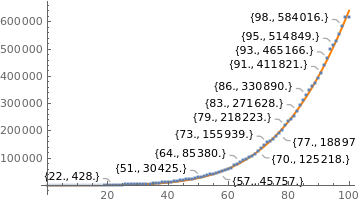
we apply Gompertz's model
totalcases = {1 , 1, 1 , 1 , 2 , 2 , 2, 2, 3, 8, 13, 13, 25, 25, 34, 52 , 77, 98, 121, 200, 234, 291, 428, 621, 904, 1128, 1546 , 1891, 2201 , 2433 , 2915 , 3417 , 3904 , 4256 , 4579 , 5717 , 6836 , 7910 , 9056 , 10278, 11130 , 12056 , 13717 , 15927 , 17857 , 19638 , 20727 , 22169 , 23430, 25262 , 28320 , 30425 , 33682 , 36599 , 38654, 40581 , 43079 , 45757, 49492 , 52995 , 58509 , 61888 , 71886 , 78162 , 85380 , 91589 , 96559 , 101147 , 107780, 114715 , 125218 , 135106 , 145328 , 155939, 162699 , 168331, 177589 , 188974 , 202918, 218223 , 233142, 241080, 254220, 271628 , 291579 , 310087 , 330890 , 347398 , 363211 , 374898 , 391222, 411821, 438238, 465166 , 498440, 514849 , 526447, 555383, 584016 , 614941 , 614941};
data = Thread[{dayssincefirstcase, totalcases}];
realdata = ListPlot[data, PlotStyle -> Large, LabelingFunction -> Callout[Automatic]];
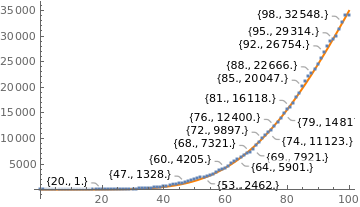
totald = {0 , 0 , 0 , 0 , 0 , 0, 0, 0, 0 , 0, 0, 0, 0 , 0, 0, 0 , 0, 0, 0 , 0, 1 , 4 , 6 , 11, 18, 25, 34, 46 , 57 , 77 , 92 , 114, 136, 159, 201, 241 , 299 , 359, 432, 486, 553, 667, 800, 941, 1056, 1124, 1223, 1328, 1532, 1736, 1924, 2141, 2347, 2462, 2575, 2741, 2906 , 3313 , 3670 , 4016 , 4205, 4543, 5017, 5466, 5901, 6329, 6750, 7025, 7321, 7921, 8536, 9146, 9897, 10627, 11123, 11519 , 12400 , 13149 , 13993, 14817, 15633, 16118 , 16792, 17971, 18859 , 20047 , 21048 , 22013 , 22666, 23473 , 24512 , 25598, 26754, 27878, 28834, 29314, 29937, 31199 , 32548, 34021, 34021};
datad = Thread[{dayssincefirstcase, totald}];
reald = ListPlot[datad, PlotStyle -> Large, LabelingFunction -> Callout[Automatic]]
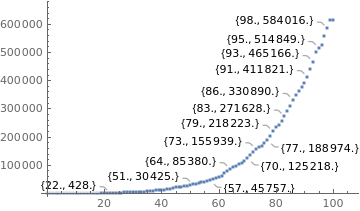
|
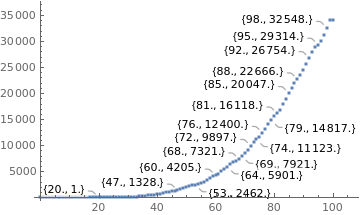
|
|
K = 1.2630463902640887*10^7; a = 12.70849421908572; r = 0.0145;
gompertz = Plot[g[0.0145, t], {t, 0, 100}, PlotStyle -> {Thick, Orange}]; realdata = ListPlot[data, PlotStyle -> Large, LabelingFunction -> Callout[Automatic]]; Show[gompertz, realdata] |
|
dayssincefirstcase = {0, 1 , 2, 3, 4 , 5 , 6 , 7, 8, 9, 10, 11, 12,
13, 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 ,
26 , 27, 28 , 29, 30 , 31 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 ,
40 , 41 , 42 , 43 , 44, 45, 46 , 47 , 48 , 49 , 50 , 51 , 52 ,
53, 54 , 55 , 56 , 57 , 58 , 59 , 60 , 61 , 62 , 63 , 64 , 65 ,
66 , 67 , 68 , 69 , 70 , 71 , 72 , 73, 74, 75, 76 , 77, 78 , 79,
80, 81 , 82 , 83 , 84 , 85 , 86 , 87 , 88 , 89, 90 , 91 , 92, 93,
94 , 95, 96 , 97, 98, 99, 100};
totald = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 4, 6, 11, 18, 25, 34, 46, 57, 77, 92, 114, 136, 159, 201, 241, 299, 359, 432, 486, 553, 667, 800, 941, 1056, 1124, 1223, 1328, 1532, 1736, 1924, 2141, 2347, 2462, 2575, 2741, 2906, 3313, 3670, 4016, 4205, 4543, 5017, 5466, 5901, 6329, 6750, 7025, 7321, 7921, 8536, 9146, 9897, 10627, 11123, 11519, 12400, 13149, 13993, 14817, 15633, 16118, 16792, 17971, 18859, 20047, 21048, 22013, 22666, 23473, 24512, 25598, 26754, 27878, 28834, 29314, 29937, 31199, 32548, 34021, 34021}; datad = Thread[{dayssincefirstcase, totald}]; reald = ListPlot[datad, PlotStyle -> Large, LabelingFunction -> Callout[Automatic]]; NonlinearModelFit[datad, K*Exp[-a*Exp[-r*t]], {K, a, r}, t] K = 128239.9181316305; a = 14.346820302208794; r = 0.024; gompertz = Plot[g[0.024, t], {t, 0, 100}, PlotStyle -> {Thick, Orange}]; reald = ListPlot[datad, PlotStyle -> Large, LabelingFunction -> Callout[Automatic]]; Show[gompertz, reald] |
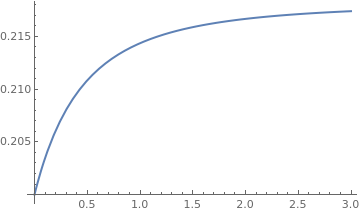
The Korf model
The Korf differential equation is easy to solve by separating variables.
|
b = 2.3;
NN[t_] = 0.2*Exp[0.2/b*(1 - 1/(1 + t)^b)] Plot[NN[t], {t, 0, 3}, PlotStyle -> Thick] |
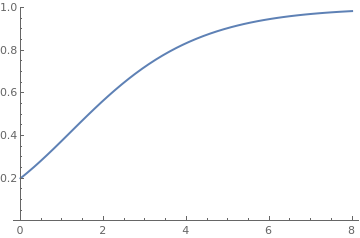
The Richards curve
Since the Richards equation is an example of a more general Bernoulli equation, we seek its solution in the form of the product R(t) = u(t) v(t), where u(t) is a solution of the truncated linear equation
|
P[t_] = Exp[2*t]/(-1 + Exp[2*t*0.3] + (1/0.2)^0.3)^(10/3)
Plot[P[t], {t, 0, 8}, PlotRange -> {0, 1}, PlotStyle -> Thick] |
| Coronavirus cases in Sweden | ||||||
|---|---|---|---|---|---|---|
| Days (March 1 corresponds to 1) | Actual Cases: Sweden | Predicted Value of P(t) | Days (March 1 corresponds to 1) | Actual Cases: Sweden | Predicted Value of P(t) | |
| 1 | 14 | 61 (April 30) | 21092 | |||
| 5 | 94 | 65 (May 4) | 22721 | |||
| 9 (March 9) | 260 | 69 (May 8) | 25265 | |||
| 13 (March 13) | 814 | 73 (May 12) | 27272 | |||
| 17 (March 17) | 1196 | 77 (May 16) | 29677 | |||
| 21 (March 21) | 1770 | 81 (May 20) | 31523 | |||
| 25 (March 25) | 2526 | 85 (May 24) | 33459 | |||
| 29 (March 29) | 3770 | 89 (May 28) | 35727 | |||
| 33 (April 2) | 5568 | 93 (June 1) | ||||
| 37 (April 6) | 7206 | 97 (June 5) | ||||
| 41 (April 10) | 9685 | 101 (June 9) | ||||
| 45 (April 14) | 11445 | 105 (June 13) | ||||
| 49 (April 18) | 13822 | 109 (June 17) | ||||
| 53 (April 22) | 16004 | 113 (June 21) | ||||
| 57 (April 26) | 18640 | 117 (June 25) | ||||
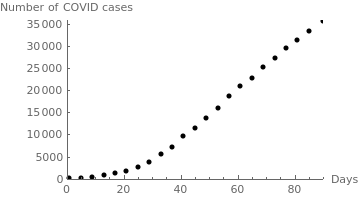
|
sweden = {{1,15}, {5,94}, {9,260}, {13,814}, {17, 1196}, {21,1770}, {25,2526}, {29,3700}, {33, 5568}, {37,7206},{41,9685}, {45,11445}, {49,13822},{53,16004},{57,18640}, {61,21092}, {65,22721},{69,25265}, {73,27272},{77,29677},{81,31523},{85,33459}, {90,35727}};
censusgraph = ListPlot[sweden, AxesLabel -> {"Days", "Number of COVID cases"}, AxesOrigin -> {0, 0}, PlotRange -> {{0, 90}, {0, 36000}}, PlotStyle -> {Black, PointSize[0.02]}]; |
Using Mathematica we try to determine the numerical values of parameters in the Richards model.
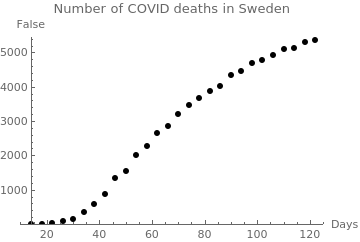
|
swed = {{14, 2},
{18, 10},
{22, 21},
{26, 77},
{30, 146},
{34, 353},
{38, 591},
{42, 887},
{46, 1333},
{50, 1540},
{54, 2021},
{58, 2274},
{62, 2653},
{66, 2854},
{70, 3220},
{74, 3460},
{78, 3679},
{82, 3871},
{86, 4029},
{90, 4350},
{94, 4468},
{98,4704},
{102,4782}, {106,4939}, {110,5106},{114,5118},{118,5295},{122,5375}};
censusgraph = ListPlot[swed, AxesLabel -> {"Days", False}, PlotLabel -> "Number of COVID deaths in Sweden", AxesOrigin -> {14, 0}, PlotRange -> {{10, 125}, {0, 5450}}, PlotStyle -> {Black, PointSize[0.02]}] |
Weibull growth model
Assuming[ gamma > 0, Simplify[%]]
https://www.worldometers.info/coronavirus/country/italy/
https://www.worldometers.info/coronavirus/country/south-africa/
| Coronavirus cases for two countries: Italy and South Africa | |||||
|---|---|---|---|---|---|
| Days (March 1 corresponds to 1) | Actual Cases: Italy | Predicted Value of P(t) | Actual Cases: South Africa | Predicted Value of P(t) | |
| 1 | 1701 | 0 | |||
| 5 | 3858 | 1 | |||
| 9 | 9172 | 7 | |||
| 13 | 17,660 | 24 | |||
| 17 | 31,506 | 85 | |||
| 21 | 53,578 | 240 | |||
| 25 | 74,386 | 709 | |||
| 29 | 97,689 | 1,280 | |||
| 33 (April 2) | 115,242 | 1,686 | |||
| 37 (April 6) | 132,547 | 1,686 | |||
| 41 (April 10) | 147,577 | 2,003 | |||
| 45 (April 14) | 162,488 | 2,415 | |||
| 49 (April 18) | 175,925 | 3,034 | |||
| 53 (April 22) | 187,327 | 3,635 | |||
| 57 (April 26) | 197,675 | 4,546 | |||
| 61 (April 30) | 205,463 | 5,647 | |||
| 65 (May 4) | 211,938 | 7,220 | |||
| 69 (May 8) | 217,185 | 8,895 | |||
| 73 (May 12) | 221,216 | 11,350 | |||
| 77 (May 16) | 224,760 | 14,355 | |||
| 81 (May 20) | 227,364 | 18,003 | |||
| 85 (May 24) | 229,858 | 22,583 | |||
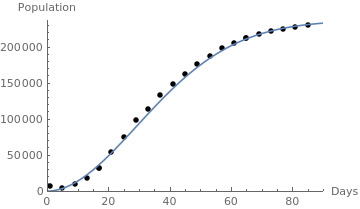
|
italy = {{1,7011}, {5,3858}, {9,9172}, {13,17660}, {17, 31506}, {17,31596}, {21,53578}, {25,74386}, {29, 97689}, {33,113242},{37,132547}, {41,147577}, {45,162488},{49,175925},{53,187327}, {57,197675}, {61,205463},{65,211938}, {65,211938},{69,217185},{73,221216},{77,224760}, {81,227364},{85,229858}};
censusgraph = ListPlot[italy, AxesLabel -> {"Days", "Population"}, AxesOrigin -> {0, 0}, PlotRange -> {{0, 90}, {0, 237000}}, PlotStyle -> {Black, PointSize[0.02]}]; beta = 0.00075; gamma = 23/12; W0=237000; lineplot = Plot[ Exp[-beta*t^(gamma)] + W0*(1 - Exp[-beta*t^(gamma)]), {t, 0, 90}]; Show[censusgraph, lineplot] |
Janoschek growth model
The von Bertalanffy model
In 1934, he was habilitated by Reininger, Schlick and the zoologist Versluys for the first volume of his Theoretische Biologie. The monography postulated two essential aims of a theoretical biology, firstly to clean up the conceptual terminology of biology, and, secondly, to explain how the phenomena of life can spontaneously emerge from forces existing inside an organism. Here the organismic system represented the main problem as well as the still-to-be-formulated program of a theoretical biology. The second volume developed the research program of a dynamic morphology and applied the mathematical method to biological problems.
As a Rockefeller Fellow at the University of Chicago (1937-38), he worked with the Russian physicist Nicolaus Rashevsky. There he gave his first lecture about the General System Theory as a methodology that is valid for all sciences (1949). In 1939 he was appointed to an extraordinary professor at the University of Vienna. There Bertalanffy concentrated his research on a comparative physiology of growth. He was the first biologist who held lectures in zoology for students of medicine and an integrated course on botany and zoology. During this time he wrote an article about organisms as physical systems (1940), the summary of his biological reasoning: Problems of Life.
In 1949, Ludwig emigrated to Canada where he mainly worked on metabolism, growth, biophysics, and cancer cytology. In his biomedical research on cancer he developed, with his son Felix, the Bertalanffy-method of cancer cytodiagnosis. From the 1950's onwards he shifted his research from the biological sciences to the methodology of science, the General System Theory (GST), and cognitive psychology. Based on his humanistic world view, he developed a holistic epistemology (1966) which sharply criticized the machine metaphor of neobehaviorism (Robots).
In 1960 Ludwig was appointed a Professor of the Department of Zoology and Psychology at the University of Alberta in Edmonton (Canada). There Bertalanffy, the psychologist Royce and the philosopher Tenneysen established the Advanced Center for Theoretical Psychology that became a center for cognitive psychology over the next 30 years. In that time his systematic theoretical approach focused on the modern world of technology and has thrown us humans out of nature and has isolated us from each other. Bertalanffy emphasized in his later works the importance of the symbolic worlds of culture which we ourselves have created during evolution.
After his retirement, he became a Professor of the Faculty of Social Sciences at the State University of New York (SUNY). An international symposium celebrated his 70th birthday in 1971. In June 1972, he suffered a heart stroke and died a few days later, on June 12, shortly after midnight.
To sum up his life-work, Bertalanffy wrote 13 monographies, four anthologies, and over 200 articles, He was the chief editor of the Handbuch der Biologie--among many others. His themes encompassed theoretical biology and experimental physiology (Bertalanffy equations), theoretical psychology--particularly in the last two decades of his life, cancer research (Bertalanffy method of cancer cytodiagnosis), and philosophy and history of science. No doubt, the person Bertalanffy was a very fascinating one, proud of his European background, a connoisseur of architectural drawings, Japanese woodcuts, and stamps, who loved to hear the music of Mozart and Beethoven and to become absorbed in the works of Goethe. Sometimes he puzzled his environment by sarcastic remarks, or his black sense of humor. His worldview was an old-fashioned one, however, never outdated that was deeply rooted in a humanistic ethos:
In the last resort, however, it is always a system of values, of ideas, of ideologies - choose whatever word you like - that is decisive. (1964)Bertalanffy (1957) derived his equation from the assumptions, which he attributed to Pütter (1920), that the rate of anabolism is proportional to the surface area of an organism (or to its mass raised to the power of ⅔), while catabolism is proportional to the organism's mass. Von Bertalanffy formulation (1957) of the equation is based on the biological principles of anabolism and catabolism, that is, growth and destruction. He derived his equation from the assumptions, which he attributed to Pütter (1920), that the rate of anabolism is proportional to the surface area of an organism (or to is mass raised to the power of ⅔), while catabolism is proportional to the organism's mass. The Bertalanffy model is often used as a population model to study the factors that control and affect its growth. It is used to describe the populations of fish, animals, such as pigs, horses, cattle, sheep, etc. It is also suitable for modelling tumors and infectious diseases because it is similar to the growth of individuals and populations:
Since the Bertalanffy equation is a Bernoully equation, we solve it by representing the solution in the form of the product of two functions: P(t) = u(t) v(t). Here u(t) is a solution of the truncated linear part:
Solve[P'[t] == 0, {t}]
|
|
Plot[x^(2/3) - x, {x, 0, 1}, PlotStyle -> Thick]
P[t_] = Exp[-2*t/1]*(1*Exp[2*t/3/1] - 1 + 0.1^(1/3))^3 Plot[P[t], {t, 0, 8}, PlotRange -> {0, 1}, PlotStyle -> Thick] |
To capture the dynamics of harvesting a population or tumour treatment we can add a harvesting term E(t) P(t). Here, E is also considered to vary with time and represents harvesting effort. Adding this term to the Bertalanffy population model results in a new harvesting IVP,
U-Bertalaffy:
The von Bertalanffy (1957) growth law can be written as
Spruce Budworm population
The spruce budworm is an insect which is a serious threat to forests. In 1978, Ludwig, Jones, and Holling published a paper in which they proposed an ingenious model of the interaction of the insects, the trees, and the predatory birds. They proposed that the budworm population P obeys a logistic model modified by a predation rate:
The analysis of the above equation for P(t) can be simplified by introducing dimensionless variables \( t=a\tau \) and P = by, where \( a= k/\beta \) and b = k. Then the equation can be written in the following form:
The interpretation of the above equation is both simple and important. Its left-hand side is per capita growth rate of the scaled variable y (with respect to a scaled time). The right-hand side is per capita death rate due to predation, also in scaled variables. The points where these curves intersect are nonzero equilibria for y.

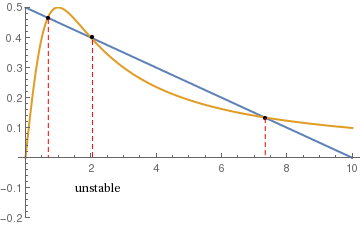
Two critical points are stable and the middle is unstable. |
R = 0.5; A = 0.1;
a = Plot[{R*(1 - A*y), y/(1 + y*y)}, {y, 0, 10}, PlotStyle -> {Thick}, Epilog -> Text[Style["unstable", 10, FontFamily -> Times], {2.2, -0.1}], PlotRange -> {-0.2, 0.5}] b = ListPlot[{{0.7, 0.465}, {2.05, 0.4}, {7.34, 0.132}}, PlotStyle -> {Large, Black}] line1 = Line[{{0.7, 0.46}, {0.7, 0}}] line2 = Line[{{2.05, 0.39}, {2.05, 0}}] line3 = Line[{{7.34, 0.13}, {7.34, 0}}] c = {Graphics[{Dashed, Red, line1}], Graphics[{Dashed, Red, line2}], Graphics[{Dashed, Red, line3}]} Show[a, b, c] |
The critical values of R and A are where two roots coalesce and disappear. The bifurcation points are obtained from the following system of equations:
- Bass F, 1969. A new product growth model for consumer durables. Management Science, 15, 215–227.
- Cabrera, N.V., Jafelice, R.S.M., Bertone, A.M., Montroll’s model applied to a population growth data set using type-1 and type-2 fuzzy parameters, Biomatematica, 2016, Vol. 26, pp. 145--160.
- Goel, N. S., Maitra, S. C., Montroll, E. W., On the Volterra and other nonlinear models of interacting populations. Reviews of Modern Physics, 1971, Vol. 43, pp. 231--276. https://doi.org/10.1103/RevModPhys.43.231
- Gompertz B, 1825. On nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London, 115, 513–585.
- Hutchinson, G.E., An introduction to population ecology, Yale University Press, New Haven, CT, 1978, 260p.
- Janoschek A, 1957. Das reaktionskinetische Grundgesetz und seine Beziehungen zum Wachstums- und Ertragsgesetz. Statistische Vierteljahresschrift, 10, 25–37.
- Karev, G.P., Non-linearity and heterogeneity in modelling of population dynamics, Mathematical Biosciences, 258 (2014), pp. 85-92.
- Kiviste, A.K., Mathematical functions of forest growth. Estonian Agricultural Academy, 1988, Tartu. 108 p + Supplement 171 p. (In Russian).
- Korf, V., Contribution to the mathematical definition of forest stands growth. (Příspěvek k matematické definici vzrůstového zákona hmot lesních porostů). Lesnická práce, 1939, Vol. 18, pp. 339--379 (In Czech).
- Ludwig, D., Jones, D.D., and Holling, C.S., Journal of Animal Ecology, 1978, 47, Issue 1, 315--332.
- Makeham, W.M., On the integral of Gompertz's function for expressing the values of sums depending upon the contingency of life, Journal of the Institute of Actuaries and Assurance Magazine, 1873, Vol. 17, No. 5, pp. 305--327.
- Montroll, E. W. and West, B.J., Models of Population Growth, Diffusion, Competition and Rearrangement, In: Haken H. (eds) Synergetics. Vieweg+Teubner Verlag, Wiesbaden, 1973, pp 143--156; doi: https://doi.org/10.1007/978-3-663-01511-6_12
- Panik, M.J., Growth Curve Modeling: Theory and Applications, Wiley, 2014.
- Richards, F.J., A flexible growth curve for empirical use. Journal of Experimental Botany, 1959, Vol. 10, No. 29, pp. 290--300.
- Smith, D.A., Human population growth: Stability or Explosion?, Mathematics Magazine, 1977, Vol. 50, No. 4, pp. 186--197. https://www.jstor.org/stable/23686557
- Thieme, H., Mathematics in Population Biology, Princeton: Princeton Univer-sity Press, 2003.
- Tsoularis, A., Wallace, J., 2002. Analysis of logistic growth models. Mathematical Biosciences, 179(1), 21–55.
- Verhulst, P.F., 1838. Notice sur la loi que la population suit dans son accroissement. Correspondence Mathematique et Physique, 10, 113–121.
- von Bertalanffy, L, Problems of organic growth, Nature, 1949, , vol. 163, no.4135, pp. 156-158. doi:10.1038/163156a0
- von Foerster, H., Mora, P.M., Amiot, L.W., Doomsday, Friday, 13 November, A.D. 2026, Science, 1960, , vol. 132, pp. 1291--1295.
- Weibull, W., 1951. A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18(3), 293–297.
- Zeide, B., Analysis of growth equations, Forest Science, 1993, Vol. 39, No. 3, pp. 594--616.
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value
Problems)