Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part IV of the course APMA0330
Glossary
Applications
We present some applications of differential equations of order greater than one.
Example: (Flow Problem) A 500 liter container initially contains 10 kg of salt. A brine mixture of 100 grams of salt per liter is entering the container at 6 liter per minute. The well-mixed contents are being discharged from the tank at the rate of 6 liters per minute.
Express the amount of salt in the container as a function of time.
Salt is coming at the rate: 6*(0.1)=0.6 kg/min
d yin /dt =0.6 ; d yout/dt = 6x/500
dx/dt = 0.6 -6x/500 ; x(0)=10
DSolve[{x'[t]==6/10-6*x[t]/500, x[0]==10},x[t],t]
Out[15]= {{x[t] -> 10 E^(-3 t/250) (-4 + 5 E^(3 t/250))}}
Suppose that the rate of discharge is reduced to 5 liters per minute.
DSolve[{x'[t]==6/10-5*x[t]/(500+t), x[0]==10},x[t],t]
SolRule[t_] = Apart[x[t] /. First[%]]
SolRule[t_] = Apart[x[t] /. First[%]]
Out[1]= {{x[t] -> (1/(
10 (500 + t)^5))(3125000000000000 + 187500000000000 t +
937500000000 t^2 + 2500000000 t^3 + 3750000 t^4 + 3000 t^5 + t^6)}}
Out[2]= 50 + t/10 - 1250000000000000/(500 + t)^5
To check the answer: Simplify[SolRule'[t] == 6/10 - 5*SolRule[t]/(500 + t)]
Together[SolRule'[t] == Together[6/10 - 5*SolRule[t]/(500 + t)]]
SolRule[0]
Together[SolRule'[t] == Together[6/10 - 5*SolRule[t]/(500 + t)]]
SolRule[0]
Out[3]= True
Out[4]= True
Out[5]= 10
■ Out[4]= True
Out[5]= 10
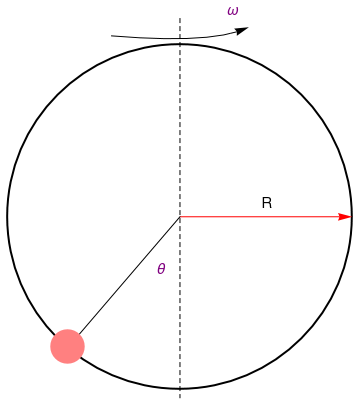
Example: Consider a bead of mass m on a rotating hoop of radius R.
circle = Graphics[{Thick, Circle[{0, 0}, 1]}]
disk = Graphics[{Pink, Disk[{-0.65, -0.75}, 0.1]}]
linev = Graphics[{Dashed, Line[{{0, 1.15}, {0, -1.05}}]}]
line = Graphics[Line[{{0, 0}, {-0.6, -0.7}}]]
ar = Graphics[ Arrow[BezierCurve[{{-0.4, 1.05}, {0.2, 1}, {0.4, 1.1}}]]]
arrow = Graphics[{Red, Arrow[{{0, 0}, {1, 0}}]}]
text1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Purple], {-0.11, -0.3}]]
text2 = Graphics[ Text[Style["\[Omega]", FontSize -> 14, Purple], {0.31, 1.2}]]
text3 = Graphics[Text[Style["R", FontSize -> 14, Black], {0.5, 0.08}]]
Show[circle, arrow, ar, line, linev, disk, text1, text2, text3]
disk = Graphics[{Pink, Disk[{-0.65, -0.75}, 0.1]}]
linev = Graphics[{Dashed, Line[{{0, 1.15}, {0, -1.05}}]}]
line = Graphics[Line[{{0, 0}, {-0.6, -0.7}}]]
ar = Graphics[ Arrow[BezierCurve[{{-0.4, 1.05}, {0.2, 1}, {0.4, 1.1}}]]]
arrow = Graphics[{Red, Arrow[{{0, 0}, {1, 0}}]}]
text1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Purple], {-0.11, -0.3}]]
text2 = Graphics[ Text[Style["\[Omega]", FontSize -> 14, Purple], {0.31, 1.2}]]
text3 = Graphics[Text[Style["R", FontSize -> 14, Black], {0.5, 0.08}]]
Show[circle, arrow, ar, line, linev, disk, text1, text2, text3]
disk2 = Graphics[{Pink, Disk[{0.65, -0.75}, 0.1]}];
linev2 = Graphics[{Dashed, Line[{{0, 1.0}, {0, -1.0}}]}];
line2 = Graphics[Line[{{0, 0}, {0.6, -0.7}}]];
tilt = Graphics[{Dashed, Line[{{0.25, 0.97}, {-0.3, -1.2}}]}];
ar2 = Graphics[ Arrow[BezierCurve[{{-0.5, -1.3}, {-0.0, -1.55}, {-0.1, -1.1}}]]];
rAngls = {{0.7, {-11.4*Pi/8, 10.33*Pi/6}}};
directives = {Directive[Red, Thick, Arrowheads[{{-0.05, 0}, {0.05, 1}}]]};
arcsWArrows[args1 : {{_, {_, _}} ..}, dir_List: {Directive[GrayLevel[.3], Arrowheads[{{-0.05, 0}, {0.05, 1}}]]}] :=
ParametricPlot[
Evaluate[#[[1]]*{Cos[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]],
Sin[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]]} & /@ args1], {u, 0, 2 Pi}, PlotStyle -> dir, Axes -> False, PlotRangePadding -> .2, ImageSize -> 200] /. Line[x_, ___] :> Arrow[x]
ar3 = arcsWArrows[rAngls, {directives[[1]]}];
text1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Purple], {0.21, -0.80}]];
text2 = Graphics[ Text[Style["\[Omega]", FontSize -> 14, Purple], {0.1, -1.3}]];
text4 = Graphics[ Text[Style["\[Alpha]", FontSize -> 14, Black], {0.1, 0.85}]];
Show[circle, arrow, ar2, line2, linev2, disk2, text1, text2, text3, text4, tilt, ar3]
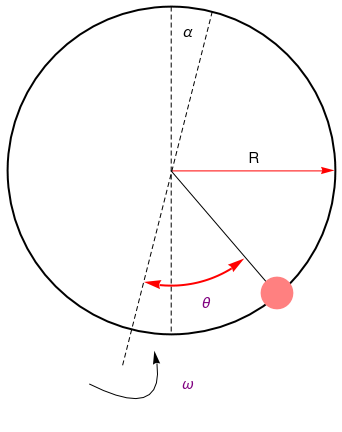
linev2 = Graphics[{Dashed, Line[{{0, 1.0}, {0, -1.0}}]}];
line2 = Graphics[Line[{{0, 0}, {0.6, -0.7}}]];
tilt = Graphics[{Dashed, Line[{{0.25, 0.97}, {-0.3, -1.2}}]}];
ar2 = Graphics[ Arrow[BezierCurve[{{-0.5, -1.3}, {-0.0, -1.55}, {-0.1, -1.1}}]]];
rAngls = {{0.7, {-11.4*Pi/8, 10.33*Pi/6}}};
directives = {Directive[Red, Thick, Arrowheads[{{-0.05, 0}, {0.05, 1}}]]};
arcsWArrows[args1 : {{_, {_, _}} ..}, dir_List: {Directive[GrayLevel[.3], Arrowheads[{{-0.05, 0}, {0.05, 1}}]]}] :=
ParametricPlot[
Evaluate[#[[1]]*{Cos[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]],
Sin[Rescale[u, {0, 2 Pi}, Abs@#[[2]]]]} & /@ args1], {u, 0, 2 Pi}, PlotStyle -> dir, Axes -> False, PlotRangePadding -> .2, ImageSize -> 200] /. Line[x_, ___] :> Arrow[x]
ar3 = arcsWArrows[rAngls, {directives[[1]]}];
text1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Purple], {0.21, -0.80}]];
text2 = Graphics[ Text[Style["\[Omega]", FontSize -> 14, Purple], {0.1, -1.3}]];
text4 = Graphics[ Text[Style["\[Alpha]", FontSize -> 14, Black], {0.1, 0.85}]];
Show[circle, arrow, ar2, line2, linev2, disk2, text1, text2, text3, text4, tilt, ar3]
 |
 |
The kinetic energy reads
\[
\mbox{K} = \frac{1}{2}\,m R^2 \left( \dot{\theta}^2 + \sin^2 \theta \,\omega^2 \right) .
\]
The potential energy is
\[
\Pi = -mgR \left( \cos\alpha \,\cos \theta + \sin \alpha \,\cos \omega t \,\sin \theta \right) ,
\]
where θ is the angle measured from the bottom of the hoop with respect to the direction of the rotation axis and α is the angle formed between the rotation axis and the vertical direction. If there exist a friction, which could be modeled by the force
\[
{\bf F} = - c{\bf v} ,
\]
which leads to the generalised force
\[
Q = -c R^2 \dot{\theta} \qquad\mbox{since} \quad {\bf v} = R\dot{\theta} .
\]
Inserting these xpressions into the Lagrangian \( L = \mbox{K} - \Pi , \) and aplying the Euler--langange equations, we obtain the equation of motion:
\[
\ddot{\theta} + \frac{c}{m}\,\dot{\theta} + \left( \frac{g}{R}\,\cos\alpha - \omega^2 \cos\theta \right) \sin \theta = \frac{g}{R} \,\sin \alpha \,\cos\theta \,\cos \omega t .
\]
If the tilt angle α is small, the above equation can be linearized in α by natural substitution:
\[
\ddot{\theta} + \frac{c}{m}\,\dot{\theta} + \left( \frac{g}{R} - \omega^2 \cos\theta \right) \sin \theta = \frac{g}{R} \, \alpha \,\cos\theta \,\cos \omega t .
\]
If rotation is along vertical axis (α = 0), we get a homogeneous differential equation
\[
\ddot{\theta} + \frac{c}{m}\,\dot{\theta} + \left( \frac{g}{R} - \omega^2 \cos\theta \right) \sin \theta = 0.
\]
The equilibrium positions θ = θ*, associated to the condition that θ and its velocity are both zeroes, are obtained by solving either
\[
\sin \theta =0 \qquad\mbox{or} \qquad \frac{g}{R} - \omega^2 \cos\theta =0 ,
\]
This gives three physical stationary points:
\[
\theta^{\ast} = 0, \quad \pi , \quad \arccos \left( \frac{g}{\omega^2 R} \right) ,
\]
subject to condition
\[
\omega \ge \omega_c = \sqrt{\frac{g}{R}} .
\]
Therefore, if the angular velocity of the hoop ω is greater than a critical angular velocity ωc, we observe the third critical point; otherwise thare are only two of them. This situation indicates that we observe a supercritical pitchfork bifurcation about the stationary value ωc.
line = Graphics[{Thick, Line[{{0, 0}, {1, 0}}]}];
curve1 = Plot[Sqrt[x - 1], {x, 1, 3.5}, PlotStyle -> {Thick, Black}];
curve2 = Plot[-Sqrt[x - 1], {x, 1, 3.5}, PlotStyle -> {Thick, Black}];
line2 = Graphics[{Thick, Dashed, Line[{{3.8, 0}, {1, 0}}]}];
text1 = Graphics[ Text[Style["stable", FontSize -> 14, Purple], {0.5, 0.1}]];
text2 = Graphics[ Text[Style["unstable", FontSize -> 14, Purple], {2.5, 0.1}]];
Show[text1, text2, line, line2, curve1, curve2, FrameLabel -> {"\[Omega]/\!\(\*SubscriptBox[\(\[Omega]\), \(c\)]\)", None}, Frame -> True, GridLines -> Automatic]
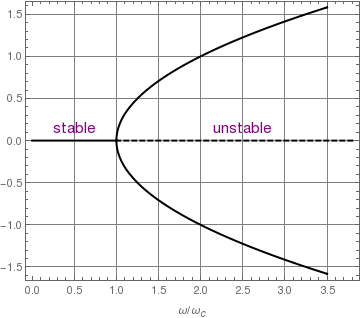
curve1 = Plot[Sqrt[x - 1], {x, 1, 3.5}, PlotStyle -> {Thick, Black}];
curve2 = Plot[-Sqrt[x - 1], {x, 1, 3.5}, PlotStyle -> {Thick, Black}];
line2 = Graphics[{Thick, Dashed, Line[{{3.8, 0}, {1, 0}}]}];
text1 = Graphics[ Text[Style["stable", FontSize -> 14, Purple], {0.5, 0.1}]];
text2 = Graphics[ Text[Style["unstable", FontSize -> 14, Purple], {2.5, 0.1}]];
Show[text1, text2, line, line2, curve1, curve2, FrameLabel -> {"\[Omega]/\!\(\*SubscriptBox[\(\[Omega]\), \(c\)]\)", None}, Frame -> True, GridLines -> Automatic]
Example:
Example: Move to chapter 4, application4 Consider the Lane--Emden type equation with an exponential nonlinearity of the solution with respect to the variable base
\[
\frac{{\text d}^2 y}{{\text d}x^2} + \frac{2}{x}\, \frac{{\text d}y}{{\text d}x} + (x+1)^{y(x)}, \qquad y(0) =1, \quad y' (0) =0.
\]
■ Example: Consider the initial value problem for undamped Duffing equation:
\[
y'' + k\, y =0, \qquad y(0) = \varepsilon \,y^3 , \quad y' (0) =0.
\]
We can rewrite the Duffing equation in the operator form:
\[
L\left[ y \right] \equiv \texttt{D}^2 y = N \left[ y \right] \equiv
\varepsilon \,y^3 - k\, y.
\]
Physically, the resilience of the oscillator is directly proportional to
N[y]. When k ≥ 0 and ε < 0, there is one
unique equilibrium point y = 0 where the nonlinear term vanishes.
However, when k ≤ 0 and ε > 0, there are two
equilibrium points: y = 0 and
\( y = \sqrt{|k/\varepsilon |} . \)
From the physical points of view, the sum of the kinetic and
potential energy of the oscillator keeps the same, therefore it is clear that
the oscillation motion is periodic, no matter k is positive or
negative. Thus, from physical points of view, it is easy to know that
y(t) is periodic, even if we do not directly solve the Dufing
equation.
■ - Raviola, Lisandro A., Veliz, Maximiliano E., Salomone, Horacio D., Olivieri, Nestor A., and Rodriguez, Eduardo E. The bead on a rotating hoop revisited: an unexpected resonance, European Journal of Physics, 38, 2017, 015005 (13pp).
- Halloun I.A. and Hestenes D., Common sense concepts about motion, American Journal of Physics, 53, 1985, 1056
- Perez F., Granger B.E., and Hunter J.D., Python: an ecosystem for scientific computing, Computing in Science & Engineering, Volume: 13, Issue: 2, 2011, pages: 13--21. doi: 10.1109/MCSE.2010.119
- Sivardiere J., A simple mechanical model exhibiting a spontaneous symmetry breaking, American Journal of Physics, 51, 1983, 1016 https://doi.org/10.1119/1.13362
- Drugowich de Felicio J.R. and Hipolito O., Spontaneous symmetry breaking, American Journal of Physics, 53, 1985, 690
- Ochoa F. and Clavijo J., Bead, hoop, and spring as a classical spontaneous symmetr breaking problem, European Journal of Physics, 27, 2006, 1277
- Rousseaux G., Bead, hoop, and spring ...: some theoretical remarks, European Journal of Physics, 28, 2007, L7--9
- Mancuso R.V., A working mechanical model for first- and second-order phase transition and the cusp catastrope, American Journal of Physics, 68, 2000, 271
- Cross R., Coulomb's law for tolling friction, American Journal of Physics, 84, 2016, 221
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)