Preface

This section presents derivation of simple pendulum equation.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part IV of the course APMA0330

Glossary

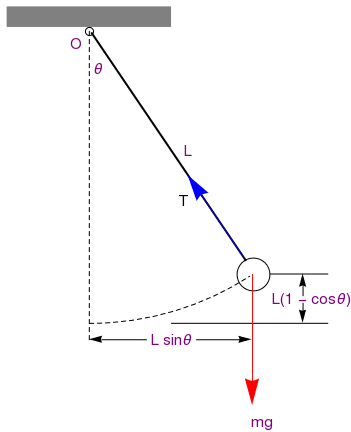
Simple Pendulum

The motion of the pendulum is, evidently, completely characterized by the variable θ, measured in counterclockwise direction as positive. We call θ the generalized coordinate for this system. It arises because the motion is constrained by \( x^2 + y^2 = \ell^2 . \) Even though the pendulum swings in 3 dimensional space, its motion is characterized by a single variable. We say in this case that the pendulum has “one degree of freedom.”

polygon = Polygon[{{-1, 0}, {1, 0}, {1, 1/4}, {-1, 1/4}}];
top = Graphics[{Gray, polygon}];
circle1 = Graphics[Circle[{0, -1/20}, 1/20]];
circle2 = Graphics[Circle[{2, -3}, 1/5]];
circle3 = Graphics[{Dashed, Circle[{0, 0}, 3.6, {-1.57, -1.0}]}];
line1 = Graphics[{Dashed, Line[{{0, -1/20}, {0, -3.8}}]}];
line2 = Graphics[{Thick, Line[{{0.03, -0.07}, {1.9, -2.83}}]}];
arrow = Graphics[{Red, Arrowheads[0.08], Arrow[{{1.986, -3.0}, {1.986, -4.6}}]}];
line3 = Graphics[{Line[{{2.2, -3.8}, {2.9, -3.8}}]}];
arrow2a = Graphics[{Arrowheads[0.04], Arrow[{{0.7, -3.8}, {0, -3.8}}]}];
arrow2b = Graphics[{Arrowheads[0.04], Arrow[{{1.3, -3.8}, {1.98, -3.8}}]}];
text1 = Graphics[ Text[Style["L sin\[Theta]", FontSize -> 14, Purple], {1.0, -3.8}]];
text2 = Graphics[ Text[Style["mg", FontSize -> 14, Purple], {2.1, -4.8}]];
line3 = Graphics[{Line[{{1.0, -3.6}, {2.9, -3.6}}]}];
line4 = Graphics[{Line[{{2.2, -3.0}, {2.9, -3.0}}]}];
text3 = Graphics[ Text[Style["L(1 - cos\[Theta])", FontSize -> 14, Purple], {2.7, -3.3}]];
arrow3a = Graphics[{Arrowheads[0.04], Arrow[{{2.6, -3.35}, {2.6, -3.6}}]}];
arrow3b = Graphics[{Arrowheads[0.04], Arrow[{{2.6, -3.27}, {2.6, -3.0}}]}];
text4 = Graphics[ Text[Style["L", FontSize -> 14, Purple], {1.2, -1.5}]];
text5 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Purple], {0.1, -0.5}]];
text6 = Graphics[ Text[Style["O", FontSize -> 14, Purple], {-0.16, -0.2}]];
textT = Graphics[ Text[Style["T", FontSize -> 14, Black], {1.15, -2.1}]];
arrowT = Graphics[{Blue, Arrowheads[0.08], Arrow[{{1.88, -2.8}, {1.2, -1.8}}]}];
Show[top, circle1, circle2, circle3, line1, line2, line3, arrow, arrow2a, arrow2b,
text1, text2, line4, text3, arrow3a, arrow3b, text4, text5, text6, arrowT, textT]

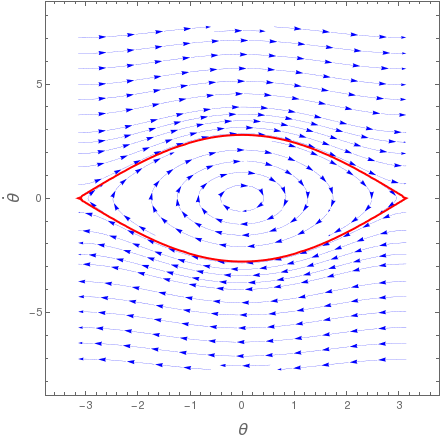
There are known two general approaches to derive the pendulum equation. The first one is based on Newton's second law (written for rotational motion):

\[ I_0 \frac{{\text d}^2 \theta}{{\text d} t^2} = \tau \qquad \mbox{or} \qquad I_0 \ddot{\theta} = \tau , \]
where I0 = m ℓ² is the moment of inertia for the bob of mass m, τ is the (magnitude of) torque acting on point mass (bob), and superdot is used to identify the derivative with respect to time variable t. The magnitude τ of the torque is the projection of weight mg on tangent line multiplied by the length ℓ (because the arc length equation is s = ℓθ):   τ = -mgℓsinθ. Therefore, we get the pendulum equation
\[ m\ell^2 \ddot{\theta} = -mg\ell\,\sin \theta \qquad \Longrightarrow \qquad \ddot{\theta} + \left( g/\ell \right) \sin \theta =0 . \qquad\blacktriangleleft \]
Manipulate[
Show[StreamPlot[{y, -9.81/l Sin[x]}, {x, - Pi, Pi}, {y, -7.5, 7.5}, FrameLabel -> {Style["\[Theta]", 16], Style["\!\(\*OverscriptBox[\(\[Theta]\), \(.\)]\)", 16]}, StreamPoints -> 50, StreamStyle -> {Blue, Thin}],
ContourPlot[ y^2/2 - 9.81/l Cos[x] == 9.81/l, {x, - Pi, Pi}, {y, -7.5, 7.5},
ContourStyle -> {Thick, Red}], ImageSize -> 1.1 {400, 400}], {{l, 4, "pendulum length"}, 1, 10, 0.1, Appearance -> "Labeled"}]
We can obtain the same differential equation using second Newton's law in rectangular coordinates (x, y):
\[ \begin{split} m\,\ddot{x} &= - T\,\sin \theta , \\ m\,\ddot{y} &= mg - T\,\cos \theta , \end{split} \]
where T is the tension in the rod, m is bob's mass, and g is the acceleration due to gravity. Since
\[ x = \ell\,\sin\theta \qquad\mbox{and}\qquad y = -\ell +\ell\,\cos\theta , \]
we have
\[ \ddot{x} = \ell \,\cos\theta\,\ddot{\theta} -\ell\,\sin\theta\,\dot{\theta}^2 , \qquad \ddot{y} = -\ell \,\sin\theta\,\ddot{\theta} - \ell\,\cos\theta\,\dot{\theta}^2 . \]
From the first equation \( m\,\ddot{x} = - T\,\sin \theta , \) we eliminate the tension to obtain \( \displaystyle T = - m\,\ddot{x} \,\frac{1}{\sin\theta} . \) Substituting this expression into the second equation, we get
\[ m\,\ddot{y} = mg - T\,\cos \theta = mg + m\,\ddot{x} \, \frac{\cos\theta}{\sin\theta} . \]
Eliminating common multiple m and using expressions for the second derivatives, we obtain
\[ \ddot{y} = -\ell \,\sin\theta\,\ddot{\theta} - \ell\,\cos\theta\,\dot{\theta}^2 = g + \frac{\cos\theta}{\sin\theta} \left[ \ell \,\cos\theta\,\ddot{\theta} -\ell\,\sin\theta\,\dot{\theta}^2 \right] . \]
Simplification of the above equation leads to the same pendulum equation.  ■

The second approach is based on the Euler--Lagrange equation (which we formulate for one degree of freedom, in our case):

\[ \frac{\text d}{{\text d}t} \,\frac{\partial {\cal L}}{\partial \dot{\theta}} = \frac{\partial {\cal L}}{\partial \theta} , \]
where \( {\cal L} = \mbox{K} - \Pi \) is the Lagrangian, which is the difference of the kinetic energy K and the potential energy Π of the system. We now compute the kinetic energy
\[ \mbox{K} = \frac{m}{2} \left( \dot{x}^2 + \dot{y}^2 \right) = \frac{m}{2}\, \ell^2 \left[ \left( -\dot{\theta} \,\sin \theta \right)^2 + \left( \dot{\theta} \,\cos\theta \right)^2 \right] = \frac{m}{2}\,\ell^2 \dot{\theta}^2 . \]
The kinetic and potential energies are

\[ \mbox{K} = \frac{1}{2}\, I_0 \dot{\theta}^2 , \qquad\mbox{and} \qquad \Pi = mgy = mg\ell \left( 1- \cos \theta \right) , \]
where \( I_0 = m\ell^2 \) is the moment of inertia of the pendulum. Calculating partial derivatives, we get
\[ \frac{\partial \mbox{K}}{\partial \dot{\theta}} = I_0 \dot{\theta} = m\ell^2 \dot{\theta} , \qquad \frac{\partial \Pi}{\partial \theta} = mgy = mg\ell \, \sin \theta . \]
Using these expressions, we obtain from the Euler--Lagrange equation \( \displaystyle \frac{\text d}{{\text d} t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}} \right) = \frac{\partial {\cal L}}{\partial \theta} , \) for the Lagrangian \( {\cal L} = \mbox{K} - \Pi , \) the pendulum equation in a vacuum:
\[ \ddot{\theta} + \left( g/\ell \right) \sin \theta =0 \qquad \mbox{or} \qquad \ddot{\theta} + \omega_0^2 \sin \theta =0 \qquad \left( \omega_0^2 = g/\ell \right) , \]
where \( \ddot{\theta} = {\text d}^2 \theta / {\text d}t^2 \) , \( \omega_0 = \sqrt{g/\ell} >0 ,\) and g is gravitational acceleration. For small oscillations (to have four decimal place accuracy, the angle θ needs to be less than 0.07 or about 4˚ in absolute value), we can replace sine function by its linear approximation, which leads to a linear differential equation
\[ \ddot{\theta} + \left( g/\ell \right) \theta =0 \qquad \Longleftrightarrow \qquad \ddot{\theta} + \omega_0^2 \theta =0 \qquad \left( \omega_0^2 = g/\ell \right) . \]
We assume that the oscillations of the pendulum are subjected to the initial conditions \( \theta(0) = \theta_0 , \qquad \dot{\theta}(0) = v_0, \) where θ0 is the initial amplitude of the oscillation and v0 is its initial velocity. The system oscillates between symmetric limits \( [- \theta_{\max} , \theta_{\max} ] . \) Here \( \theta_{\max} \) is the maximum displacement of the bob from its vertical position that could be defined as the angle when the velocity is zero: \( \dot{\theta} = 0. \) The periodic motion exhibited by a simple pendulum is harmonic only for small angle oscillations. Beyond this limit, the equation of motion is nonlinear: the simple harmonic motion is unsatisfactory to model the pendulum motion for large amplitudes and in such cases the period depends on amplitude. The periodic solution \( \theta (t) \) and the angular frequency ω (also with the period \( T = 2\pi /\omega \) ) depends on the initial amplitude θ(0) and the initial velocity \( \dot{\theta} (0) . \)  ◄

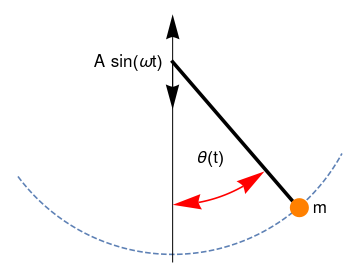
Example: Consider a simple pendulum problem when its pivot is undergoing vertical oscillations given by A sin(ωt) as shown. To solve this parametric excitation problem, the rectangular coordinates of the mass m are first expressed in terms of the length ℓ and angle θ(t), t being time.

a = {Graphics[{Arrowheads[{-0.07, 0.07}], Arrow[{{0, -0.5}, {0, 0.5}}]}]};
dash = ParametricPlot[{2.02*Cos[t], 2.02*Sin[t]}, {t, -2.5, -0.5}, PlotStyle -> Dashed, Axes -> False];
vline = Graphics[Line[{{0, 0}, {0, -2.1}}]];
angle = ParametricPlot[#[[1]]*{Cos[\[Theta]], Sin[\[Theta]]}, {\[Theta], #[[2]], #[[3]]}, Axes -> False, PlotStyle -> #[[4]]] /. Line[x_] :> Sequence[Arrowheads[{-0.08, 0.08}], Arrow[x]] & /@ {{-1.5, 90 Degree, 130 Degree, Red}};
line = Graphics[{Thickness[0.01], Line[{{0, 0}, {1.25, -1.45}}]}];
disk = Graphics[{Orange, Disk[{1.33, -1.53}, 0.1]}];
sin = Graphics[ Text[Style["A sin(\[Omega]t)", FontSize -> 16, Black], {-0.46, 0.0}]];
theta = Graphics[ Text[Style["\[Theta](t)", FontSize -> 16, Black], {0.4, -1.0}]];
m = Graphics[Text[Style["m", FontSize -> 16, Black], {1.55, -1.53}]];
Show[dash, a, vline, angle, line, disk, sin, m, theta, PlotRange -> All]
\[ \begin{split} x&= \ell\,\sin \left( \theta (t) \right) , \\ y&= \ell \left( 1 - \cos \theta (t) \right) + A\,\sin (\omega t) . \end{split} \]
The x and y velocity components are calculated as
\[ \begin{split} \dot{x}&= v_1 = \ell\,\cos \left( \theta (t) \right) \frac{\partial \theta}{\partial t} , \\ \dot{y}&= v_2 = \ell \,\sin \theta (t) \,\frac{\partial \theta}{\partial t} + A\,\cos (\omega t) \,\omega . \end{split} \]
The kinetic energy is calculated as usual:
\[ \mbox{K} = \frac{m}{2} \left( \dot{x}^2 + \dot{y}^2 \right) = \frac{m}{2} \left[ \ell^2 \cos \theta \left( \frac{\partial \theta}{\partial t} \right)^2 + \left( \ell\,\sin \theta \,\dot{\theta} + A\,\cos (\omega t)\,\omega \right)^2 \right] . \]
With the aid of Simplify command, we get
\[ \mbox{K} = \frac{m}{2} \,\ell^2 \dot{\theta}^2 + m\ell\,\omega \,\sin \theta \,\dot{\theta}\,A\,\cos (\omega t) + \frac{m}{2} \,A^2 \cos^2 (\omega t) \,\omega^2 . \]
The potential energy becomes
\[ \Pi = mg\,y = mg\ell \left( 1 - \cos \theta \right) + A\,\sin (\omega t) . \]
Then we form the Lagrangian as the difference of the kinetic energy and the potential energy, which leads to the differential equation of motion:
\[ \ddot{\theta} + \frac{1}{\ell} \left[ g - A\,\omega^2 \sin )\omega t) \right] \sin \theta = 0 . \]
   ■

Example: Consider a pendulum excited both at a slow and a high frequency. The motion of the pendulum is governed by the following equation: ̈

\[ \ddot{\theta} + 2\beta\,\dot{\theta} + \sin\theta = - \ddot{u}\,\sin\theta - \ddot{v}\,\cos \theta , \]
where
\[ u(t) = a_v (t) + a_v (t)\, \sin \omega t , \qquad u(t) = a_h (t) + a_v (t)\,\sin \omega t , \qquad \omega \gg 1. \]
   ■

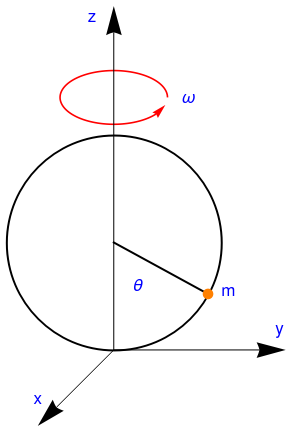
Example: A vertically oriented circular wire of radius ℓ rotates with angular velocity ω about the z-axis. A bead of unit mass (m = 1) is allowed to slide along the frictionless wire.

arc = Show[ ParametricPlot[#[[1]]*{Cos[\[Theta]]*0.5 - 1.35, 0.25 Sin[\[Theta]]} + 1.35, {\[Theta], #[[2]], #[[3]]}, Axes -> False, PlotStyle -> #[[4]]] /. Line[x_] :> Sequence[Arrowheads[{0, 0.05}], Arrow[x]] & /@ {{1, 0 , 6, Red}}, PlotRange -> All]
circle = Graphics[{Thick, Circle[{0, 0}, 1]}]
arrowx = Graphics[{Arrowheads[0.1], Arrow[{{0, -1}, {-0.707, -1.707}}]}]
arrowy = Graphics[{Arrowheads[0.1], Arrow[{{0, -1}, {1.6, -1}}]}]
arrowz = Graphics[{Arrowheads[0.1], Arrow[{{0, -1}, {0, 2.2}}]}]
line = Graphics[{Thick, Line[{{0, 0}, {0.877, -0.479}}]}]
disk = Graphics[{Orange, Disk[{0.877, -0.479}, 0.05]}]
txtx = Graphics[Text[Style["x", FontSize -> 16, Blue], {-0.7, -1.45}]]
txty = Graphics[Text[Style["y", FontSize -> 16, Blue], {1.55, -0.8}]]
txtz = Graphics[Text[Style["z", FontSize -> 16, Blue], {-0.2, 2.1}]]
txto = Graphics[ Text[Style["\[Omega]", FontSize -> 16, Blue], {0.7, 1.35}]]
txtt = Graphics[ Text[Style["\[Theta]", FontSize -> 16, Blue], {0.23, -0.4}]]
txtm = Graphics[Text[Style["m", FontSize -> 16, Blue], {1.07, -0.45}]]
Show[circle, arc, arrowx, arrowy, arrowz, line, disk, txtx, txty, \ txtz, txto, txtt, txtm]
Using the Lagrangian, we find
\[ \ddot{\theta} + \omega_0^2 \sin\theta - \frac{\omega^2}{2}\,\sin (2\theta ) = 0 . \]
We plot solutions and then plot angle versus its velocity.
ssol = NDSolve[{y''[t] + Sin[y[t]] - 0.5*Sin[2*y[t]] == 0, y[0] == 1, y'[0] == -0.2}, y, {t, 0, 100}, AccuracyGoal -> 10, PrecisionGoal -> 10]
Plot[Evaluate[y[t] /. ssol], {t, 0, 20}, PlotPoints -> 1000, Frame -> True, PlotStyle -> {Thick, Hue[0.9]}, FrameLabel -> {"time", "angle"}, ImageSize -> {600, 400}, LabelStyle -> {FontFamily -> "Times", FontSize -> 16}]
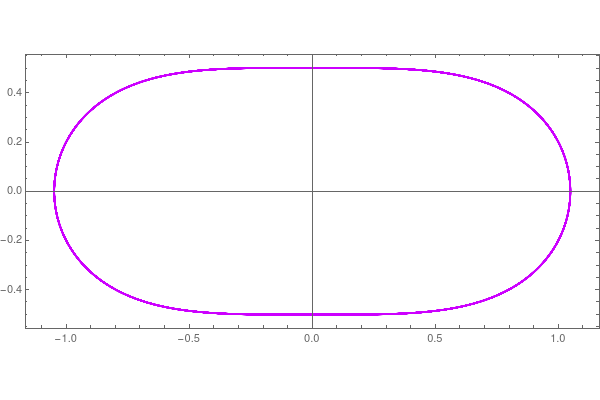
ParametricPlot[ Evaluate[{y[t], y'[t]} /. ssol, {t, 0, 100}, Frame -> True, PlotStyle -> Hue[0.8], ImageSize -> {600, 400}]]
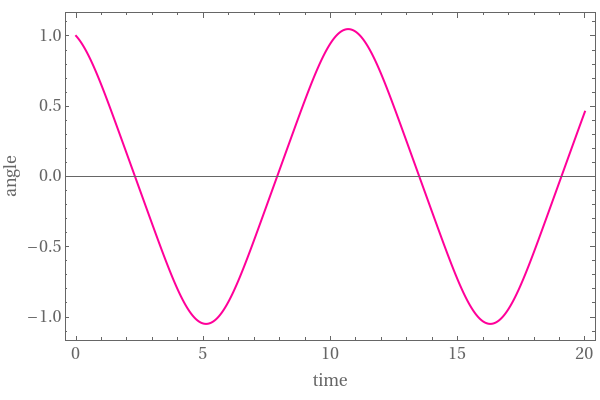Graph of angle vs time Graph of angle vs velocity
   ■

 

  1. Scientific Computing by Jeffrey R. Chasnov.
  2. Fidlin, A., Bi-harmonically excited pendulum: shifted resonances and quenching the low frequency excitation, 2006, PAMM Proc Appl Math Mech , Volume 6, pp. 301--302. doi: 10.1002/pamm.200610132
  3. Fidlin, A., Nonlinear Oscillations in Mechanical Engineering, 2006, Springer-Verlag, Berlin, New York.
  4. Ganji, D.D., Karimpour, S., and Ganji, S.S., Approximate analytical solutions to nonlinear oscilations of non-natural systems using He's energy balance method, Progress in Electromagnetics Research, 2008, Vol. 5, pp. 43--54.

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)