Preface

This section demonstrates an application of the power series method in solving first order differential equations.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part V of the course APMA0330

Glossary

Examples for first order ODEs solved by Power Series

We believe that the best way to learn a material and techniques is go by examples. Therefore, this section contains a detail exposition of several examples.

 

Example: Consider the initial value problem

\[ \frac{{\text d}y(t)}{{\text d}t} = 1\, y(t) -y^2 (t) , \qquad y(0) =1. \]
Its solution is
\[ y(t) = \frac{e^t}{\cosh t} = 1+t - \frac{t^3}{3} + \frac{2}{15}\, t^5 - \frac{17}{315}\, t^7 + \frac{62}{2835}\, t^9 - \frac{1382}{155 925}\, t^{11} + \cdots . \]
Although these formulas were found with the aid of a computer algebra system, we are going to rederive the power series for its solution \( y = \sum_{n\ge 0} c_n t^n . \) For the slope function f(y) = 2y - y², we find
\[ c_0 = y(0) =1 \qquad \mbox{and} \qquad c_1 = y' (0) = f(1) = 1 . \]
   ■

 

Example: Consider the initial value problem

\[ \frac{{\text d}y(x)}{{\text d}x} = \frac{y^2 (x)}{4 - x\,y} , \qquad y(0) =1. \]
Its solution exists in the interval (-∞, 4/e) ≈ (-∞, 1.47152) because it is the implicit solution of the equation \( y = e^{xy/4} , \) which is expressed through the Lambert function. We first try to solve the IVP with Mathematica
Simplify[DSolve[{y'[x] == (y[x])^2/(4 - x*y[x]), y[0] == 1}, y[x], x]]
{{y[x] -> -((4 ProductLog[-(1/4) (x^4)^(1/4)])/x)}}
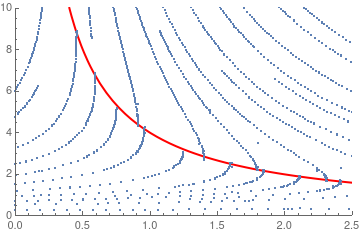
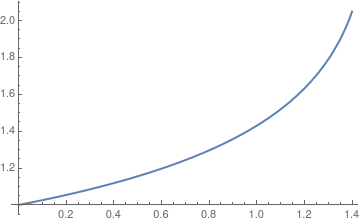
where ProductLog is another name for Lambert function. Then we plot its solution using standard Mathematica command NDSolve and display the corresponding stream plot along with the singular line (in red) y = 4/x.
sol = NDSolve[{y'[x] == (y[x])^2/(4 - x*y[x]), y[0] == 1}, y, {x, 0, 1.47}]
Plot[y[x] /. sol, {x, 0, 1.4}, PlotStyle -> Thick]
stream = ListPlot[ Reap[StreamPlot[{1, y^2/(4 - x*y)}, {x, 0, 2.5}, {y, 0, 10}, EvaluationMonitor :> Sow[{x, y}]]][[-1, 1]]]
hyper = Plot[4/x, {x, 0.3, 2.6}, PlotStyle -> {Thick, Red}, PlotRange -> {{0, 2.5}, {0, 10}}]
Show[hyper, stream]
         Stream plot       Solution curve

The given differential equation has a moving singularity: y = 4/x, indicated on the graph by red curve. Now we seek its solution in power series form:

\[ y(x) = c_0 + \sum_{n\ge 1} c_n x^n , \qquad \mbox{where } c_0 =1. \]
The next coefficient in the above Taylor's series is also not hard to evaluate:
\[ c_1 = y' (0) = f(0,1) = \left. \frac{y^2}{4 - x\,y} \right\vert_{x=0, y=1} = \frac{1}{4} . \]
The second coefficient requires differentiation:
\[ c_2 = \frac{1}{2!} \,y'' (0) = \frac{1}{2} \, \left. \frac{text d}{{text d}x} \,\frac{y^2}{4 - x\,y} \right\vert_{x=0, y=1} = \left. \frac{2y^3 \left( xy-6 \right)}{\left( 4 - xy \right)^3} \right\vert_{x=0, y=1} = \frac{3}{2} \]
because Mathematica does all calculations
f[x_, y_] = y^2 /(4 - x*y); D[f[x, y[x]], x] % /. y'[x] -> f[x, y] Simplify[(2 y* y^2 /(4 - x*y))/(4 - x y) - ( y^2 (-y - x y^2 /(4 - x*y)))/(4 - x y)^2]
(2 y^3 (-6 + x y))/(-4 + x y)^3
   ■

 

Example: Consider the initial value problem

\[ \frac{{\text d}y}{{\text d}x} = g(x) + e^{-y(x)} , \qquad y(x_0 ) = 0, \]
where g is a continuous function defined on an (open) interval, including the initial point x0.    ■

 

 

  1. Duan, J.-S. and Rach, R., The degenerate form of the Adomian polynomials in the power series method for nonlinear ordinary differential equations, Journal of Mathematics and System Science, Volume 5, Pages 411--428, doi: 10.17265/2159-5291/2015.10.003

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)