Preface

This section discusses differential equation used to model vibration of springs,

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part IV of the course APMA0330

Glossary

Spring Problems

Sometimes it is necessary to consider the second derivative when constructing a mathematical model. There are known two famous areas of applications: mechanical and electrical oscillations. For example, the motion of a mass on a vibrating spring, the torsional oscillations of a shaft with a flywheel, the flow of electric current in a simple series circuit, and many other physical problems are all described by the solution of an initial value problem of the form

\[ a\, \ddot{x} + b\,\dot{x} + c\,x = f(t), \qquad x(0) = x_0 , \quad \dot{x}(0) = v_0 . \]
Now we consider in detail two mechanical problems involving spring oscillations: horizontal and vertical. As it is often happen, both problems have the same mathematical model. We start with the vertical oscillations.

Vertical spring oscillations

A spring is an object that can be deformed by a force and then return to its original shape after the force is removed. Springs come in a huge variety of different forms, but what they all share is the elasticity. This term represents the reaction of a spring (or any other object) on axial load. When a force is placed on a material, the material stretches or compresses in response to the force. When the force is removed, the matrial returns to its original form.

When studying springs and elastic deformations, the 17ᵗʰ century British physicist Robert Hooke noticed that the stress vs strain curve for many materials has a linear region. Such proportionally of the extension of the spring to the applied force is known now as Hooke's law. Robert Hooke (1635--1703) was a scientist with wide-ranging interests. He published the book Micrographia in 1665 where he first formulated the law named after him.

Consider a mass m hanging at rest on the end of a vertical spring of original length \( \ell . \) The mass causes an elongation L of the spring in the downward direction, which we assume positive. In this static situation there are two forced acting at the point where the mass is attached to the spring. The gravitational force, or weight of the mass, acts downward and has magnitude mg, where g is the acceleration due to gravity. There is also a force, which we denote as F, due to the spring that acts upward. If we assume that the elongation L of the spring is small, the spring force is very nearly proportional to L: \( F = -k\,L , \) where k is called the spring constant. Since the mass is in equilibruim, the two forces balance each other, which means that

\[ mg - k\,L =0 \qquad \Longrightarrow \qquad mg = k\,L . \]
This mass m is pushed into the motion either by an external force or by initial displacement or by both. Let x(t), measured positive downward, denote the displacement of the mass from its equilibrium position at time t. Then x(t) is related to the forces acting on the mass through Newton's law of motion
\[ m\,\ddot{x} (t) = f(t) , \]
where \( \ddot{x} \) is the accelation of the mass and f is the net force acting on the mass. Observe that there are now four separate forces to be considered: Taking into account all these forces, we obtain the following equation of motion:
\begin{align*} m\,\ddot{x} (t) &= mg + F_s (t) + F_r (t) + F(t) \\ &= mg - k\left( L + x (t) \right] - \gamma \,\dot{x} = F(t) \end{align*}
Since mg = kL , the above equation is simplified to
\[ m\,\ddot{x} + \gamma \dot{x} + k\,x(t) = F(t) , \]
where constants m, γ, and k are positive.

Horizontal spring oscillations

Suppose that we have a mass lying on a flat, frictionless surface and that this mass is attached to one end of a spring with the other end of the spring attached to a wall. We denote the spring displacement by x. If x>0, then the spring is stretched. If x<0, the spring is compressed. If x = 0, then the spring is in a state of equilibrium. If we pull on the mass, then the mass will oscillate back and forth across the table.

spring1 = ParametricPlot[{t + Cos[3*t], 2*Sin[3*t]}, {t, 0, 4*Pi}]
wall = Graphics[{Pink, Polygon[{{-5, -5}, {-5, 5}, {-3, 5}, {-3, -5}}]}]
line1 = Graphics[Line[{{-3, 0}, {1, 0}}]]
line2 = Graphics[Line[{{4*Pi + 1, 0}, {20, 0}}]]
box = Graphics[{LightBlue, Polygon[{{20, -2.5}, {20, 2.5}, {25, 2.5}, {25, -2.5}}]}]
ground = Graphics[ Polygon[{{17, -2.5}, {26, -2.5}, {26, -3.5}, {17, -3.5}}]]
Show[box, line1, line2, wall, spring1, ground]
We can construct a differential equation that models our oscillating mass. First, we must consider the restorative force on the spring. We will make the assumption that this force depends on the displacement of the spring, F(x). Using Taylor's Theorem from calculus, we can expand F to obtain
\begin{align*} F(x) &= F(0) + F' (0) \,x + \frac{1}{2}\,x^2 F''(0) + \cdots \\ &= -k\,x + \frac{1}{2}\,x^2 F''(0) + \cdots , \end{align*}
where \( F' (0) =-k \) and F(0) = 0. If the displacement is not too large, then xn will be small for \( n \ge 2, \) and we can ignore higher ordered terms. Thus, we can consider the restorative force on the spring to be proportional to displacement of the spring from its equilibrium length,
\[ F(x) \approx - k\,x . \]
This equation is known as is Hooke's Law. We can test this law experimentally, and it is reasonably accurate if the displacement of the spring, x, is not too large.

By Newton's second law of motion, the force on the mass m must be

\[ F(x) = m\, \ddot{x} . \]
Setting the two forces equal, we have a second order differential equation,
\[ m\, \ddot{x} = -k\, x \qquad\mbox{or} \qquad \ddot{x} + \omega^2 x =0 , \]
where \( \omega^2 = k/m , \) which describes our oscillating mass. The spring-mass system is an example of a harmonic oscillator.

Now let us add a damping force to our system. For example, we might add a dashpot, a mechanical device that resists motion, to our system. Think of a dashpot as the small cylinder that keeps your screen door from slamming shut. The simplest assumption would be to take the damping force of the dashpot to be proportional to the velocity of the mass, \( \dot{x}(t) . \) Thus, we have will have an additional force, \( F(x) = -b\,\dot{x}(t) , \) acting on our mass, where b > 0. Our new equation for the spring-mass system is

\[ m\,\ddot{x} + b\,\dot{x} + k\, x =0 . \]

Consider a linear damped oscillator:
\[ m\,\ddot{x} + b\,\dot{x} + k\, x =0 ,\qquad \mbox{with initial conditions: } x(0) = x_0 , \ \dot{x}(0) = v_0 , \]
for some positive parameters m, b, and k. It is convenient to transfer the given differential equation to a system by introducing the velocity variable \( v= \dot{x} . \) The result is
\[ v= \dot{x} , \quad \dot{v} = - \frac{b}{m}\,v - \frac{k}{m}\, x , \qquad \mbox{subject to } x(0) = x_0 , \ v(0) = v_0 . \]
We define the equation for Mathematica:
osc[m_, b_, k_, x0_, v0_] :=
{x'[t] == v[t], v'[t] == -(b / m) * v[t] - (k / m) * x[t], x[0] == x0, v[0] == v0}
We define a routine which gives the result of integrating the differential equation with NDSolve, starting at t = 0, and integrating out to t = tfinal.

1.4.9. Applications

Example 4.9.2: Pure oscillations give the solutions of the following differential equation subject to the given initial conditions (displacement is 1, but velocity is zero):

\[ \ddot{x} (t) + 25\,x(t) =0 , \qquad x(0) =1, \quad \dot{x}(0) =0. \]

Clear[x,y,t,z];
soln = DSolve[{x''[t] + 25 x[t] == 0, x[0] == 1, x'[0] == 0}, x[t], t]
Plot[x[t] /. soln, {t, -1, 2.5}]
s[t_] = x[t]/.soln[[1]]
Plot[s[t],{t,0,3},AxesLabel->{"t","Displacement"}]

Example 4.9.3: Consider the initial value problem

\[ \ddot{x} + 17\,\dot{x} + 16\,x(t) =0, \qquad x(0) =1, \quad \dot{x} (0) =5. \]
soln = DSolve[{x''[t] + 17 x'[t] + 16 x[t] == 0, x[0] == 1, x'[0] == 5}, x[t], t];
s1[t_] = x[t] /. soln[[1]]
Out[32]= 1/5 E^(-16 t) (-2 + 7 E^(15 t))
Plot[s1[t], {t, 0, 3}, AxesLabel -> {"t", "Displacement"}]

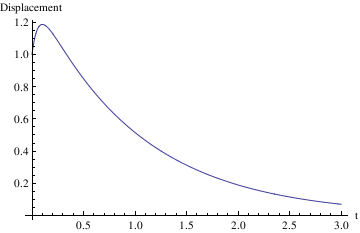
When does the maximum excursion occur?

FindRoot[s1'[t] == 0, {t, 0}]
Out[9]= {t -> 0.101322}
What is the maximum excursion?
s1[t /. %]
Out[10]= 1.18603

Example 4.9.4: Now we turn to a differential equation whose characteristic polynomial has a double root:

\[ \ddot{x} + 6\,\dot{x} + 9\,x =0, \qquad x(0) =-1, \quad \dot{x}(0) =5. \]

soln = DSolve[{x''[t] + 6 x'[t] + 9 x[t] == 0, x[0] == -1, x'[0] == 5}, x[t], t]
s2[t_] = x[t] /. soln[[1]]
Plot[s2[t], {t, 0.2, 3}, PlotStyle->{Thick,Magenta}]

Out[11]= {{x[t] -> E^(-3 t) (-1 + 2 t)}}
Out[12]= E^(-3 t) (-1 + 2 t)
Out[13]=

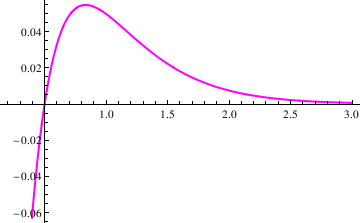
When does the extreme occur?
Solve[s2'[t] == 0, t]
out[48]= {{t -> 5/6}}
Where is the extreme?
s2[t /. %]
out[49]= {2/(3 E^(5/2))}
N[%]
out[50]= {0.0547233}

Example 4.9.5: We consider another initial value problem

\[ \ddot{x} + 2\,\dot{x} + 37\,x =0, \qquad x(0) =-1, \quad \dot{x} (0) =5. \]
Since the characteristic polynomial has complex roots \( \lambda = -1 \pm 6{\bf j} ,\) the solutions decay with oscillations.
soln = DSolve[{x''[t] + 2 x'[t] + 37 x[t] == 0, x[0] == -1,
x'[0] == 5}, x[t], t]
Out[2]= -(1/3) E^-t (3 Cos[6 t] - 2 Sin[6 t])}}
s3[t_] = x[t] /. soln[[1]]

Clear[x,t];
soln = DSolve[{x''[t] + 2 x'[t] + 37 x[t] == 0, x[0] == -1, x'[0] == 5}, x[t], t]
s3[t_] = x[t] /. soln[[1]]
Plot[s3[t], {t, 0, 3}, PlotRange -> {-1, 1}]

Out[19]= {{x[t] -> -(1/3) E^-t (3 Cos[6 t] - 2 Sin[6 t])}}
Out[20]= -(1/3) E^-t (3 Cos[6 t] - 2 Sin[6 t])
Out[21]=

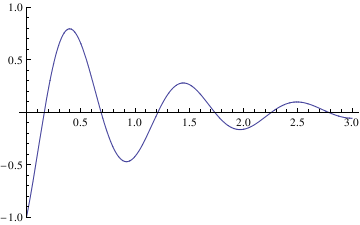
Now we define the amplitude of these oscillations:
amplitude = s3[t] /. c3_ Exp[c4_] (c1_ Cos[a_] + c2_ Sin[a_]) -> c3*Sqrt[c1^2 + c2^2]
Out[19]= -(Sqrt[13]/3)
Plot[{amplitude*Exp[-t], -amplitude*Exp[-t], s3[t]}, {t, 0, 3}, PlotStyle -> {Blue, Blue, Black}]

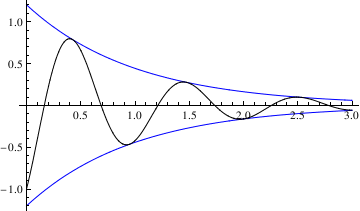
Example 4.9.6: Forced oscillations are modeled by the following nonhomogeneous equation:

\[ \ddot{x} + 10\,\dot{x} + 41\,x =25\,\sin 4t, \qquad x(0) =-1, \quad \dot{x}(0) =5. \]

soln = DSolve[{x''[t] + 10 x'[t] + 41 x[t] == 25 Sin[4 t], x[0] == -1, x'[0] == 5}, x[t], t]
Out[1]= {{x[t] ->
1/712 E^(-5 t) (-392 Cos[4 t] - 445 E^(5 t) Cos[4 t] +
125 E^(5 t) Cos[4 t] Cos[8 t] + 200 Sin[4 t] -
200 E^(5 t) Cos[8 t] Sin[4 t] + 200 E^(5 t) Cos[4 t] Sin[8 t] +
125 E^(5 t) Sin[4 t] Sin[8 t])}}

We extract the transient solution and the steady-state solution. First, we define the solution function:

ss[t_] = x[t] /. soln[[1]]
Out[2]= 5/712 E^(-5 t) (64 Cos[4 t] - 89 E^(5 t) Cos[4 t] + 25 E^(5 t) Cos[4 t] Cos[8 t] + 40 Sin[4 t] -
40 E^(5 t) Cos[8 t] Sin[4 t] + 40 E^(5 t) Cos[4 t] Sin[8 t] + 25 E^(5 t) Sin[4 t] Sin[8 t])
Then we find the steady-state solution by finding the general solution of the given differential equation
gensol = DSolve[{x''[t] + 10 x'[t] + 41 x[t] == 25 Sin[4 t]}, x[t], t]
Out[3]= {{x[t] -> E^(-5 t) C[2] Cos[4 t] + E^(-5 t) C[1] Sin[4 t] - 5/712 (89 Cos[4 t] - 25 Cos[4 t] Cos[8 t] +
40 Cos[8 t] Sin[4 t] - 40 Cos[4 t] Sin[8 t] - 25 Sin[4 t] Sin[8 t])}}
gs[t_] = x[t] /. gensol[[1]]
Out[4]= E^(-5 t) C[2] Cos[4 t] + E^(-5 t) C[1] Sin[4 t] - 5/712 (89 Cos[4 t] - 25 Cos[4 t] Cos[8 t] +
40 Cos[8 t] Sin[4 t] - 40 Cos[4 t] Sin[8 t] - 25 Sin[4 t] Sin[8 t])
and then vanishing arbitrary constants:
steadyState[t_] = gs[t] /. {C[1] -> 0, C[2] -> 0}
Out[5]= -(5/712) (89 Cos[4 t] - 25 Cos[4 t] Cos[8 t] + 40 Cos[8 t] Sin[4 t] - 40 Cos[4 t] Sin[8 t] - 25 Sin[4 t] Sin[8 t])
Then the transient solution will be their difference:
transient[t_] = Simplify[ss[t] - steadyState[t]]
Out[6]= 1/89 E^(-5 t) (-49 Cos[4 t] + 25 Sin[4 t])
Then we check the initial conditions:
steadyState[0]
Out[7]= -(40/89)
D[steadyState[t], t] /. t -> 0
Out[8]= 100/89
transient[0]
Out[9]= -(49/89)
D[transient[t], t] /. t -> 0
Out[10]= 345/89
ss[0]
Out[11]= -1
D[ss[t], t] /. t -> 0
Out[12]= 5

Now we consider a similar problem but with another input function:

Clear[soln,L,x]
L[t_,x_] = x''[t] + 10 x'[t] + 41 x[t];
solnRule = DSolve[{L[t, x] == 8 *Exp[-5*t] Cos[2 t], x[0] == -1, x'[0] == 5}, x[t], t]
Out[3]= {{x[t] ->
1/6 E^(-5 t) (-13 Cos[4 t] + 6 Cos[t]^2 Cos[4 t] +
Cos[4 t] Cos[6 t] + 3 Sin[2 t] Sin[4 t] + Sin[4 t] Sin[6 t])}}
s[t_] = x[t] /. solnRule[[1]]
Out[4]= 1/6 E^(-5 t) (-13 Cos[4 t] + 6 Cos[t]^2 Cos[4 t] +
Cos[4 t] Cos[6 t] + 3 Sin[2 t] Sin[4 t] + Sin[4 t] Sin[6 t])
Then we find the general solution
gensol = DSolve[{x''[t] + 10 x'[t] + 41 x[t] == 8*Exp[-5*t] Cos[2 t]}, x[t], t]
Out[5]= {{x[t] ->
E^(-5 t) C[2] Cos[4 t] + E^(-5 t) C[1] Sin[4 t] +
1/6 E^(-5 t) (6 Cos[t]^2 Cos[4 t] + Cos[4 t] Cos[6 t] +
3 Sin[2 t] Sin[4 t] + Sin[4 t] Sin[6 t])}}
gs[t_] = x[t] /. gensol[[1]]
Out[6]= E^(-5 t) C[2] Cos[4 t] + E^(-5 t) C[1] Sin[4 t] +
1/6 E^(-5 t) (6 Cos[t]^2 Cos[4 t] + Cos[4 t] Cos[6 t] +
3 Sin[2 t] Sin[4 t] + Sin[4 t] Sin[6 t])
Now the steady-state solution is
steadyState[t_] = gs[t] /. {C[1] -> 0, C[2] -> 0}
Out[6]= 1/6 E^(-5 t) (6 Cos[t]^2 Cos[4 t] + Cos[4 t] Cos[6 t] + 3 Sin[2 t] Sin[4 t] + Sin[4 t] Sin[6 t])

and the transient solution becomes

transient[t_] = Simplify[s[t] - steadyState[t]]
Out[7]= -(13/6) E^(-5 t) Cos[4 t]
Now we plot two transient solutions:
Plot[{1/89 E^(-5 t) (-49 Cos[4 t] + 25 Sin[4 t]) , transient[t]},{t,0,3}, PlotStyle->{Thick,{Blue,Pink}}]

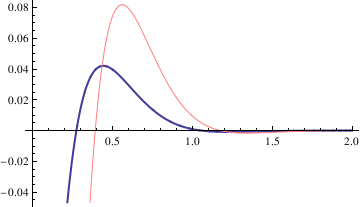
We also plot two solutions

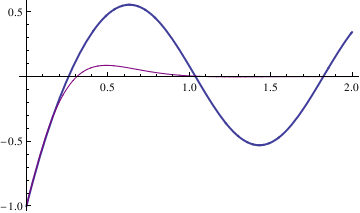
Plot[{ss[t], s[t]}, {t, 0, 2}, PlotStyle -> {Thick, {Cyan, Purple}}]

Transient solutions could be plotted in a similar way.

Plot[x[t] - steadyState[t], {t, 0, 1.5}, PlotRange -> {-1/2, 0.2}]

Example 4.9.7: Undamped Spring with External Forcing.

Enter the coefficients and the differential equation:

F0 = 1; omega = 2; k = 5;
ode = y''[t] + k^2*y[t] == F0*Cos[omega*t];
Solve the initial value problem:
DSolve[{ode, y[0] == 0, y'[0] == 0}, y[t], t]
Out[3]= {{y[t] ->
1/210 (-10 Cos[5 t] + 7 Cos[3 t] Cos[5 t] + 3 Cos[5 t] Cos[7 t] +
7 Sin[3 t] Sin[5 t] + 3 Sin[5 t] Sin[7 t])}}
Copy the output from the preceding step to define the solution function soln[t]:
soln[t_] = y[t] /. %[[1]]
Out[4]= 1/210 (-10 Cos[5 t] + 7 Cos[3 t] Cos[5 t] + 3 Cos[5 t] Cos[7 t] +
7 Sin[3 t] Sin[5 t] + 3 Sin[5 t] Sin[7 t])
Plot the solution function.
Plot[soln[t], {t, 0, 10}, AxesLabel -> {"t", "y[t]"}, PlotStyle->{Thick,Pink}]
Define the derivative function as v[t], and plot the trajectory in the phase plane. (You may need to enlarge the plot to see details.)

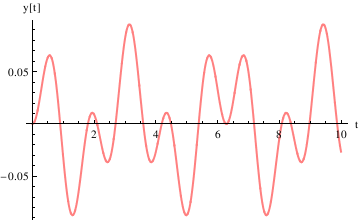
Example 4.9.8: Beats

We reconsider Example 1.4.7 for periodic input, when resonance is observed.
Enter the coefficients and the differential equation.

F0 = 1; omega = 4; k = 5;
ode = y''[t] + k^2*y[t] == F0*Cos[omega*t];
Solve the initial value problem:
DSolve[{ode, y[0] == 0, y'[0] == 0}, y[t], t]
Out[3]= {{y[t] ->
1/90 (-10 Cos[5 t] + 9 Cos[t] Cos[5 t] + Cos[5 t] Cos[9 t] +
9 Sin[t] Sin[5 t] + Sin[5 t] Sin[9 t])}}
Copy the output from the preceding step to define the solution function y[t]:

y[t_] = y[t] /. %[[1]]
Out[4]= 1/90 (-10 Cos[5 t] + 9 Cos[t] Cos[5 t] + Cos[5 t] Cos[9 t] +
9 Sin[t] Sin[5 t] + Sin[5 t] Sin[9 t])
Plot the solution function:
Plot[y[t], {t, 0, 15}, AxesLabel -> {"t", "y[t]"}, PlotStyle->{Thick,Green}]

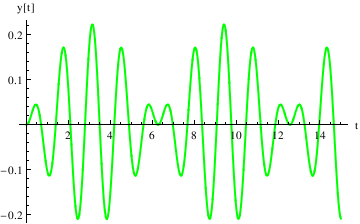
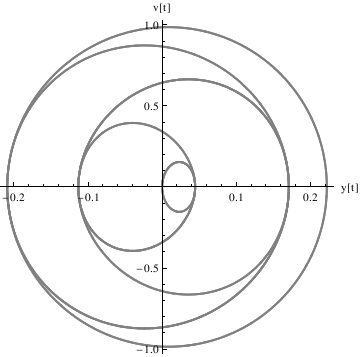
Define the derivative function as v[t], and plot the trajectory in the phase plane:

v[t_] = D[y[t], t]
Out[6]= 1/90 (36 Cos[5 t] Sin[t] + 50 Sin[5 t] - 36 Cos[t] Sin[5 t] +
4 Cos[9 t] Sin[5 t] - 4 Cos[5 t] Sin[9 t])
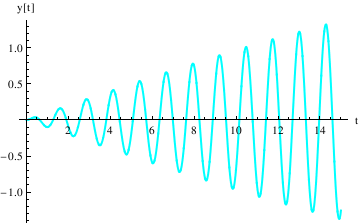
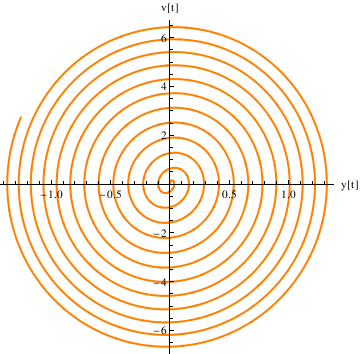
ParametricPlot[{y[t], v[t]}, {t, 0, 15}, AspectRatio -> 1, AxesLabel -> {"y[t]", "v[t]"}, PlotStyle->{Thick,Gray}]

Example 4.9.9: Resonance

We repeat the commands (after quitting the kernel) here for defining the coefficients and the differential equation---now with \[omega] very close to k:

F0 = 1; omega = 4.9; k = 5;
ode = y''[t] + k^2*y[t] == F0*Cos[omega*t];
DSolve[{ode, y[0] == 0, y'[0] == 0}, y[t], t]
Out[3]= {{y[t] ->-1.0101 Cos[5. t] + 1. Cos[0.1 t] Cos[5. t] +
0.010101 Cos[5. t] Cos[9.9 t] + 1. Sin[0.1 t] Sin[5. t] +
0.010101 Sin[5. t] Sin[9.9 t] }}
y[t_] = y[t] /. %[[1]]
Out[4]= -1.0101 Cos[5. t] + 1.0101 Cos[4.9 t] Cos[5. t]^2 +
1.0101 Cos[4.9 t] Sin[5. t]^2
Plot[y[t], {t, 0, 15}, AxesLabel -> {"t", "y[t]"}, PlotStyle->{Thick,Cyan}]
Now we find the velocity
v[t_] = D[y[t], t]
Out[6]= 0. - 4.94949 Cos[5. t]^2 Sin[4.9 t] + 5.05051 Sin[5. t] -
4.94949 Sin[4.9 t] Sin[5. t]^2
and plot v versus y:
ParametricPlot[{y[t], v[t]}, {t, 0, 15}, AspectRatio -> 1, AxesLabel -> {"y[t]", "v[t]"}, PlotStyle->{Thick,Orange}]

F0 = 1; omega = 2; k = 5;
ode = y''[t] + k^2*y[t] == F0*Cos[omega*t];
DSolve[{ode, y[0] == 0, y'[0] == 0}, y[t], t]
y[t_] = y[t] /. %[[1]]
Out[3]= {{y[t] ->
1/210 (-10 Cos[5 t] + 7 Cos[3 t] Cos[5 t] + 3 Cos[5 t] Cos[7 t] +
7 Sin[3 t] Sin[5 t] + 3 Sin[5 t] Sin[7 t])}}
Out[4]= 1/210 (-10 Cos[5 t] + 7 Cos[3 t] Cos[5 t] + 3 Cos[5 t] Cos[7 t] +
7 Sin[3 t] Sin[5 t] + 3 Sin[5 t] Sin[7 t])
Plot[y[t], {t, 0, 10}, AxesLabel -> {"t", "y[t]"}, PlotStyle->{Thick,Dashed}]

v[t_] = D[y[t], t]
Out[6]= 1/210 (14 Cos[5 t] Sin[3 t] + 50 Sin[5 t] - 14 Cos[3 t] Sin[5 t] + 6 Cos[7 t] Sin[5 t] - 6 Cos[5 t] Sin[7 t])
ParametricPlot[{y[t], v[t]}, {t, 0, 10}, AspectRatio -> 1, PlotStyle->{Thick,Brown}, AxesLabel -> {"y[t]", "v[t]"}, PlotLabel -> "v[t] vesus y[t]"]

 

 

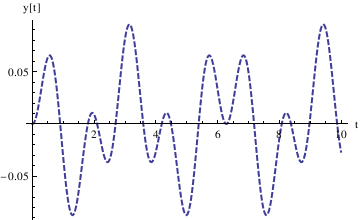
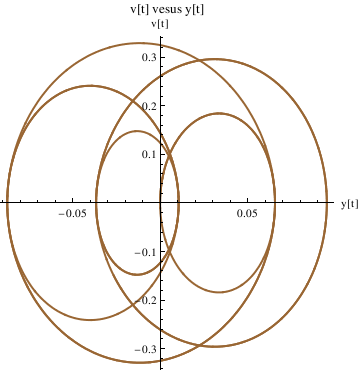
II. Aging Spring Equation

Consider the following spring equation with aging:

\[ \ddot{x} + 4\,e^{-t/4}\,x(t) =0 \qquad x(0) =1, \quad \dot{x} (0)=2 . \]

We solve it and plot in the following sequence of steps.

sol = DSolve[{x''[t] + 4*Exp[-t/4]*x[t] == 0, x[0] == 1, x'[0] == 2},
x, t] // InputForm
Out[1]=
{{x -> Function[{t}, (BesselJ[0, 16*Sqrt[E^(-t/4)]]*
BesselY[0, 16] - BesselJ[0, 16]*BesselY[0,
16*Sqrt[E^(-t/4)]] + BesselJ[1, 16]*
BesselY[0, 16*Sqrt[E^(-t/4)]] -
BesselJ[0, 16*Sqrt[E^(-t/4)]]*BesselY[1, 16])/
(BesselJ[1, 16]*BesselY[0, 16] - BesselJ[0, 16]*
BesselY[1, 16])]}}
Plot[x[t] /. sol[[1]], {t, 0, 30}]
Wrap sol =... in a bracket for clarity to obtain the same result:
(sol = DSolve[{x''[t] + 4*Exp[-t/4]*x[t] == 0, x[0] == 1, x'[0] == 2},
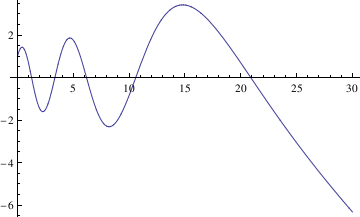
x, t]) // InputForm

f[t_] = x[t] /. sol[[1]]
f[0.5]

Out[5]= {1.40733}
f[0.5][[1]]
Out[6]= 1.40733
This gives 1.40733 without the curly brackets.

Another way to remove curly brackets:

f[t_] = x[t] /. sol[[1]][[1]]
Out[7]=
(BesselJ[0, 16 Sqrt[E^(-t/4)]] BesselY[0, 16] -
BesselJ[0, 16] BesselY[0, 16 Sqrt[E^(-t/4)]] +
BesselJ[1, 16] BesselY[0, 16 Sqrt[E^(-t/4)]] -
BesselJ[0, 16 Sqrt[E^(-t/4)]] BesselY[1, 16])/(BesselJ[1,
16] BesselY[0, 16] - BesselJ[0, 16] BesselY[1, 16])
f[0.5]
Out[8]= 1.40733

 

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value