Preface

This section discusses a pariticular example: rocking pendulum.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part IV of the course APMA0330

Glossary

Rocking Pendulum

plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{-2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{-0.85, 1.0}, {0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
makeArrowPlot[g_Graphics, ah_: 0.05, dx_: 1*^-6, dy_: 1*^-6] :=
Module[{pr = PlotRange /. Options[g, PlotRange], gg, lhs, rhs},
gg = g /. GraphicsComplex -> (Normal[GraphicsComplex[##]] &);
lhs := Or @@
Flatten[{Thread[Abs[#[[1, 1, 1]] - pr[[1]]] < dx], Thread[Abs[#[[1, 1, 2]] - pr[[2]]] < dy]}] &;
rhs := Or @@ Flatten[{Thread[Abs[#[[1, -1, 1]] - pr[[1]]] < dx], Thread[Abs[#[[1, -1, 2]] - pr[[2]]] < dy]}] &;
gg = gg /.
x_Line?(lhs[#] && rhs[#] &) :> {Arrowheads[{-ah, ah}], Arrow @@ x};
gg = gg /. x_Line?lhs :> {Arrowheads[{-ah, 0}], Arrow @@ x};
gg = gg /. x_Line?rhs :> {Arrowheads[{0, ah}], Arrow @@ x};
gg]
curve = Plot[{-Sqrt[9 - x^2]}, {x, -2.2, 2.2}, PlotStyle -> {Thick, Dashed}, Axes -> False] // makeArrowPlot
Show[a, line1, line2, curve]

Figure 1: Rocking rigid pendulum.

A rigid pendulum, such as a long rod, has a short cross-bar rigidly attached to it. As it oscillates in vertical plane, it is supported on ends of the cross-bar as they alternately contact a fixed horizontal surface:
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
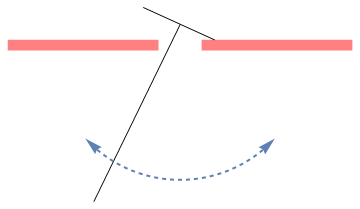
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{-2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{-0.85, 1.0}, {0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
p2 = Graphics[{Dashed, Arrow[{{-0.66, -0.8}, {-0.66, -3.8}}]}]
point = Graphics[{PointSize[Large], Green, Point[{-0.66, -0.8
t1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Red], {-1.0, -2.4}]]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {-1.0, -0.8}]]
a1 = Graphics[Text[Style["a", FontSize -> 14, Blue], {0.5, 0.7}]]
a2 = Graphics[Text[Style["a", FontSize -> 14, Blue], {-0.2, 1.0}]]
Q = Graphics[Text[Style["Q", FontSize -> 14, Blue], {1.0, 0.45}]]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {0.0, -0.2}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {-0.2, -3.6}]]
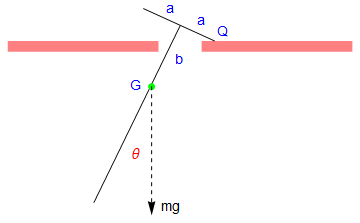
Show[a, line1, line2, point, p2, t1, t2, a1, a2, Q, b, mg]
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{0.85, 1.0}, {-0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
p2 = Graphics[{Dashed, Arrow[{{0.66, -0.8}, {0.66, -3.8}}]}]
point = Graphics[{PointSize[Large], Green, Point[{0.66, -0.8}]}]
t1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Red], {1.0, -2.4}]]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {0.3, -0.8}]]
P = Graphics[Text[Style["P", FontSize -> 14, Blue], {-0.9, 0.45}]]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {0.0, -0.2}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {0.22, -3.6}]]
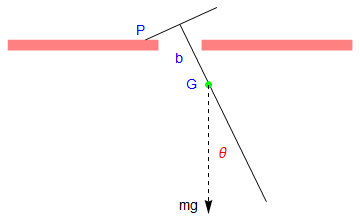
Show[a, line1, line2, point, p2, t1, t2, P, b, mg]
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{0, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{0.85, 0.27}, {-0.85, 0.27}}], PlotRange -> {{-2, 2}, {-4, 1}}]
P = Graphics[Text[Style["P", FontSize -> 14, Blue], {0.9, 0.45}]]
Q = Graphics[Text[Style["Q", FontSize -> 14, Blue], {-0.9, 0.45}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {0.4, -3.6}]]
point = Graphics[{PointSize[Large], Green, Point[{0, -0.8}]}]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {-0.3, -0.8}]]
p3 = Graphics[{Dashed, Line[{{0, -0.8}, {0.85, 0.27}}]}]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {-0.3, -0.2}]]
a1 = Graphics[Text[Style["a", FontSize -> 14, Blue], {0.3, 0.5}]]
a2 = Graphics[Text[Style["a", FontSize -> 14, Blue], {-0.3, 0.5}]]
ell = ToExpression["\ell", TeXForm]
t3 = Graphics[Text[Style[ell, FontSize -> 14, Black], {0.6, -0.4}]]
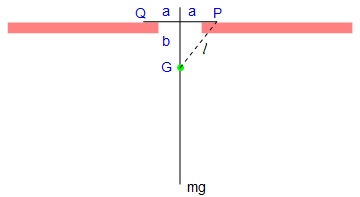
Show[a, line1, line2, point, p3, t2, a1, a2, P, Q, b, mg, t3]
     

Let the mass of the pendulum be m, and the length of the attached bar be 2 a. Since the construction of the rigid pendulum is symmetric, the center of gyration, which we denote by G, is along the main rod. Let k be the radius of gyration of the pendulum about G, so that the square of its radius of gyration about P and Q is \( k^2 + \ell^2 . \)

 

The first half-cycle of the motion

Suppose that the pendulum is set in motion from the central position with initial conditions

\[ \theta =0 \quad \mbox{and} \quad \dot{\theta} = \omega_1 \qquad\mbox{at} \quad t=0. \]
Since energy is assumed to be conservative, the total energy is a constant:
\[ \frac{1}{2}\, m \left( k^2 + \ell^2 \right) \dot{\theta}^2 + mg \left( a\,\sin \theta -b\,\cos \theta \right) = \mbox{constant} . \]
For small oscillations, powers of θ higher than the first may be neglected, yielding
\[ \left( k^2 + \ell^2 \right) \dot{\theta}^2 + 2ag \,\theta = \mbox{constant} \qquad\mbox{or} \qquad \dot{\theta}^2 + c^2 \theta = \mbox{constant} , \]
where \( c^2 = 2ga \left( k^2 + \ell^2 \right) . \) The initial conditions enable this to be written as
\[ \dot{\theta}^2 + c^2 \theta = \omega_1^2 , \]
When the pendulum first comes to rest, let
\[ t= \frac{1}{2}\,\tau_1 , \quad \theta = \theta_1 , \quad \dot{\theta} =0. \]
Then
\[ \dot{\theta}^2 + c^2 \theta = \omega_1^2 \qquad\Longrightarrow \qquad \theta_1 = \omega_1^2 / c^2 ., \]
Now
\begin{align*} \frac{1}{2}\,\tau_1 &= \int_0^{\theta_1} \, \frac{{\text d} \theta}{\dot{\theta}} = \int_0^{\theta_1} \, \frac{{\text d} \theta}{\sqrt{\omega_1^2 - c^2 \theta}} = \frac{2}{c^2} \left[ \sqrt{\omega_1^2 - c^2 \theta} \right]_{0}^{\theta_1} \\ &= \frac{2\omega_1}{c^2} = \frac{2\sqrt{\theta_1}}{c} . \end{align*}
Clearly, the time taken for θ to reach zero again will also be \( \frac{1}{2}\,\tau_1 , \) and the angular speed will then be ω1 again. Thus, the first "half period" of oscillation will be \( \tau_1 = 4 \sqrt{\theta_1} /c . \)

 

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)