This section paves the way towards developing efficient algorithms for solving systems of linear equations. In order to achieve this objective, we need three things. First, we need to determine what operations on linear systems do not change their solution sets. Second, we need to transfer the given system of linear equations into appropriate mathematical model that reflects the given system of equations along with its solution set. All information about a system of equations can be stored in a single matrix, known as the augmented matrix. Finally, we need to pass on safe operations on systems of equations into our mathematical model.

Recall that in this tutorial we employ the notation 𝔽 for one of the following fields: either ℚ for rational numbers, or ℝ for real numbers, or ℂ for complex numbers. However, most examples involve field ℤ of integer numbers for historical reasons and to simplify exposition.

This section is divided into a number of subsections, links to which are:

Duality in matrix/vector multiplication

Elementary reduction operations

Elementary row operations

Elementary column operations

 

Geometric Interpretation

Recall that a Cartesian product 𝔽n of n copies of field 𝔽 consists of all (ordered) n-tuples:
\[ \mathbb{F}^n= \mathbb{F} \times \mathbb{F} \times \cdots \times \mathbb{F} = \left\{ \left( x_1 , x_2 , \ldots , x_n \right) \ : \ x_1 , x_2 , \ldots , x_n \in \mathbb{F} \right\} . \]
A linear equation in the variables x₁, x₂, … , xn, where n is a positive integer, is an equation of the form \begin{equation} \label{EqRow.1} a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b , \end{equation} where 𝑎₁, 𝑎₂, … , 𝑎n are given scalars (real or complex numbers). These scalars are called the coefficients of Eq.\eqref{EqRow.1} and a given number b is known as the constant term of the equation.
The expression in left-hand side of Eq.(1) can be considered as either action of a linear functional on vector x or as a dot-roduct of two numerical vectors: a • x = 𝑎₁ · x₁ + 𝑎₂ · x₂ + ⋯ + 𝑎n · xn. Although linear functional or linear form is explained in detail later in Part 3, we just use this term to emphasize that the left-hand size of Eq.(1) is just a linear mapping 𝔽n ⇾ 𝔽 defined by the dot product: ϕ(x) = a • x (in applications, this function ϕ is usually denoted either by a✶ or as a bra-vector ⟨a∣). Then this equation can be written as
\[ {\bf a}^{\ast} ({\bf x}) = \langle {\bf a} \vert {\bf x} \rangle = b \qquad \mbox{or} \qquad {\bf a} \bullet {\bf x} = b . \]

Note that the dot-product defines metric or distance only when field 𝔽 is real, but in case of complex numbers, it is just a linear combination of the products of the vector's components. Equation (1) presents a linear equation in standard form where constant term b is separated by sign "=" from the linear combination of vectors a = (𝑎₁, 𝑎₂, … , 𝑎n) and x = (x₁, x₂, … , xn). The standard form requires that every independent variable appears in the equation only once. Since we are going to modify the linear equation (1), it is convenient to assume that the order in which summation is performed remains the same in further manipulations; so you can choose any order of summation, but you have to be consistent.

Any n-tuple of scalars (s₁, s₂, … , sn) that satisfy Eq.\eqref{EqRow.1} is called a solution of the linear equation. The set of all solutions (which is a flat affine subspace) of Eq.\eqref{EqRow.1} is called a hyperplane.

The word "affine" is Latin-French meaning "related to" or "having affinity with." Below we illustrate a 2-dimensional affine subspace contained within a 3D space. This could be any plane that (a) need not pass through the origin; and (b) that fits within the larger dimension.

Using ParametricPlot3D, we start with 50 points, p = p₀ + 𝑎*v₁ + b*v₂, where 𝑎 and b are, each, a set of 50 parameters taking (for convenience) any real value between -2 and 2. p₀, v₁ and v₂ are fixed vectors in ℝ³. The graphic this produces looks like a random cluster of points contained in a 3D box.

SeedRandom[38947];
p0 = {1, 2, 3};
v1 = {1, 0, 0};
v2 = {0, 1, 1};
pts = Graphics3D[{Red, PointSize -> Medium, Point[Transpose[(p0 + a*v1 + b*v2) /. {a -> RandomReal[{-2, 2}, 50], b -> RandomReal[{-2, 2}, 50]}]]}]
Figure 1: Cluster of points.

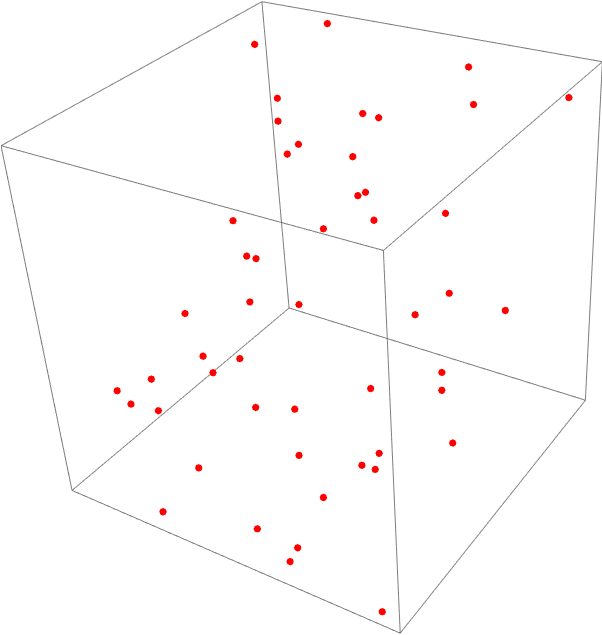
The notion of linearity imposes order on a system that otherwise appears random. Introducing a linear relationship between the fixed p₀, v₁ and v₂ vectors and the "random" 𝑎 and b through the parametric equation, results in points which fall on a common plane. Random is in quotes because the points are not completely random given that they are all forced onto a plane by the interaction with the vectors.

Below we rotate the graphic from above so that we see a "side view" of the cluster of points. It is clear that they are all on a single plane in the box which represents ℝ³ space.

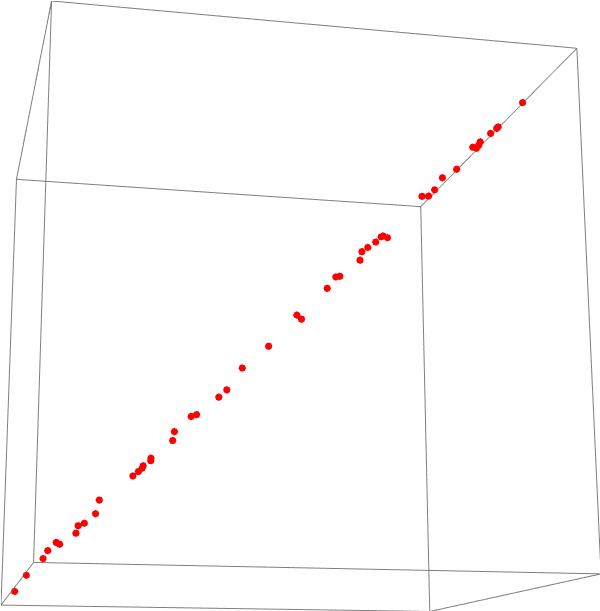
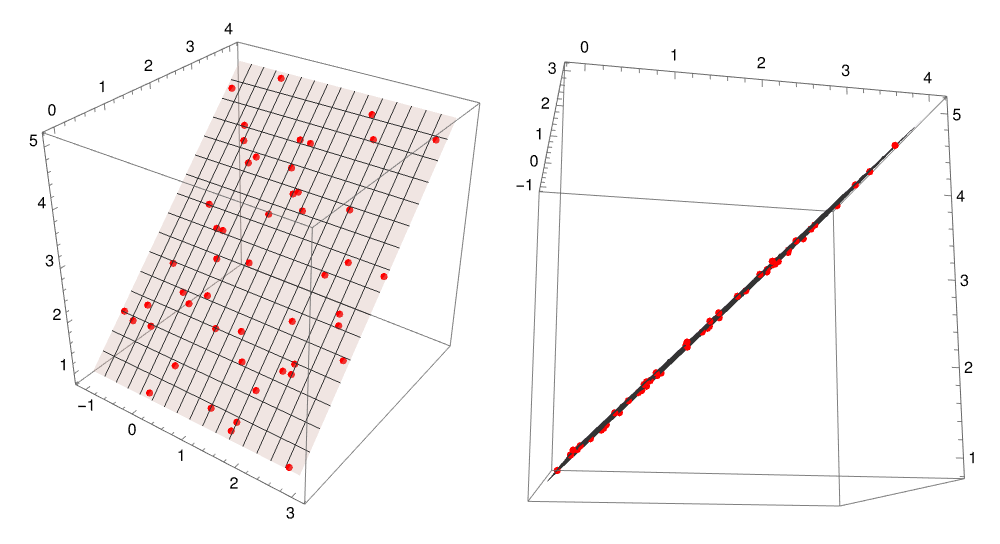
Graphics3D[{Red, PointSize -> Medium, Point[Transpose[(p0 + a*v1 + b*v2) /. {a -> RandomReal[{-2, 2}, 50], b -> RandomReal[{-2, 2}, 50]}]]}, ViewPoint -> {3.2240197785238074`, -0.6884799644316524, \ -0.762687227022640}]
Figure 2: Another view point on the cluster.

The illustrations above show only 50 points. Extending that to the plane described by the equation p = p₀ + 𝑎*v₁ + b*v₂ means choosing all possible points resulting from all possible values (between -2 and 2) that 𝑎 and b could take. Below on the left the same points in the graphic above are shown along with the parametric plot; on the right is the graphic on the left is again rotated to show the edge of the plane and the arrangement of all points on it.

pp3D = ParametricPlot3D[p0 + a*v1 + b*v2, {a, -2, 2}, {b, -2, 2}, Axes -> True, ViewPoint -> {1.6786479899281805`, -2.3402323843722823`, 1.7763595674990185`}, PlotStyle -> Directive[LightBlue, Opacity[0.3]]]; GraphicsRow[{Show[pp3D, pts], Show[pp3D, pts, ViewPoint -> {3.2240197785238074`, -0.6884799644316524, \ -0.762687227022640}]}]
Figure 3: Affine plane.

Unknown variables x₁, x₂, … , xn are also called the independent variables because they could be chosen arbitrary with only one condition that the expression in the left-hand side of Eq.\eqref{EqRow.1} is equal to the given constant term b. Any characters can be used for their notation, either indexed (what we prefer) or unlabeled. So Eq.\eqref{EqRow.1} can be written as

\[ a_1 田_1 + a_2 田_2 + \cdots + a_n 田_n = b \qquad\mbox{or} \qquad a_1 箱 + a_2 碗 + \cdots + a_n 杯 = b . \]
Since any software package uses only labeled arrays (known as lists), we prefer to use indexed variables. However, it is a customary to use notation x, y, and z for independent variables in three-dimensional space.

Since coefficients 𝑎₁, 𝑎₂, … , 𝑎n can be any scalars including zeroes, an expression of the form

\[ 0\cdot x_1 + 0\cdot x_2 + \cdots + 0 \cdot x_r + a_{r+1} x_{r+1} + \cdots + a_n x_n = b \]
is a legitimately formed linear equation. However, the first r variables do not effect the equation and can be chosen arbitrary. These r variables are called free variables. When r = n, Eq.\eqref{EqRow.1} is referred to as a degenerate linear equation. If b ≠ 0, the degenerate linear equation has no solution. If b = 0, the degenerate equation contains no information and can be dropped.

There are two particular cases that admit visualization of solutions to linear equation.

Example 1: Let us consider a linear equation with two unknowns \[ 2\,x + 3\, y = 4 . \] Mathematica can easily solve this equation
Solve[{2*x + 3*y == 4}, {x, y}]
{{y -> 4/3 - (2 x)/3}}
The command Flatten removes extra curly brackets in the output , but provides a warning message:
Flatten[Solve[{2*x + 3*y == 4}, {x, y}]]
Solve::svars: Equations may not give solutions for all "solve" variables.
{y -> 4/3 - (2 x)/3}
However, if you do not embrace the equation into cirly brackets, you get the same output:
Flatten[Solve[2*x + 3*y == 4, {x, y}]]
Solve::svars: Equations may not give solutions for all "solve" variables.
{y -> 4/3 - (2 x)/3}
In order to suppress warning message, you may want to combine Flatten[ ] with Quiet[]
Quiet[Solve[2*x + 3*y == 4, {x, y}]]
{{y -> 4/3 - (2 x)/3}}

Reduce is often better than Solve

Reduce[2*x + 3*y == 4, {x, y}]
y == 4/3 - (2 x)/3
So Mathematica defines x as a free/independent variable. When you read further you discover that the Gaussian elimination procedure refers to these independent variables as "free variables."
Figure 4: Solution of 2D equation.
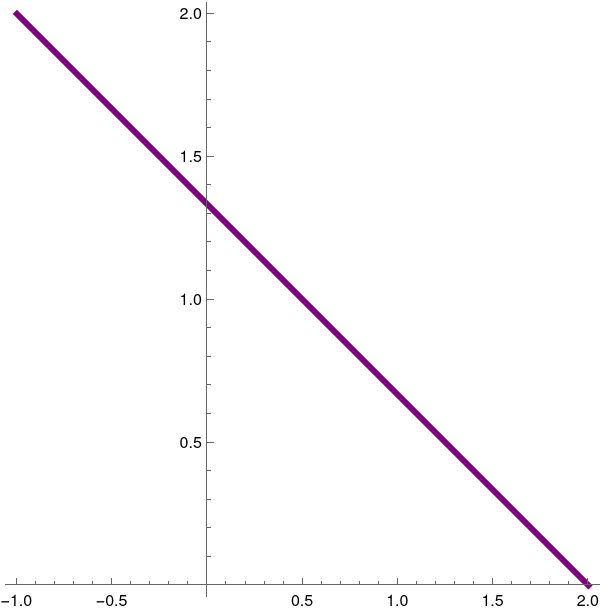
      We plot the hyperplane (which is a line) in ℝ² using the following Mathematica script.
Labeled[ContourPlot[{2*x + 3*y == 4}, {x, -2, 2}, {y, -2, 2}, ContourStyle -> {Purple, Thickness[0.01]}, PlotRange -> All, Axes -> True, Frame -> False], "Figure 4: Solution of 2D equation."]

In three-dimensional space, a linear equation \[ a\,x + b\, y + c\, z = d \] defines a hyperplane in ℝ³. For example, let us consider the equation \[ 2\, x - 3\, y + 4\, z = 5, \qquad x,y,z \in \mathbb{R} . \]

Figure 5: Solution of 3D equation.
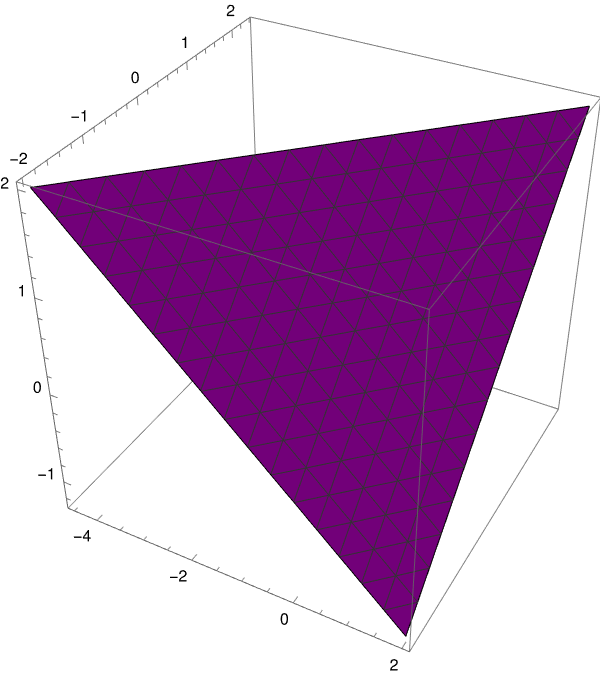
      We plot the hyperplane (which is a plane) in ℝ³ using the following Mathematica script.
Labeled[ContourPlot3D[ 2*x - 3*y + 4*z == 5, {x, -5, 2}, {y, -2, 2.5}, {z, -2, 2}, ContourStyle -> {Purple, Thickness[0.01]}, PlotRange -> All, Axes -> True], "Figure 5: Solution of 3D equation."]

End of Example 1

Now it is right time to discuss why solution set for 2D equation 𝑎 x + b y = c is a line (one-dimensional) while the plot of the linear equation 𝑎 x + b y + c z = d is a plane (two-dimensional). The reason lies in the fact that equation 𝑎 x + b y = c has one free variable and one dependent variable. The number of free variable of the linear equation in 3D is the number of degrees of freedom (which is the number of free variables (not containing pivots) in its row echelon form) in expressing the solution, so this number is two.

The dimension of a geometric object is the minimum number of degrees of freedom needed express the equation's solution points. Equivalently, the dimension of a geometric object is the minimum number of independent variables it takes to describe uniquely all of the points of the geometric object.

By independent variables we mean variables that do not depend on any constraint. By dependent variable, we mean variables that do depend on other variables or some constraints. If we see an expression such as z = f(x, y), then variable z is definitely a dependent variable because it depends on two other variables, x and y. Now it should be clear that a general linear equation

\[ a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b \]
has dimension n − 1 as a geometric object in n-dimensional space 𝔽n because there are n variables and only one constraint, the equation. For example, ℝ² is two-dimensional space and is often pictured as the xy-plane while ℝ³ is three-dimensional space and is pictured as the xyz-space.

If, for instance, 𝑎n ≠ 0, the points in ℝn of the form

\[ \left( x_1 , x_2 , \ldots , x_{n-1} , \ \frac{b}{a_n} - \frac{a_1}{a_n}\, x_1 - \frac{a_2}{a_n}\, x_2 - \cdots - \frac{a_{n-1}}{a_n}\, x_{n-1} \right) \]
satisfy the general linear equation \eqref{EqRow.1}. If 𝑎n = 0, then we can simply solve for another variable xk, where k ≠ n and 𝑎k ≠ 0. Otherwise, the equation is degenerate: 0 = b.

A system in standard form of m linear equations in n unknowns x₁, x₂, … , xn is a set of m equations of the form \begin{equation} \label{EqRow.2} \begin{split} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n &= b_1 , \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n &= b_2 , \\ \vdots & \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n &= b_m . \end{split} \end{equation} The numbers 𝑎i,j are known in advance and called coefficients of the system. The right-hand m-tuple (b₁, b₂, … , bm) is called the constant term and system (2) is referred to as an m × n system.
Sometimes a system of linear equations (2) is known as a set of simultaneous equations; such terminology emphases that a solution s = (s₁, s₂, … , sn) is an assignment of values to each of the n unknowns such that each and every equation holds with this assignment.

Each of m equations defines a hyperplane in n-dimensional space. Then the simultaneous solution or intersection set to a system of m linear equations is a geometric object of dimension at most n − m.

Since we discussed the two-dimensional case in the opening section, we just outline the main results. In xy-plane ℝ², a linear equation 𝑎 x + b y = c defines a straight line, which is a one-dimensional geometric object. The intersection set of two lines is usually a point---which is zero dimensional. If two lines are parallel and overlap, their intersection will be one-dimensional object---the line itself. However, if two lines are parallel, their intersection is empty (no dimension because cardinality of ∅ is zero).

Dimensions[\[EmptySet]]
{}
The intersection set of three random lines is usually empty.

A plane as a solution set of one linear equation 𝑎 x + b y + c z = d is two-dimensional. The intersection set of two planes is usually a one dimensional line unless they are parallel. Their intersection could be two-dimensional if two planes overlap or the empty set when they are parallel. The intersection set of three planes is usually a point that is zero dimensional. One can think of this situation as first intersecting two planes that results in a line and then intersecting the resulting line with the third plane, which is usually a point. The intersection set could also be the plane itself, which is two-dimensional, a line that is one-dimensional, or the empty set with no dimension. The intersection set of four planes is usually empty and has no dimension, although the intersection set could be of any dimension two or lower. Hopefully, you see a pattern developing in the following examples.

Example 2: We consider the following 2×3 system of linear equations \[ \begin{split} 3\,x - 2\,y + 5\,z &= 1, \\ 2\,x + 7\,y - 3\,z &= 2 . \end{split} \] Its solution set should be one-dimensional because planes 3 x − 2 y + 5 z = 1 and 2 x + 7 y − 3 z = 2 are linearly independent. The dimension of the solution set is the number of variables (which is 3) minus the number of equations in the system (which is 2), so 3 − 2 = 1.

The equation of this line of intersection can be found with the aid of Mathematica. Since there is only one free variable, it is up to you which one you choose. Let us start with z as an independent variable

Solve[{3*x - 2*y + 5*z == 1, 2*x + 7*y - 3*z == 2}, {x, y}]
{{x -> 1/25 (11 - 29 z), y -> 1/25 (4 + 19 z)}}
\[ x = \frac{1}{25} \left( 11 - 29\,z \right) , \qquad y = \frac{1}{25} \left( 4 + 19\,z \right) \] You can of course choose x as a free variable:
Solve[{3*x - 2*y + 5*z == 1, 2*x + 7*y - 3*z == 2}, {y, z}]
{{y -> 1/29 (13 - 19 x), z -> 1/29 (11 - 25 x)}}
\[ y = \frac{1}{29} \left( 13 - 19\,x \right) , \qquad z = \frac{1}{29} \left( 11 - 25\,x \right) \] When independent variable is y, we have
Solve[{3*x - 2*y + 5*z == 1, 2*x + 7*y - 3*z == 2}, {x, z}]
{{x -> 1/19 (13 - 29 y), z -> 1/19 (-4 + 25 y)}}
\[ x = \frac{1}{25} \left( 13 - 29\,y \right) , \qquad z = \frac{1}{25} \left( -4 + 25\,y \right) \]

Figure 6: Intersection of two hyperplanes.
      We plot the intersection of hyperplanes in ℝ³ using the following Mathematica script.
E1 = 3*x - 2*y + 5*z == 1;
E2 = 2*x + 7*y - 3*z == 2;
twoPlanes = ContourPlot3D[Evaluate[{E1, E2}], {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, ContourStyle -> {Yellow, Blue}, Mesh -> None, AspectRatio -> 1];
Labeled[%, "Figure 6: Intersection of two hyperplanes in Example 2."]

Figure 7: Solution set of Example 2.
     
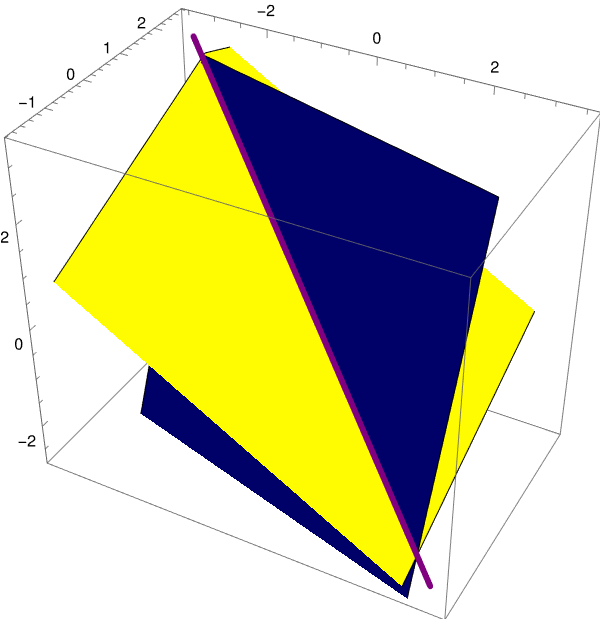
solnline = Solve[{E1, E2}, {x, y}][[1]]
{x -> 1/25 (11 - 29 z), y -> 1/25 (4 + 19 z)}
solplot = ParametricPlot3D[{x /. solnline[[1]], y /. solnline[[2]], z}, {z, -2.5, 3.2}, PlotStyle -> {{Purple, Thickness[0.01]}}];
Show[solplot, twoPlanes]

To solve the given system of linear equations by hand, we must first decide which variable we would like expressed in terms of the others. With our current system of two equations and three unknowns, we should be able to express two variables as a function of the third one in the final solution. We will choose to express the y and z variables in terms of x. A very simple way to do this is to move the x variable, along with its coefficient, to the right-hand side (RHS) of each equation. If we focus on the resulting left-hand side (LHS), then we obtain the problem with just two variables: \[ \begin{split} -2\,y + 5\,z &= 1 - 3\,x , \\ 7\,y - 3\, z &= 2- 2\,x . \end{split} \] To solve this system manually, we employ Chiò’s method; so we multiply the first equation by 7 and the second one by 2 and then add them. \[ \begin{split} 7 \left( -2\,y + 5\,z \right) &= 7 - 21\,x , \\ 2 \left( 7\,y - 3\, z \right) &= 4- 4\,x , \\ \hline 29\, z &= 11 - 25\, x . \end{split} \] Hence, from last equation, we obtain \[ z = \frac{1}{29} \left( 11 - 25\, x \right) . \] Substituting this expression into the first equation, we determine the value of another variable y.

End of Example 2
     
Example 3: Now let's add another plane and see whether we get a single point as solution We now attempt to solve and plot the linear system: \[ \begin{split} 3\,x - 2\,y + 5\,z &= 1, \\ 2\,x + 7\,y - 3\,z &= 2 , \\ 5\,x - 3\,y - 2\,z &= 4 . \end{split} \] We solve this system with Mathematica
Solve[{3*x - 2*y + 5*z == 1, 2*x + 7*y - 3*z == 2, 5*x - 3*y - 2*z == 4}, {x, y, z}]
{{x -> 59/84, y -> -(1/84), z -> -(19/84)}}
\[ x = \frac{59}{84}, \qquad y - \frac{1}{84}, \qquad z = -\frac{19}{84} . \]
E1 = 3*x - 2*y + 5*z == 1;
E2 = 2*x + 7*y - 3*z == 2;
E3 = 5*x - 3*y - 2*z == 4;
soln = Solve[{E1, E2, E3}, {x, y, z}][[1]]
{x -> 59/84, y -> -(1/84), z -> -(19/84)}
solpoint = {x /. soln[[1]], y /. soln[[2]], z /. soln[[3]]}
{59/84, -(1/84), -(19/84)}
thirdPlane = ContourPlot3D[Evaluate[E3], {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, ContourStyle -> {Red}, Mesh -> None];
solpointplot = Graphics3D[{White, Sphere[solpoint, 0.8]}];
Show[{twoPlanes, thirdPlane, solpointplot}, PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}, AspectRatio -> 1]
Figure 8: Solution set of Example 3.
End of Example 3
     
Example 4: Let us solve the 3 × 5 linear system given by \[ \begin{split} 3\,x - 2\,y + 5\,z - 4\,w + t &= 1, \\ 2\,x + 7\,y - 3\,z + 2\, w - 5\,t&= 2 , \\ 5\,x - 3\,y - 2\,z + w - 3\,t &= 4 . \end{split} \] Each of these linear equations represents a four-dimensional geometric object (a hyperplane in ℝ5). Since we have three linear equations, we expect the simultaneous solution to be a (5 − 3 = 2)-dimensional plane in ℝ5).
Solve[{3*x - 2*y + 5*z -4*w+t == 1, 2*x + 7*y - 3*z + 2*w- 5*t == 2, 5*x - 3*y - 2*z + w - 3*t == 4}, {x, y, z}]
{{x -> 1/252 (177 + 159 t + 25 w), y -> 1/252 (-3 + 87 t + w), z -> 1/252 (-57 - 111 t + 187 w)}}
This solution has three dependent variables x, y, and z, and two independent variables w and t. Hence, the dimension of the solution set is two.
End of Example 4
     

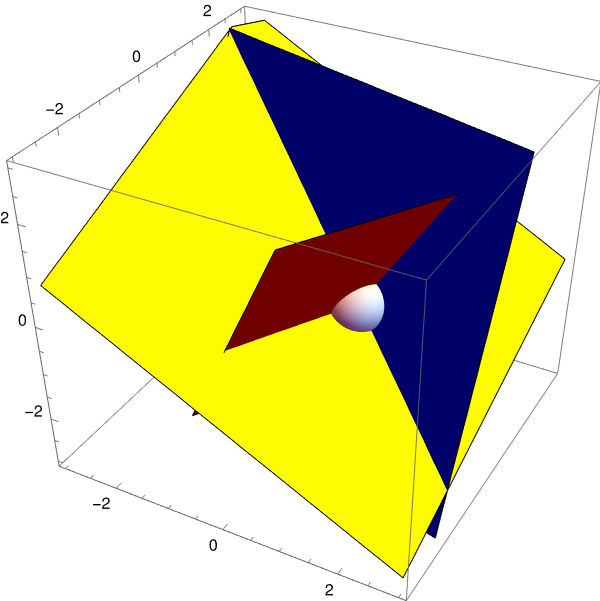
Duality in matrix/vector multiplication

  1. If A and b are the matrix and vector given by \[ {\bf A} = \begin{bmatrix} -1& -2& 3 & 1 \\ 7 & 5 & 6 & 1 \\ 9 & -2 & 3 & 4 \end{bmatrix} \quad \mbox{and} \quad {\bf b} = \begin{bmatrix} -1 \\ 2 \\ 8 \\ 5 \end{bmatrix}. \] What linear system (written out in full) corresponds to the vector equation A x = b ?
  2. If A and b are the matrix and vector given by \[ {\bf A} = \begin{bmatrix} 1&2&-3&7 \\ 9 &8&2&-3 \\ 2&5& -7 & 3 \end{bmatrix} \quad \mbox{and} \quad {\bf b} = \begin{bmatrix} 5 \\ 4 \\ 3 \\ 1 \end{bmatrix}. \] What linear system (written out in full) corresponds to the vector equation A x = b ?
  3. Find the coefficient matrix A, the variable vector x, and the right-hand side vector b for the following systems. \[ {\bf (a)\ \ \ } \begin{split} 3\,x_1 -2\,x_2 + 5\,x_4 &= 21, \\ 2\,x_2 - 4\,x_3 + x_5 &= -7 , \\ - x_1 + 3\,x_3 - 6\,x_4 &= 13; \end{split} \qquad {\bf (b)\ \ \ } \begin{split} x_1 - 3\,x_2 + 2\,x_3 - x_4 &= 22, \\ 3\,x_1 + x_2 - 2\, x_3 + 4\,x_4 &= -8, \\ -x_1 - 4\,x_2 + 3\,x_3 - 5\, x_4 &= 78. \end{split} \]
  4. Let x = (x, y, z) . Express the “row problem” \[ \begin{split} {\bf a}^{\ast}_1 ({\bf x}) &= -1 , \\ {\bf a}^{\ast}_2 ({\bf x}) &= 4 , \\ {\bf a}^{\ast}_3 ({\bf x}) &= 1 , \end{split} \] as a linear system, assuming that a₁ = (2, −4, 5), a₂ = (3, 1, −2), and a₃ = (−4, 5, 2).
  5. Let x = (x, y, z) . Express the “row problem” \[ \begin{split} {\bf a}^{\ast}_1 ({\bf x}) &= -7 , \\ {\bf a}^{\ast}_2 ({\bf x}) &= 14 , \\ {\bf a}^{\ast}_3 ({\bf x}) &= 31 , \end{split} \] as a linear system, assuming that a₁ = (2, −3, 2), a₂ = (3, 1, −9), and a₃ = (−1, 3, 6).
  6. Express the linear system below in “row” form \[ \begin{split} 2\,x - 3\,y + 5\,z &= 2, \\ 3\,x - 6\,y + 9\, z &= 8, \\ -x + 2\,y - 7\,z &= 3. \end{split} \]
  7. Express the linear system below in “column” form \[ \begin{split} -x + 9\,y + 2\, z &= 21 , \\ 2\,x - 8\,y + 3\,z &= 15, \\ 3\,x + 4\,y - 8\,z &= 27. \end{split} \]
  8. Express the “column problem” \[ {\bf a}_1 x_1 + {\bf a}_2 x_2 + {\bf a}_3 x_3 = {\bf b} \] as a linear system in the variables x₁, x₂, x₃, assuming a₁ = [6, −3, 5]T, a₂ = (7, 2, −3]T, and a₃ = [−2, 4, 3]T.
  9. Express the “column problem” \[ u\,{\bf a}_1 + v\,{\bf a}_2 + w\, {\bf a}_3 = {\bf b} \] as a row problem, where a₁ = [3, −1, 4]T, a₂ = (3, 8, −9]T, a₃ = [−4, 5, 6]T, and b [3, 2, 5]T.
  10. What linear combinations (if any) of the vectors (3, 1, 2, 4), (1, 6, 5, 3), and (4, 3, 1, 6) add up to (7, −2, 5, 3)?
  11. Find the matrix that results from performing the indicated elementary row operation.
    1. \( \displaystyle \begin{bmatrix} 2&7&4 \\ 0&3&1 \\ 3&2&3 \end{bmatrix} \qquad \) R3 ← R3 + (−3/2)·R1;
    2. \( \displaystyle \begin{bmatrix} 1&7&3 \\ 2&3&-1 \\ 0&4&6 \end{bmatrix} \qquad \) R2 ← R2 −2·R1;
    3. \( \displaystyle \begin{bmatrix} 3&4&2 \\ 0&1&7 \\ 1&3&8 \end{bmatrix} \qquad \) R3 ← R3 + (−1/3)·R1;
    4. \( \displaystyle \begin{bmatrix} 1&2&6 \\ 0&1&5 \\ 0&4&3 \end{bmatrix} \qquad \) R3 ← R3 −4·R2;
    5. \( \displaystyle \begin{bmatrix} 7&6&5 \\ 0&4&3 \\ 0&2&7 \end{bmatrix} \qquad \) R3 ← R3 −2·R2;
    6. \( \displaystyle \begin{bmatrix} 1&5&2 \\ 0&1&1 \\ 0&7&4 \end{bmatrix} \qquad \) R3 ← R3 −7·R2.
  12. Find the matrix that results from performing the indicated elementary row operation.
    1. \( \displaystyle \begin{bmatrix} 3&0&8 \\ 2&-4&2 \end{bmatrix} \qquad \) R1 ↑ R2;
    2. \( \displaystyle \begin{bmatrix} 1&2&3&4 \\ 0&3&5&2 \\ 3&7&0&4 \end{bmatrix} \qquad \) R3 ← R3 − 3·R1;
    3. \( \displaystyle \begin{bmatrix} 1&3&4&2&1 \\ 0&1&5&2&3 \\ 0&-1&4&2&-1 \end{bmatrix} \qquad \) R3 ← R3 − ;R1;
    4. \( \displaystyle \begin{bmatrix} 1&2&-4&5 \\ 0&3&8&10 \end{bmatrix} \qquad \) R2 ← R2 + 2·R1;
    5. \( \displaystyle \begin{bmatrix} 1&1&3 \\ 5&5&21 \end{bmatrix} \qquad \) R2 ← R2 − 5·R1;
    6. \( \displaystyle \begin{bmatrix} 1&-2&5&7 \\ 0&1&3&5 \\ 0&0&1&3 \end{bmatrix} \qquad \) R3 ← R3 + (−1/2)·R2.
  13. identify the elementary row operation (by Type and by action) that transforms the matrix on the left into the matrix on the right.
    1. \( \displaystyle \begin{bmatrix} 3&1&2&3 \\ 1&2&1&5 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 3&1&2&3 \\ 1&2&1&5 \end{bmatrix} \qquad \)
    2. \( \displaystyle \begin{bmatrix} 1&2&3&1 \\ 0&2&1&2 \\ 0&6&3&7 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 1&2&3&1 \\ 0&2&1&2 \\ 0&0&0&1 \end{bmatrix} \qquad \)
    3. \( \displaystyle \begin{bmatrix} 1&2&2&2&4 \\ 3&2&1&3&3 \\ 0&1&1&2&2 \\ 0&4&2&2&1 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 1&2&2&2&4 \\ 3&2&1&3&3 \\ 3&0&-1&-1&-1 \\ 0&1&1&2&2 \\ 0&4&2&2&1 \end{bmatrix} \qquad \)
    4. \( \displaystyle \begin{bmatrix} 1&2&1&5 \\ 0&-5&-1&-12 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 1&2&1&5 \\ 0&1&0.2&2.4 \end{bmatrix} \qquad \)
    5. \( \displaystyle \begin{bmatrix} 1&2&1&5 \\ 3&1&2&3 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 1&2&1&5 \\ 0&-5&-1&-12 \end{bmatrix} \qquad \)
    6. \( \displaystyle \begin{bmatrix} 1&2&1&5 \\ 0&1&0.2&2.4 \end{bmatrix} \qquad \) and \( \displaystyle \quad \begin{bmatrix} 1&0&0.6&0.2 \\ 0&1&0.2&2.4 \end{bmatrix} \qquad \)
  14. Determine whether or not the given vector is a solution to the system: \[ \begin{split} x+ 2\,y - 3\, z &= 0 , \\ 2\,x - 3\,y + z &= 0 . \end{split} \] \[ {\bf (a)\ \ } \left( 3, 3, 3 \right) , \qquad {\bf (b)\ \ } \left( 1, 2, 3 \right) . \]
  15. Determine whether or not the given vector is a solution to the system: \[ \begin{split} x + 2\, y - 4\,z &= 0, \\ 3\,x = 5\,y + 2\, z &= 0 . \end{split} \] \[ ({\bf a}) \quad \begin{bmatrix} 11 \\ 16 \\ 14 \end{bmatrix} , \qquad ({\bf b}) \quad \begin{bmatrix} 16 \\ 14 \\ 11 \end{bmatrix} , \qquad ({\bf c}) \quad \begin{bmatrix} 14 \\ 16 \\ 11 \end{bmatrix} . \]
  16. Determine whether or not the given vector is a solution to the system: \[ \begin{split} x + 2\, y - 4\,z &= 3, \\ 3\,x = 5\,y + 2\, z &= 2 . \end{split} \] \[ ({\bf a}) \quad \begin{bmatrix} 9 \\ 7 \\ 5 \end{bmatrix} , \qquad ({\bf b}) \quad \begin{bmatrix} 16 \\ 14 \\ 11 \end{bmatrix} , \qquad ({\bf c}) \quad \begin{bmatrix} 4 \\ 6 \\ 11 \end{bmatrix} . \]
  17. Show that the following pairs of matrices are row equivalent by finding a sequence of one or more elementary row operations that transforms the first matrix into the second matrix. \[ ({\bf a})\quad \begin{bmatrix} 1&3&2 \\ 0&1&1 \end{bmatrix} , \quad \begin{bmatrix} 1&0&-1 \\ 0&1&1 \end{bmatrix} ; \qquad ({\bf b})\quad \begin{bmatrix} 2&7&1 \\ 1&5&4 \end{bmatrix} , \quad \begin{bmatrix} 1&5&4 \\ 2&7&1 \end{bmatrix} ; \] \[ ({\bf c})\quad \begin{bmatrix} 1&1&3 \\ 0&1&1 \\ 0&0&1 \end{bmatrix} , \quad \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} ; \qquad ({\bf d})\quad \begin{bmatrix} 1&2&1 \\ 2&0&3 \\ 3&7&4 \end{bmatrix} , \quad \begin{bmatrix} 1&2&1 \\ 0&-4&1 \\ 0&1&1 \end{bmatrix} ; \] \[ ({\bf e})\quad \begin{bmatrix} 1&3&1&5 \\ 1&0&-11&-1 \\ 0&4&2&1 \\ 0&0&1&2 \end{bmatrix} , \quad \begin{bmatrix} \end{bmatrix} ; \qquad ({\bf f})\quad \begin{bmatrix} \end{bmatrix} 1&0&1 \\ 0&1&2, \quad \begin{bmatrix} 1&2&5 \\ 2&5&12 \end{bmatrix} . \]

 

  1. Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
  2. Beezer, R., A First Course in Linear Algebra, 2015.
  3. Beezer, R., A Second Course in Linear Algebra, 2013.
  4. Boelkins, M.R., Goldberg, J.I., Potter, M.C., Differential Equations with Linear Algebra, Mathematica Help, 2009.
  5. Osgood, William F. (1919). "The life and services of Maxime Bôcher". Bull. Amer. Math. Soc. 25 (8): 337–350. doi:10.1090/s0002-9904-1919-03198-x.