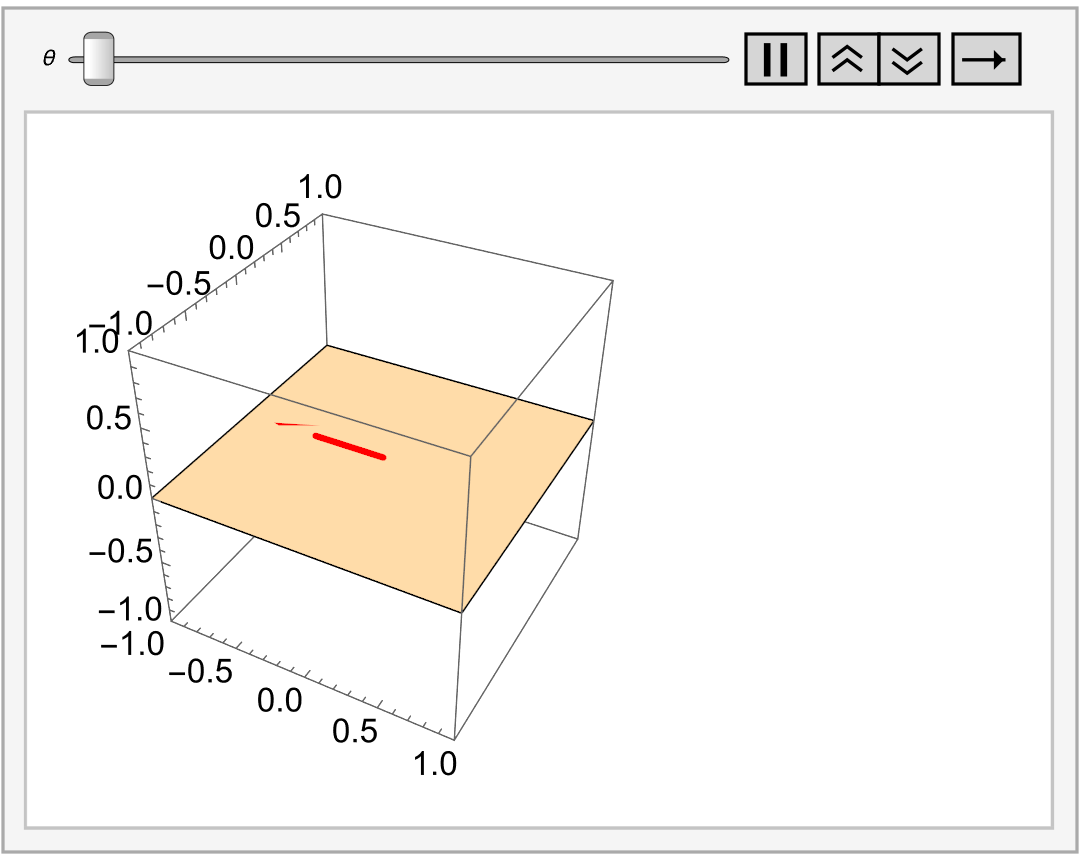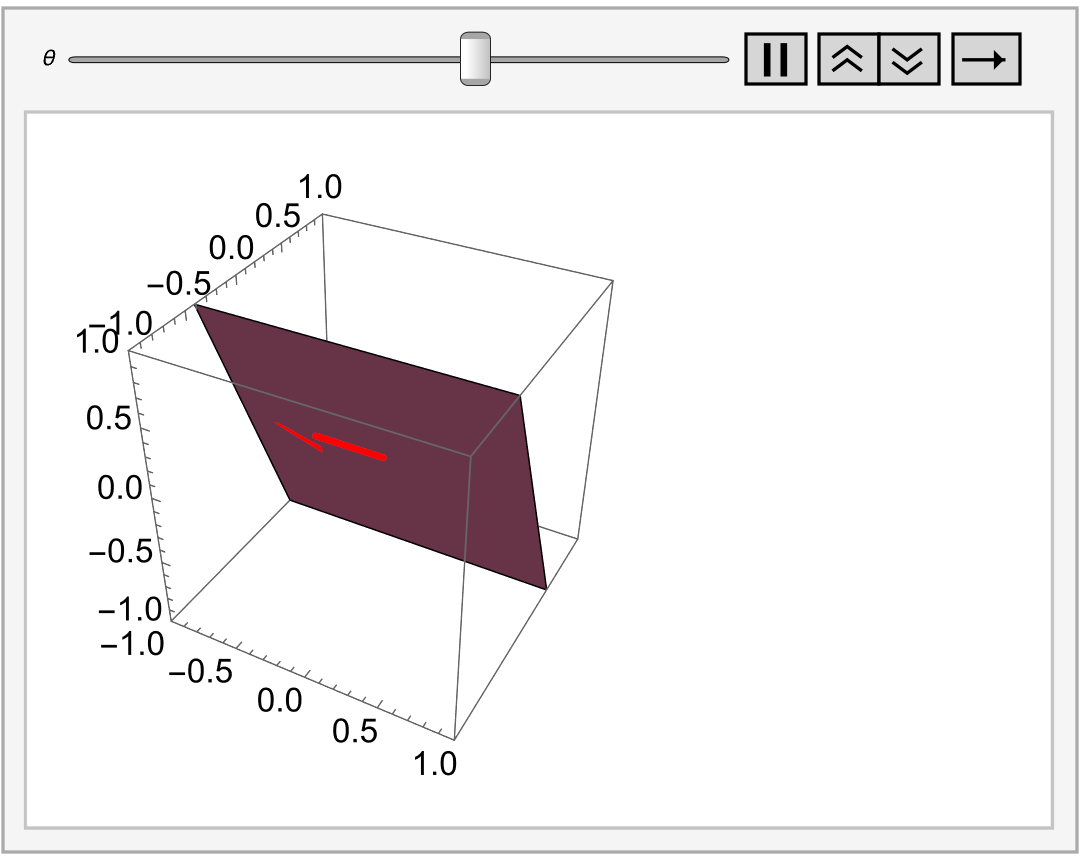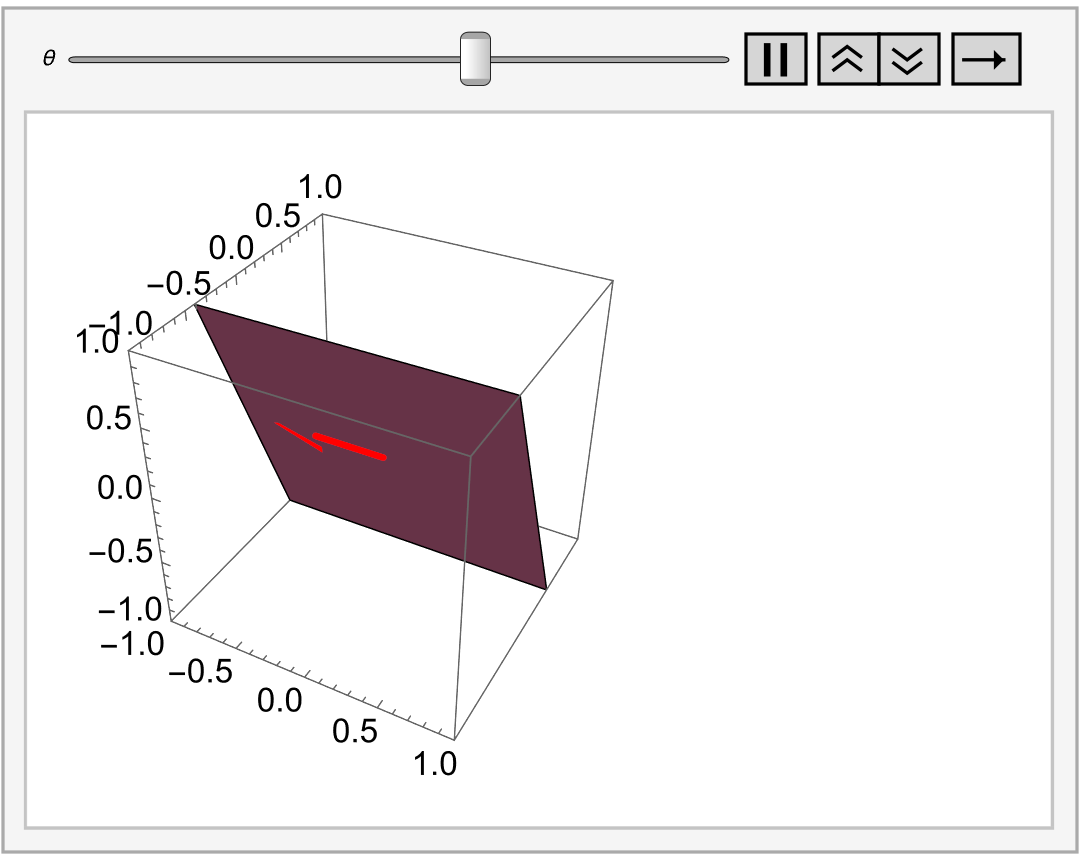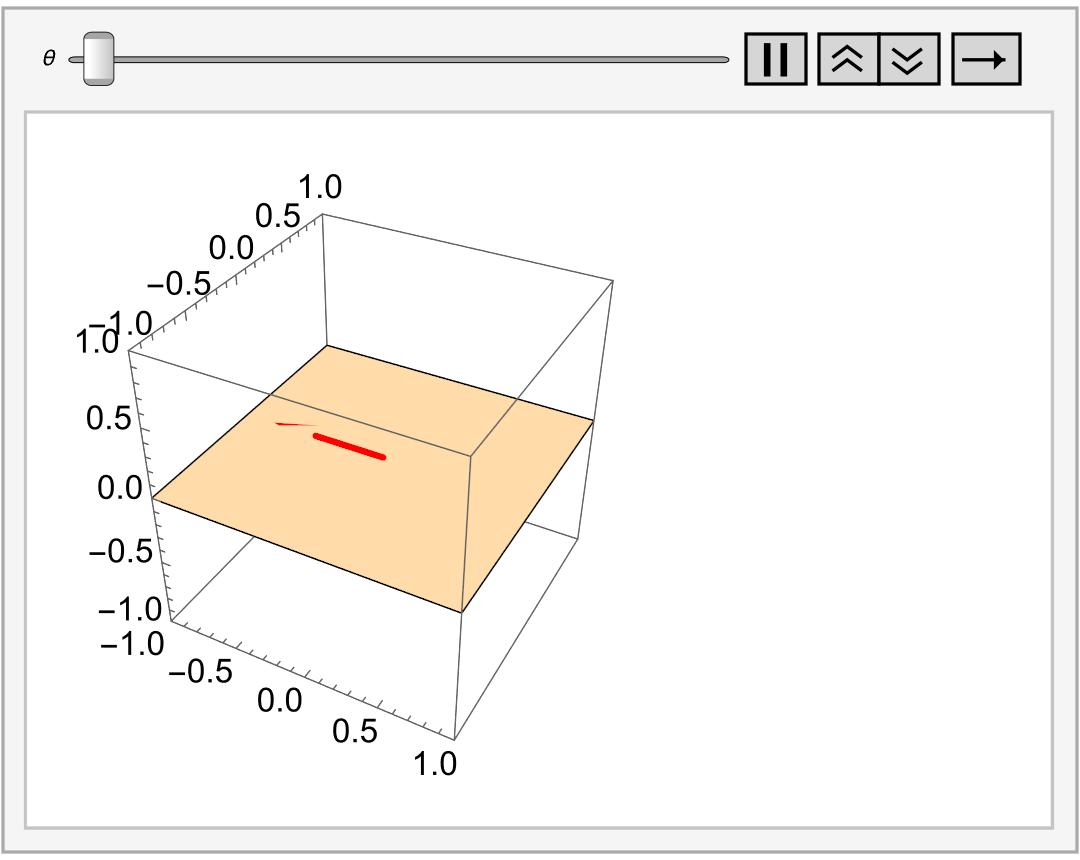
A vector subspace W ⊂ V can be used to define an equivalence relation on V. The associated equivalence classes are called cosets or affine k-planes.
The quotient V/W forms a vector space with dimension dim(V) − dim(W). The elements of the quotient vector spaceV/W are equivalence classes of vectors under an equivalence relation which declares two vectors
as related if their difference is contained in the vector subspace W. The construction
leads to an elegant proof of the isomorphism and rank theorems.
Quotient Spaces
Consider a vector space V and a vector subspace W ⊂ V with dimension k = dim(W). We say that two vectors in V are related if their difference is a vector in W, so
\[
{\bf v} \,\sim \,{\bf u} \qquad \iff \qquad {\bf v} - {\bf u} \in W.
\]
- Lukas, A., The Oxford Linear Algebra for Scientists, Oxford University Press, Oxford.2022.