Preface

This tutorial was made solely for the purpose of education and it was designed for students taking Applied Math 0330. It is primarily for students who have very little experience or have never used Mathematica before and would like to learn more of the basics for this computer algebra system. As a friendly reminder, don't forget to clear variables in use and/or the kernel.

Finally, the commands in this tutorial are all written in bold black font, while Mathematica output is in normal font. This means that you can copy and paste all commands into Mathematica, change the parameters and run them. You, as the user, are free to use the scripts for your needs to learn the Mathematica program, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0330
Return to Part IV of the course APMA0330

Pendulum

 

I. Pendulum Equation

The simple pendulum is of historic and basic importance. Its approximate isochronism, was first discovered by Galileo, who is said to check the constancy of the period of the small oscillations of a pendulum by comparing them with his heartbeat. In hands of Newton, pendulum provided the first evidence that inertial and gravitational masses are proportional. Until relatively recently, the plane pendulum yielded the most accurate and convenient method for measuring the local gravitational acceleration.
Christiaan Huygens.

There is no doubt that the first person who investigated and established the mathematical theory and properties of the pendulum was a prominent Dutch mathematician and scientistt named Christiaan Huygens (this spelling of his name is taken from the title of his 1658 book Horologium Oscillatorium). The main point of Huygens' (1629--1695) discovery was that the curve in which a pendulum particle (or bob) hangs by a string of insensible weight must move in order to be isochronous in its vibrations, and is not a circle, but a cycloid.

The pendulum consists of a bob of mass m attached to the end of a light inextensible rod of length \( \ell \) with the motion taking place in a vertical plane. Such pendulum is usually referred to as a simple pendulum. Let θ be the angular coordinate of m measured counterclockwise from the down position. The kinetic and potential energies are

\[ \mbox{K} = \frac{1}{2}\, I_0 \dot{\theta}^2 , \qquad\mbox{and} \qquad \Pi = mgy = mg\ell \left( 1- \cos \theta \right) , \]
where \( I_0 = m\ell^2 \) is the moment of inertia of the pendulum. Calculating partial derivatives, we get
\[ \frac{\partial \mbox{K}}{\partial \dot{\theta}} = I_0 \dot{\theta} = m\ell^2 \dot{\theta} , \qquad \frac{\partial \Pi}{\partial \theta} = mgy = mg\ell \, \sin \theta . \]
Using these expressions, we obtain from the Euler--Lagrange equation \( \displaystyle \frac{\text d}{{\text d} t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}} \right) = \frac{\partial {\cal L}}{\partial \theta} , \) for the Lagrangian \( {\cal L} = \mbox{K} - \Pi , \) the pendulum equation in a vacuum:
\[ \ddot{\theta} + \left( g/\ell \right) \sin \theta =0 \qquad \mbox{or} \qquad \ddot{\theta} + \omega_0^2 \sin \theta =0 , \]
where \( \ddot{\theta} = {\text d}^2 \theta / {\text d}t^2 \) , \( \omega_0 = \sqrt{g/\ell} >0 ,\) and g is gravitational acceleration. For small oscilaltions, we can replace sine function by its linear approximation, which leads to a linear differential equation
\[ \ddot{\theta} + \left( g/\ell \right) \theta =0 \qquad \Longleftrightarrow \qquad \ddot{\theta} + \omega_0^2 \theta =0. \]
We assume that the oscillations of the pendulum are subjected to the initial conditions \( \theta(0) = \theta_0 , \qquad \dot{\theta}(0) =0, \) where θ0 is the initial amplitude of the oscillation. The system oscillates between symmetric limits \( [- \theta_0 , \theta_0 ] . \) The periodic motion exhibited by a simple pendulum is harmonic only for small angle oscillations. Beyond this limit, the equation of motion is nonlinear: the simple harmonic motion is unsatisfactory to model the pendulum motion for large amplitudes and in such cases the period depends on amplitude. The periodic solution \( \theta (t) \) and the angular frequency ω (also with the period \( T = 2\pi /\omega \) ) depends on the initial amplitude \( \theta_0 . \)

Simple pendulum equation \( \ddot{\theta} + \omega_0^2 \sin \theta =0 , \) although straightforward in appearance, is in fact rather difficult to solve because of the non-linearity of the term \( \sin \theta . \) In order to obtain the exact solution, this equation is multiplied by the integrating factor \( \dot{\theta} = {\text d}\theta / {\text d} t, \) so that it becomes

\[ \dot{\theta} \,\ddot{\theta} + \dot{\theta}\, \sin\theta =0 , \]
which can be rewritten as
\[ \frac{{\text d}}{{\text d}t} \left[ \frac{1}{2} \left( \frac{{\text d} \theta}{{\text d}t} \right)^2 - \omega_0^2\, \cos\theta \right] =0 . \]
This equation, which corresponds to the conservation of the mechanical energy, is immediately integrable, taking into account the initial conditions:
\[ \left( \frac{{\text d} \theta}{{\text d}t} \right)^2 = 2\,\omega_0^2\left( \cos\theta - \cos \theta_0 \right) , \]
which can be written as follows:
\[ \left( \frac{{\text d} \theta}{{\text d}t} \right)^2 = 4\,\omega_0^2\left( \sin^2 \left( \frac{\theta_0}{2} \right) - \sin^2 \left( \frac{\theta}{2} \right) \right] , \]
where we used the trigonometric identity \( \cos \theta = 1 - 2\,\sin^2 \frac{\theta}{2} . \) Now let
\[ y = \sin \left( \frac{\theta}{2} \right) \qquad\mbox{and} \qquad k= \sin \left( \frac{\theta_0}{2} \right) . \]
Then \( y(0) = \sqrt{k} . \) It is easy to obtain \( {\text d}\theta / {\text d}t \) as a function of \( {\text d}y / {\text d}t \) as follows:
\[ \frac{{\text d}y}{{\text d}t} = \frac{{\text d}y}{{\text d}\theta} \, \frac{{\text d}\theta}{{\text d}t} = \frac{1}{2}\, \frac{{\text d}\theta}{{\text d}t} \,\cos \left( \frac{\theta}{2} \right) . \]
Then square it, we have
\[ \left( \frac{{\text d}y}{{\text d}t} \right)^2 = \frac{1}{4} \, \cos^2 \left( \frac{\theta}{2} \right) \left( \frac{{\text d}\theta}{{\text d}t} \right)^2 = \frac{1}{4} \left[ 1 - \sin^2 \left( \frac{\theta}{2} \right) \right] \left( \frac{{\text d}\theta}{{\text d}t} \right)^2 = \frac{1}{4} \left( 1 - y^2 \right) \left( \frac{{\text d}\theta}{{\text d}t} \right)^2 . \]
Its square derivative will be
\[ \left( \frac{{\text d}\theta}{{\text d}t} \right)^2 = \frac{4}{1-y^2} \left( \frac{{\text d}y}{{\text d}t} \right)^2 . \]
Substituting this relation into the integrated pendulum equation, we obtain
\[ \frac{4}{1-y^2} \left( \frac{{\text d}y}{{\text d}t} \right)^2 = 4\,\omega_0^2 \left( k - y^2 \right) , \]
which can be rewritten as
\[ \left( \frac{{\text d}y}{{\text d}t} \right)^2 = \omega_0^2 k \left( 1 - y^2 \right) \left( 1 - \frac{y^2}{k} \right) . \]
To simplify the above expression, we define new variables
\[ \tau = \omega_0 t \qquad\mbox{and}\qquad z = \frac{y}{\sqrt{k}} . \]
This leads to
\[ \left( \frac{{\text d}z}{{\text d}\tau} \right)^2 = \left( 1 - z^2 \right) \left( 1 - k\,z^2 \right) , \qquad z(0) = 1, \quad \left. \frac{{\text d}z}{{\text d}\tau} \right\vert_{\tau =0} =0. \]
Separation of variables yields
\[ {\text d}\tau = \pm \frac{{\text d}z}{\sqrt{\left( 1 - z^2 \right) \left( 1 - k\,z^2 \right)}} . \]
The time τ to go from point (1,0) to point \( \left( z, {\text d}z / {\text d} \tau \right) \) in the lower half-plane of the graph of \( {\text d}z / {\text d} \tau \) as a function of z is
\[ \tau = -\int_1^z \frac{{\text d}\zeta}{\sqrt{\left( 1 - \zeta^2 \right) \left( 1 - k\,\zeta^2 \right)}} . \]
We rewrite the integral in the right hand side as
\[ \tau = \int_0^1 \frac{{\text d}\zeta}{\sqrt{\left( 1 - \zeta^2 \right) \left( 1 - k\,\zeta^2 \right)}} - \int_0^z \frac{{\text d}\zeta}{\sqrt{\left( 1 - \zeta^2 \right) \left( 1 - k\,\zeta^2 \right)}} , \]
which allows us to obtain τ as a function of z and k as
\[ \tau (z) = K(k) - F(\arcsin z, k ) , \]
where K(m) and F(φ , m) are the complete and the incomplete elliptic integral of the first kind defined as follows
\begin{eqnarray*} K(m) &=& \int_0^1 \frac{{\text d}\zeta}{\sqrt{\left( 1 - \zeta^2 \right) \left( 1 - m\,\zeta^2 \right)}} \\ F(\phi , m) &=& \int_0^{\phi} \frac{{\text d}\zeta}{\sqrt{\left( 1 - \zeta^2 \right) \left( 1 - m\,\zeta^2 \right)}} , \qquad z= \sin \phi . \end{eqnarray*}
The period of oscillation T is four times the time taken by the pendulum to swing from \( \theta =0 \ (z=0) \) to \( \theta = \theta_0 \ (z=1) . \) Therefore,
\[ T = 4\,t(0) = \frac{4\,\tau (0)}{\omega_0} = \frac{4}{\omega_0} \,K(k) = \frac{2}{\pi}\, T_0 \,K(k) = \sqrt{\frac{\ell}{g}} \,\int_0^{\pi /2} \frac{{\text d} \beta}{\sqrt{1- k^2 \sin^2 \beta}} , \]
where
\[ T_0 = \frac{2\pi}{\omega_0} = 2\pi \,\sqrt{\frac{\ell}{g}} \]
is the period of the pendulum for small oscillations. The solution formula can be rewritten as
\[ F \left( \arcsin z , k \right) = K(k) - \tau , \]
which can be written in terms of the Jacobi elliptic function sn(u;m):
\[ z = \mbox{sn} \left( K(k) - \tau ; k \right) , \]
where Mathematica has special commands for their evaluations: EllipticK[m] for complete elliptic integral of the first kind, and EllipticF[φ,m] for incomplete elliptic integral of the first kind. Mathematica also uses a special command JacobiSN[u,m] for the Jacobi elliptic function sn(u;m). These functions are discussed in the second part of the course.

Now we return to the original variables
\[ \sin \left( \frac{\theta}{2} \right) = \sin \frac{\theta_0}{2} \, \mbox{sn} \left[ K\left( \sin^2 \frac{\theta_0}{2} \right) - \omega_0 t ; \sin^2 \frac{\theta_0}{2} \right] , \]
which allows us to express θ as a function of t:
\[ \theta (t) = 2\,\arcsin \left\{ \sin\frac{\theta_0}{2} \, \mbox{sn} \left[ K\left( \sin^2 \frac{\theta_0}{2} \right) - \omega_0 t ; \sin^2 \frac{\theta_0}{2} \right] \right\} . \]
Using the relations \( \dot{\bf e}_{r} = \dot{\theta} {\bf e}_{\theta} \) and \( \dot{\bf e}_{\theta} = -\dot{\theta} {\bf e}_{r} , \) we obtain the velocity, acceleration, and jerk:
\begin{eqnarray*} {\bf v} (t) &=& \ell \dot{\theta} {\bf e}_{\theta} = \sqrt{2\ell g} \left( \cos \theta - \cos \theta_0 \right)^{1/2} {\bf e}_{\theta} , \\ {\bf a} (t) &=& \dot{\bf v} (t) = -\ell \dot{\theta}^2 {\bf e}_{r} + \ell \ddot{\theta} {\bf e}_{\theta} = - 2g \left( \cos \theta - \cos \theta_0 \right) {\bf e}_{r} - g \,\sin \theta \, {\bf e}_{\theta} , \\ {\bf j} (t) &=& \dot{\bf a} (t) = 3g\,\sin\theta \, \dot{\theta} \, {\bf e}_r - \dot{\theta} \left[ 2\ell \dot{\theta}^2 + g\,\sin \theta \right] {\bf e}_{\theta} . \end{eqnarray*}
Manipulate[
Module[{run, sol, z, app, a},
If[run == 10, run = 0];
sol = DSolve[{y''[x] + (9.8/l)*y[x] == 0, y[0] == int, y'[0] == 0}, y, x];
z[x_] := y[x] /. sol;
app = NDSolve[{\[Theta]1''[t] + (9.8/l)*Sin[\[Theta]1[t]] == 0, \[Theta]1[0] == int, \[Theta]1'[0] == 0}, \[Theta]1, {t, 0, 10}];
a[t_] := \[Theta]1[t] /. First[app];
Grid[{{
Graphics[{
{Thick, Line[{{0, 0}, {l*Sin[a[r]], -l*Cos[a[r]]}}]}, {Darker[Green], Disk[{0, 0}, .03]}, {Purple,
Disk[{l*Sin[a[r]], -l*Cos[a[r]]}, 0.1 Power[(30 m)/(4 \[Pi]), (3)^-1]]}},
PlotRange -> {{-3.4, 3.4}, {.5, -3.4}},
ImageSize -> {250, 250}],
Plot[{a[t], z[t]}, {t, 0, 10},
PlotRange -> {{0, 10}, {-1.6, 1.6}},
PlotStyle -> {{Thick, Blue}, {Red}}, ImageSize -> {250, 250},
AspectRatio -> 1.2, Frame -> True,
PlotLegends`PlotLegend -> {"numerical", "sin(\[Theta]) = \[Theta]"},
FrameLabel -> {"time", "displacement"},
Epilog -> {Blue, PointSize[.06], Point[{r, a[r]}]}]}}]],
{{int, \[Pi]/3., "initial angle \[Theta](0)"}, \[Pi]/16., \[Pi]/2., Appearance -> "Labeled"},
Delimiter,
{{m, 4, "mass m"}, 1, 10, .01, Appearance -> "Labeled"},
{{l, 2.25, "length L"}, 1, 3, .01,
Appearance -> "Labeled"}, {{r, 0, "release system"}, 0, 10, .01,
ControlType -> Trigger, AnimationRate -> .5},
TrackedSymbols :> {int, m, l, r},
Initialization :> Get["PlotLegends`"]]

 

II. Pendulum Equation with Resistance

The resistance of the air acts on both the pendulum ball and the pendulum wire. It causes the amplitude to decrease with time and increases the period of oscillation slightly. The drag force is proportional to the velocity for values of the Reynolds number of the order 1 or less. For values of the Reynolds number of order \( 10^3 \) to \( 10^5 , \) the force is proportional to the square of the velocity. The maximum Reynolds number based on diameter for the ball is 1100, where the quadratic force law should apply, while the maximum value based on the diameter of a wire is about 6, where the linear force law should prevail.

Since the damping force is neither linear nor quadratic, but rather a combination of the two, it makes sense to establish a damping function which contains both effects simultaneously. Therefore, the pendulum equation becomes

\[ \ddot{\theta} + \alpha \,\dot{\theta} + \epsilon \,\mbox{sign} \left( \dot{\theta} \right) + \beta \left\vert \dot{\theta} \right\vert \dot{\theta} + \omega_0^2 \sin\theta =0 , \]

where the linear damping coefficient \( \alpha = \kappa /m , \) describes air resistance due to the wire, the quadratic damping coefficient β is due to air drag on the pendulum bob, and the third damping term \( \quad \epsilon = c\ell /(2m) \) is necessary for taking into count the bearing, which is subject to dry friction (Coulomb damping). Here \( \quad \omega_0 = \left( g/\ell \right)^{1/2} ,\) and \( \mbox{sign}(x) = \begin{cases} 1, & \ x>0, \\ -1, & \ x<0. \end{cases} \)

Analysis of the experimental data gives the following values of the parameters (Robert A. Nelson and M.G. Olsson, "The pendulum---rich physics from a simple system," American Journal of Physics, Vol. 54, No 2, 112--121, 1986):

\begin{eqnarray*} \alpha &=& 0.012 \pm 0.005 \,\mbox{s}^{-1} , \\ \beta &=& 0.0291 \pm 0.0064 , \\ \epsilon &=& 0.0017 \pm 0.0009 \,\mbox{s}^{-1} . \end{eqnarray*}

It is significant that the effect of air drag is apparent in both the parameters α and β. If air drag could be described purely in terms of the velocity squared, it should affect only the parameter β. If one attemps to fit the data with a damping law based on a single power of the velocity, the power would have to be somewhat less than 2.

In order to find out the relationship between the angle of the pendulum and time t, a good way is to plot θ against t. In order to make the plot, first solve the differential equation with the command NDSolve.

This can be done by assigning constant values to α, ε and ω when using the NDSolve command, getting three different functions in respect to three different α values, and using the Plot command to plot the three functions in one graph

numsol1 =
  NDSolve[{y''[x] == -10*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsol2 =
  NDSolve[{y''[x] == -1*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsol3 =
  NDSolve[{y''[x] == -0.1*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
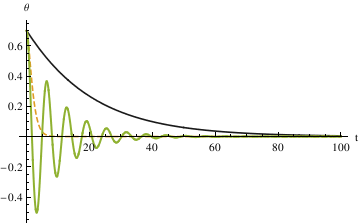
Plot[Evaluate[y[x] /. {numsol1, numsol2, numsol3}], {x, 0, 100}, PlotRange -> All, PlotStyle -> {GrayLevel[0.1], Dashed, Thick}, AxesLabel -> {"t", "\[Theta]"}, PlotLegends -> {"\[Alpha]=10", "\[Alpha]=1", "\[Alpha]=0.1"}]

Another method is to set up a function that takes θ0, ω0, α, ε and tmax as inputs and outputs for a function of θ

DampedDrivenPendulumFunction2[{\[Theta]0_, \[Omega]0_}, \[Alpha]_, \ \[Epsilon]_, tmax_] :=
Module[{\[Theta]}, \[Theta] /. First[ NDSolve[{ \[Theta]''[t] == -Sin[\[Theta][t]] - 2 \[Alpha] \[Theta]'[ t] - \[Epsilon] Sign[\[Theta]'[t]] (\[Theta]'[t])^2, \[Theta][0] == \[Theta]0, \[Theta]'[0] == \[Omega]0}, \[Theta], {t, 0, tmax}
Plot[{DampedDrivenPendulumFunction2[{0.7, 0}, 0.1, 0, 100][x], DampedDrivenPendulumFunction2[{0.7, 0}, 1, 0, 100][x], DampedDrivenPendulumFunction2[{0.7, 0}, 10, 0, 100][x]}, {x, 0, 100}, PlotLegends -> "Expressions", PlotRange -> Full, PlotStyle -> {Thick, Automatic, Dashed}, AspectRatio -> 1.0]
The third method presented here is very different from the first and the second: we create a loop to add solutions into a list.
\[Epsilon] = 0; g = 9.8; \[Omega]0 = 1;
listofsolutions = {};
listofvaluesforalpha = {.1, 1, 10};
Numerically solve the corresponding second order differential equation, leaving alpha as a variable:
pendulumeq = \[Theta]''[t] + 2*\[Alpha] \[Theta]'[ t] + \[Epsilon] Sign[\[Theta]'[ t]]*((\[Theta]'[t])^2) + (\[Omega]0^2)*Sin[\[Theta][t]] == 0;
Get distinct equations for the different values of \[Alpha] and add them to the listofsolutions:
counter = 1;
While[counter <= Length[listofvaluesforalpha], AppendTo[listofsolutions, NDSolve[{Evaluate[ pendulumeq /. {\[Alpha] -> listofvaluesforalpha[[counter]]}], \[Theta][ 0] == .7, \[Theta]'[0] == 0}, \[Theta][t], {t, 0, 100}]]; counter++]
Plot[Evaluate[theta[t] /. listofsolutions], {t, 0, 50}, PlotRange -> All]

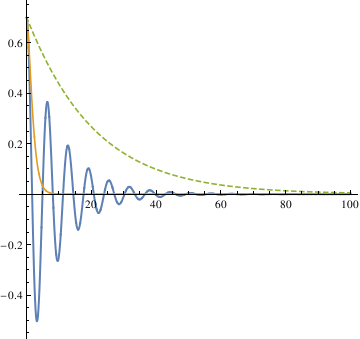
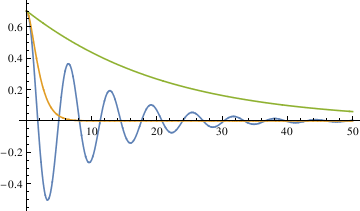
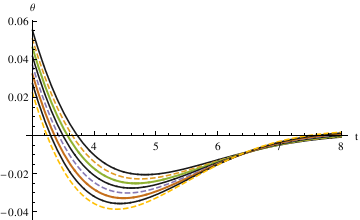
The three different methods all get the same result, from which we can see that the largest damping coefficient does not stop the pendulum the fastest. So the qualitative difference among the three different coefficients is that when α is 0.1, the pendulum oscillates (crosses 0). In other cases, the pendulum does not oscillate (does not cross 0).

The critical damping value is the damping coefficient that stops the pendulum the fastest.

In order to find out the critical damping value of alpha, first we need to define the stop interval, because the pendulum will end up always being in very small oscillation.

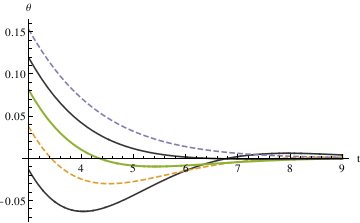
The first method defined - 0.035 < θ < 0.035 as the stop interval. By plotting different functions of θ with different alpha values (0.6, 0.7, 0.8, 0.9, 1.0) in one graph, you can see that α = 0.7 starts to be in the range [-0.035, 0.035] the fastest.

numsola1 =
  NDSolve[{y''[x] == -0.6*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolb1 =
  NDSolve[{y''[x] == -0.7*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolc1 =
  NDSolve[{y''[x] == -0.8*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsold1 =
  NDSolve[{y''[x] == -0.9*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolf1 =
  NDSolve[{y''[x] == -1.0*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
Plot[Evaluate[ y[x] /. {numsola1, numsolb1, numsolc1, numsold1, numsolf1}], {x, 3, 9}, PlotStyle -> {GrayLevel[0.2], Dashed, Thick}, PlotRange -> All, AxesLabel -> {"t", "\[Theta]"}, PlotLegends -> {"\[Alpha]=0.6", "\[Alpha]=0.7", "\[Alpha]=0.8", "\[Alpha]=0.9", "\[Alpha]=1.0"}]
To find out more accurate value of α, plot several different α values close to 0.7:
numsola =
  NDSolve[{y''[x] == -0.74*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolb =
  NDSolve[{y''[x] == -0.73*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolc =
  NDSolve[{y''[x] == -0.72*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsold =
  NDSolve[{y''[x] == -0.71*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolf =
  NDSolve[{y''[x] == -0.70*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolg =
  NDSolve[{y''[x] == -0.69*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsolh =
  NDSolve[{y''[x] == -0.68*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
numsoli =
  NDSolve[{y''[x] == -0.67*2*y'[x] - Sin[y[x]], y[0] == 0.7, y'[0] == 0}, y[x], {x, 0, 1000}]
Plot[Evaluate[ y[x] /. {numsola, numsolb, numsolc, numsold, numsolf, numsolg, numsolh, numsoli}], {x, 3, 8}, PlotStyle -> {GrayLevel[0.1], Dashed, Thick}, PlotRange -> All, AxesLabel -> {"t", "\[Theta]"}, PlotLegends -> {"\[Alpha]=0.74", "\[Alpha]=0.73", "\[Alpha]=0.72", "\[Alpha]=0.71", "\[Alpha]=0.70", "\[Alpha]=0.69", "\[Alpha]=0.68", "\[Alpha]=0.67"}]
Then α = 0.69 should roughly be the critical damping value.
Pi/2*0.005
Out[25]= 0.00785398
findmid[x_, y_] := (x + y)/2
Plot[{DampedDrivenPendulumFunction2[{0.7, 0}, 1, 0, 100][x], DampedDrivenPendulumFunction2[{0.7, 0}, 0.7, 0, 100][x]}, {x, 0, 30}, PlotLegends -> "Expressions", PlotRange -> {-0.007853981633974483`, 0.007853981633974483`}, PlotStyle -> {Thick, Automatic, Dashed}, AspectRatio -> 1.0]
From this graph, when α = 1, the pendulum settles in the stop range faster than when α = 0.7. This means that 0.7 is too small, and 1 may be too large. Then try the mid-value 0.75.
findmid[1, 0.7]
Plot[{DampedDrivenPendulumFunction2[{0.7, 0}, 0.85, 0, 100][x], DampedDrivenPendulumFunction2[{0.7, 0}, 1, 2, 100][x], DampedDrivenPendulumFunction2[{0.7, 0}, 0.7, 0, 100][x]}, {x, 0, 30}, PlotLegends -> "Expressions", PlotRange -> {-0.007853981633974483`, 0.007853981633974483`}, PlotStyle -> {Thick, Automatic, Dashed}, AspectRatio -> 1.0]

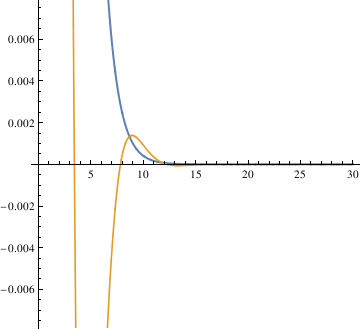
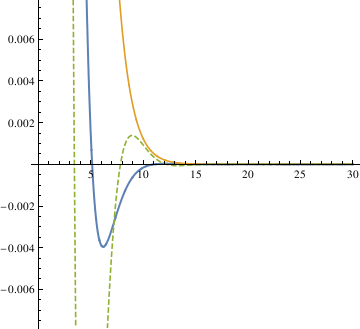
When α = 0.85, the pendulum settles in the range faster than when α = 1. So the critical value may be smaller than 0.85. Try the mid value of 0.85 and 0.7. Finally, the answer yielded from this method is 0.81.

The third method defines the stop interval as not passing 0 in the time span 0 < t \ < 500, uses a function piano to check if the pendulum oscillates.

\[CurlyEpsilon] = 0; g = 9.8;
\[CapitalOmega]0 = 1;
listofsolutions = {};
listofvaluesfor\[Alpha] = Range[0, 2, .0005];
pendulumeq = \[Theta]''[t] + 2*\[Alpha]*\[Theta]'[t] + \[CurlyEpsilon]* Sign[\[Theta]'[t]]*((\[Theta]'[t])^2) + (\[CapitalOmega]0^2)* Sin[\[Theta][t]] == 0;
counter = 1;
While[counter <= Length[listofvaluesfor\[Alpha]], AppendTo[listofsolutions, NDSolve[{Evaluate[ pendulumeq /. {\[Alpha] -> listofvaluesfor\[Alpha][[counter]]}], \[Theta][ 0] == .7, \[Theta]'[0] == 0}, \[Theta][t], {t, 0, 1000}]]; counter++];
evaluatedlistofsolutions = Evaluate[\[Theta][t] /. listofsolutions];
piano is a function that checks to see if the pendulum ever swings past θ = 0 for each of the functions in the list. If the answer is no, then it means that the pendulum no longer oscillates for that value of α.
piano[key_] :=
  Catch[If[FindMinValue[ evaluatedlistofsolutions[[key]], {t, 0, 500}] > 0, Throw[key], Throw[906]]];
counter2 = 1;
While[piano[counter2] == 906, counter2++];
Print["The Value of \[Alpha] at which the function \[Theta][t] stops \ oscillating is ", listofvaluesfor\[Alpha][[counter2]]]
The Value of α at which the function θ[t] stops oscillating is 0.8985
Plot[evaluatedlistofsolutions[[piano[counter2]]], {t, 0, 20}, PlotRange -> All]
Now we assume that α is not zero.
DampedDrivenPendulumFunction2[{\[Theta]0_, \[Omega]0_}, \[Alpha]_, \ \[Epsilon]_, tmax_] :=
  Module[{\[Theta]}, \[Theta] /. First[ NDSolve[{ \[Theta]''[t] == -Sin[\[Theta][t]] - 2 \[Alpha] \[Theta]'[ t] - \[Epsilon] Sign[\[Theta]'[t]] (\[Theta]'[t])^2, \[Theta][0] == \[Theta]0, \[Theta]'[0] == \[Omega]0}, \[Theta], {t, 0, tmax}] ]]
g5 = DampedDrivenPendulumFunction2[{0.7, 0}, 0.1, 1, 100]
g6 = DampedDrivenPendulumFunction2[{0.7, 0}, 10, 1, 100]
g7 = DampedDrivenPendulumFunction2[{0.7, 0}, 1, 1, 100]
Plot[{g5[x], g6[x], g7[x]}, {x, 0, 100}, PlotLegends -> "Expressions", PlotRange -> Full, PlotStyle -> {Thick, Automatic, Dashed}]
When ε is 1, the qualitative difference among different alpha when α is 1, 0.1, or 10 is the same. But when α is 0.1, it oscillates with less times compared to the case when ε is 0.

 

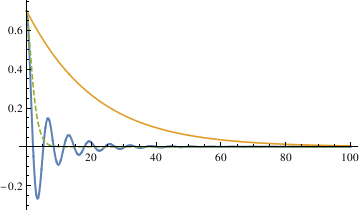
III. A Real Pendulum

 A real pendulum bob has a finite size and the suspension wire has a mass. In addition, the wire connections to the bob and the support may have some structure. Normally, pendulum osccilations take place in air. All such effects should be taking into account in physical pendulum equation.

 By Archimedes's principle, the apparent weight of the bob is reduced by the weight of the displaced air. This property has the effect of increasing the period since the effective gravity is decresing. The kinetic energy of the system is partly effected by the air by adding mass to the bob's inertia (but not weight) proportional to the mass of the displaced air. The need for the added mass correction was noted by Friedrich Bessel (1784--1846) in 1828. (It was discovered independently by Pierre Du Buat (1734--1809) in 1786, but only Bessel's work attracted attention to his result.) The dependence of added mass on viscosity was derived by George Stokes (1819--1903) in 1859.

 The length of the pendulum is incresed by stretching of the wire due to the weight of the bob. The effective spring constant for a wire of rest length \( \ell_0 \) is

\[ k = ES/ \ell_0 , \]
where E is the elastic modulus (also known as Young's modulus, which is a number that measures an object or substance's resistance to being deformed elastically), which is defined as the slope of its stress–strain curve in the elastic deformation region, and S is the cross-sectional area. For steel, \( E 2.0 \times 10^{11} \) Pa.

 There is also dynamic stretching of teh wire from the apparent centrifugal and Coriolis forces acting on the bob during mortion. The corresponding mathematical model leads to a system of differential equations, which is a topic of the second course. See M.G. Olson, American Journal of Physics, Vol. 44, 1211, 1976.

 

IV. Driven Pendulum

A driven pendulum may exhibit a chaotic motion. It consists of a mass m fixed at a distance \( \ell \) from a pivot which is subject to a vertical oscillation \( y = A\, \cos \left( \omega \, t \right) . \) Let θ be the angular coordinate of m measured counterclockwise from the down position, and \( \phi = \pi - \theta \) the complementary displacement measured clockwise from the up orientation. The kinetic and potential energies are

 

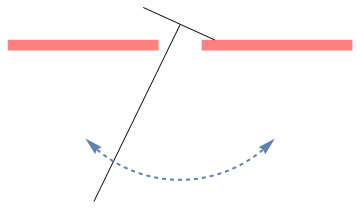
V. Rocking Rigid Pendulum

plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{-2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{-0.85, 1.0}, {0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
makeArrowPlot[g_Graphics, ah_: 0.05, dx_: 1*^-6, dy_: 1*^-6] :=
Module[{pr = PlotRange /. Options[g, PlotRange], gg, lhs, rhs},
gg = g /. GraphicsComplex -> (Normal[GraphicsComplex[##]] &);
lhs := Or @@
Flatten[{Thread[Abs[#[[1, 1, 1]] - pr[[1]]] < dx], Thread[Abs[#[[1, 1, 2]] - pr[[2]]] < dy]}] &;
rhs := Or @@ Flatten[{Thread[Abs[#[[1, -1, 1]] - pr[[1]]] < dx], Thread[Abs[#[[1, -1, 2]] - pr[[2]]] < dy]}] &;
gg = gg /.
x_Line?(lhs[#] && rhs[#] &) :> {Arrowheads[{-ah, ah}], Arrow @@ x};
gg = gg /. x_Line?lhs :> {Arrowheads[{-ah, 0}], Arrow @@ x};
gg = gg /. x_Line?rhs :> {Arrowheads[{0, ah}], Arrow @@ x};
gg]
curve = Plot[{-Sqrt[9 - x^2]}, {x, -2.2, 2.2}, PlotStyle -> {Thick, Dashed}, Axes -> False] // makeArrowPlot
Show[a, line1, line2, curve]

Figure 1: Rocking rigid pendulum.

A rigid pendulum, such as a long rod, has a short cross-bar rigidly attached to it. As it oscillates in vertical plane, it is supported on ends of the cross-bar as they alternately contact a fixed horizontal surface:
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
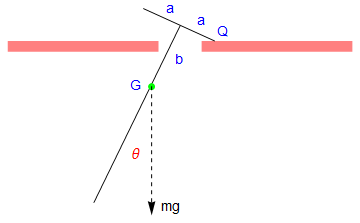
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{-2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{-0.85, 1.0}, {0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
p2 = Graphics[{Dashed, Arrow[{{-0.66, -0.8}, {-0.66, -3.8}}]}]
point = Graphics[{PointSize[Large], Green, Point[{-0.66, -0.8
t1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Red], {-1.0, -2.4}]]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {-1.0, -0.8}]]
a1 = Graphics[Text[Style["a", FontSize -> 14, Blue], {0.5, 0.7}]]
a2 = Graphics[Text[Style["a", FontSize -> 14, Blue], {-0.2, 1.0}]]
Q = Graphics[Text[Style["Q", FontSize -> 14, Blue], {1.0, 0.45}]]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {0.0, -0.2}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {-0.2, -3.6}]]
Show[a, line1, line2, point, p2, t1, t2, a1, a2, Q, b, mg]
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
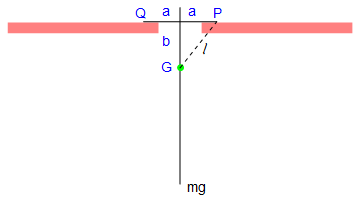
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{2, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{0.85, 1.0}, {-0.8, 0.25}}], PlotRange -> {{-2, 2}, {-4, 1}}]
p2 = Graphics[{Dashed, Arrow[{{0.66, -0.8}, {0.66, -3.8}}]}]
point = Graphics[{PointSize[Large], Green, Point[{0.66, -0.8}]}]
t1 = Graphics[ Text[Style["\[Theta]", FontSize -> 14, Red], {1.0, -2.4}]]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {0.3, -0.8}]]
P = Graphics[Text[Style["P", FontSize -> 14, Blue], {-0.9, 0.45}]]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {0.0, -0.2}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {0.22, -3.6}]]
Show[a, line1, line2, point, p2, t1, t2, P, b, mg]
plus = Polygon[{{-1/2, 0}, {-1/2, 1/4}, {-4, 1/4}, {-4, 0}}]
minus = Polygon[{{1/2, 0}, {1/2, 1/4}, {4, 1/4}, {4, 0}}]
a = Show[Graphics[{Pink, minus}], Graphics[{Pink, plus}]]
line1 = Graphics[Line[{{0, -3.5}, {0, 0.6}}], PlotRange -> {{-2, 2}, {-4, 1}}]
line2 = Graphics[Line[{{0.85, 0.27}, {-0.85, 0.27}}], PlotRange -> {{-2, 2}, {-4, 1}}]
P = Graphics[Text[Style["P", FontSize -> 14, Blue], {0.9, 0.45}]]
Q = Graphics[Text[Style["Q", FontSize -> 14, Blue], {-0.9, 0.45}]]
mg = Graphics[Text[Style["mg", FontSize -> 14, Black], {0.4, -3.6}]]
point = Graphics[{PointSize[Large], Green, Point[{0, -0.8}]}]
t2 = Graphics[Text[Style["G", FontSize -> 14, Blue], {-0.3, -0.8}]]
p3 = Graphics[{Dashed, Line[{{0, -0.8}, {0.85, 0.27}}]}]
b = Graphics[Text[Style["b", FontSize -> 14, Blue], {-0.3, -0.2}]]
a1 = Graphics[Text[Style["a", FontSize -> 14, Blue], {0.3, 0.5}]]
a2 = Graphics[Text[Style["a", FontSize -> 14, Blue], {-0.3, 0.5}]]
ell = ToExpression["\ell", TeXForm]
t3 = Graphics[Text[Style[ell, FontSize -> 14, Black], {0.6, -0.4}]]
Show[a, line1, line2, point, p3, t2, a1, a2, P, Q, b, mg, t3]
     

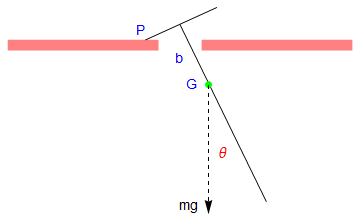Let the mass of the pendulum be m, and the length of the attached bar be 2 a. Since the construction of the rigid pendulum is symmetric, the center of gyration, which we denote by G, is along the main rod. Let k be the radius of gyration of the pendulum about G, so that the square of its radius of gyration about P and Q is \( k^2 + \ell^2 . \)

 

The first half-cycle of the motion

Suppose that the pendulum is set in motion from the central position with initial conditions

\[ \theta =0 \quad \mbox{and} \quad \dot{\theta} = \omega_1 \qquad\mbox{at} \quad t=0. \]
Since energy is assumed to be conservative, the total energy is a constant:
\[ \frac{1}{2}\, m \left( k^2 + \ell^2 \right) \dot{\theta}^2 + mg \left( a\,\sin \theta -b\,\cos \theta \right) = \mbox{constant} . \]
For small oscillations, powers of θ higher than the first may be neglected, yielding
\[ \left( k^2 + \ell^2 \right) \dot{\theta}^2 + 2ag \,\theta = \mbox{constant} \qquad\mbox{or} \qquad \dot{\theta}^2 + c^2 \theta = \mbox{constant} , \]
where \( c^2 = 2ga \left( k^2 + \ell^2 \right) . \) The initial conditions enable this to be written as
\[ \dot{\theta}^2 + c^2 \theta = \omega_1^2 , \]
When the pendulum first comes to rest, let
\[ t= \frac{1}{2}\,\tau_1 , \quad \theta = \theta_1 , \quad \dot{\theta} =0. \]
Then
\[ \dot{\theta}^2 + c^2 \theta = \omega_1^2 \qquad\Longrightarrow \qquad \theta_1 = \omega_1^2 / c^2 ., \]
Now
\begin{align*} \frac{1}{2}\,\tau_1 &= \int_0^{\theta_1} \, \frac{{\text d} \theta}{\dot{\theta}} = \int_0^{\theta_1} \, \frac{{\text d} \theta}{\sqrt{\omega_1^2 - c^2 \theta}} = \frac{2}{c^2} \left[ \sqrt{\omega_1^2 - c^2 \theta} \right]_{0}^{\theta_1} \\ &= \frac{2\omega_1}{c^2} = \frac{2\sqrt{\theta_1}}{c} . \end{align*}
Clearly, the time taken for θ to reach zero again will also be \( \frac{1}{2}\,\tau_1 , \) and the angular speed will then be ω1 again. Thus, the first "half period" of oscillation will be \( \tau_1 = 4 \sqrt{\theta_1} /c . \)

 

The first transition through the central position

 

 

 

Return to Mathematica page

Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)