Preface
This web site provides an introduction to the computer algebra system Maple, created by MapleSoft ©. This tutorial is made solely for the purpose of education, and intended for students taking APMA 0330 (Methods of Applied Mathematics - I) course at Brown University. The tutorial accompanies the textbook Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043
Maple is a computer algebra system (CAS for short) that is able to give exact solutions in an analytic form to numerous problems related to differential equations. In addition to symbolic computation packages, Maple incorporate many numerical algorithms for approximating solutions to problems that do not admit exact solutions. It also contains graphic programs allowing visualization of information and results.
Maple is structured on two levels. the basic level, the 'kernel', of about 10%, contains primitive and fundamental commands, and algorithms for arithmetic and polynomial calculus. The higher level, maple's library, of about 90%, contains maple code that can be called on commands, and numerous specialized packages, such as LinearAldebra or DEtools.
Maple is a large, complex computer algebra system, only part of which is introduced in this tutorial. If you have not taken or are not taking a course regarding Maple or programming, such as CSCI 0150 (Introduction to Object-Oriented Programming and Computer Science) or ENGN 0030 (Introduction to Engineering), then please begin from Chapter 1. Otherwise, please proceed with this Introduction. For those who have used Maple before, please note that there are certain commands and sequences of input that is specific to solving differential equations, so it is best to read through this tutorial in its entirety. This tutorial is based on latest version of Maple, but some pages are not updated. Therefore, tutorials from other sources may or may not be compatible with this tutorial.
The commands in this tutorial are all written in red text (as Maple input), while Maple output is in blue, which means that the output is in 2D output style. You can copy and paste all commands into Maple, change the parameters and run them. You, as the user, are free to use the mw files and scripts to your needs, and have the rights to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. The tutorial accompanies the textbook Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043. Any comments and/or contributions for this tutorial are welcome; you can send your remarks to <Vladimir_Dobrushkin@brown.edu>
0.1. Introduction
When opening the application you will be directed to the start screen
Explaination of Toolbar Icons (from Maplesoft.com):
There are some options that depend on which tool you are using in the second row of Toolbar Icons (from Maplesoft.com)
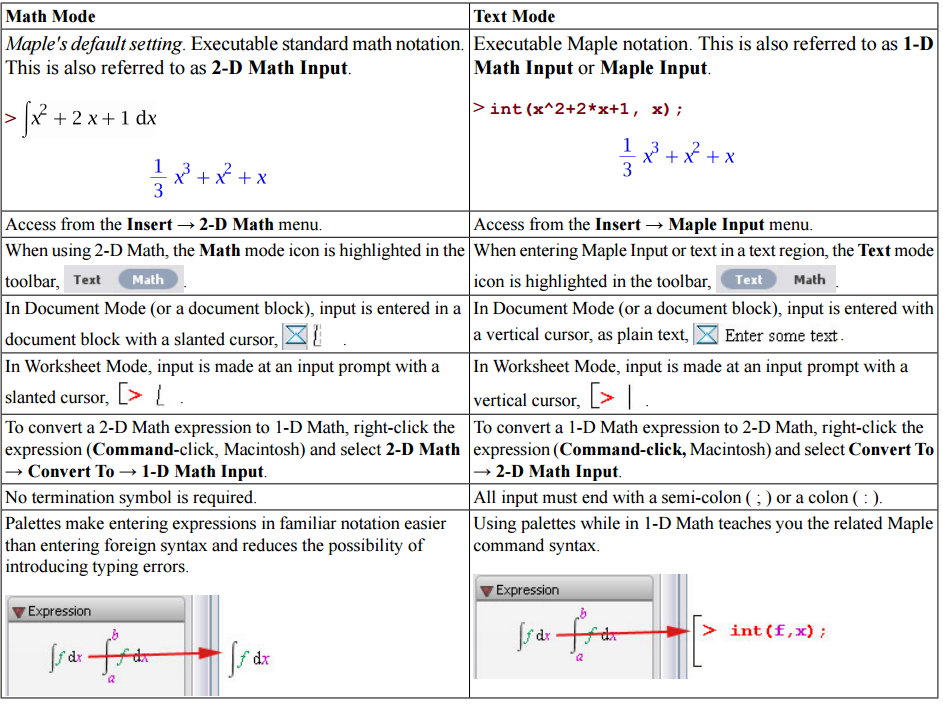
The most useful to use in APMA 33/34 will be Text and Math. Here is a quick comparison between the two so the basics are understood (from Maplesoft.com):
On the left side of your screen are where the Palletes are located.
"Palettes are collections of related items that you can insert into a document by clicking or drag-and-dropping.
By default, palettes are displayed in the left pane of the Maple environment when you launch Maple. If the palettes
are not displayed,
1. From the View menu, select Palettes.
2. Select Expand Docks.
3. Right-click (Control-click, Macintosh) the palette dock. From the context menu, select Show All Palettes.
Alternatively, from the main menu, select View ? Palettes ? Arrange Palettes to display specific palettes.
You can create a Favorites palette of the expressions and entities you use often by right-clicking (Control-click,
Macintosh) the palette template you want to add and selecting Add To Favorites Palette from the context menu." (Maplesoft.com)
To open another window create a new file and you will see "Untitled" next to "Start.mw" under the first toolbar. Click the name of your files to switch betwen them.
In Maple, mathematical expressions are typed directly after Maple prompt, which can be either sland (/) or right carrot (>), depending on the input specification. We drop writing a Maple prompt to simplify copying and pasting corresponding scripts. In the previous versions of Maple, the semicolomn (;) was required to indicate the end of input command. In the latest versions it is redundant. Throughout Tutorial, we present Maple commands in red color (as Maple input), while Maple output is in blue, which means that the output is in 2D output style. To switch your input into Maple input, type Ctrl-M or use options Maple Input/monocpaced in math mode or Maple input, depending on Maple's version. Everything that is typed after # is ignored by Maple. This tutorial will be completed in the default Mathsheet Mode -- 2D Math. Therefore, any Maple prompt is ignored and all commands are typed in red plain text.
0.0.1. Arithmetic Operationss
The symbols +, -, *, /, and ^ (or **) denote addition, subtraction, multiplication, division, and exponentiation (4^2 = 4**2 = 16). When a string of operations are specified in a command, MAPLE first does exponentiations, then multiplications and divisions, then additions and subtractions. To change the order, use parentheses. Editing commands. If you make a mistake in a command (like forgetting a semicolon) or want to change a command, you can go back and edit the command with the cursor and mouse as you would a word-processor text. Operating on the last result. Use a percentage character (%) to refer to the result of the last calculation, and a double percentage character (%%) to refer to the next-to-last result. For example,
5*2;
10
7 + %;
17
%*%% 170
Exact arithmetic and floating-point arithmetic MAPLE calculates fractions (exact arithmetic) unless you specify that you want decimals (floating-point arithmetic) with the evalf function ("evalf" stands for "evaluate using floating-point arithmetic"):
25/27 + 3/51;
evalf(%)
0.9847494553
To specifies number of digits, type
evalf[25](%)
Using evalf or Digits affects the number digits used to perform the floating-point computations.
You can get help with MAPLE syntax by using the HELP menu, as described previously. If you have a question about a particular command, you can quickly get help by typing a question mark followed by the command name (no semicolon). For example,
? evalf
will open a window containing information about what the evalf function does and how to use it.
Close the help window. Click on the little box at the upper left of the window and select Close.
0.1.2. Algebraic Operations/variables/constants
This section of the tutorial will be compltered in Math environment -- 2D Math.
Try the following input (Type in exactly as you see it. Do not include the left carrot >, as this is only for showing Maple input in forms of text other than in Maple):
> |(x^3+x+sqrt(x))/(Pi*x-1)|; # comments are typed here
The resulting output should be:
Greek Letters
To insert a Greek letter into Maple, type the name of the letter, for example gamma, and then hit
the escape key. Uppercase Greek letters can be inserted by making the first letter of your text
uppercase, for example Gamma. Sometimes the escape key will bring up a menu that will allow
you to choose between several different options.
Subscripts
Using subscripts in Maple to differentiate between variables can be extremely useful. To insert
a subscript, type an underscore ( _ ). When you are done, press the right arrow key to get back
to normal input. This notation is not perfect. If you are using a variable with a subscript, don’t
assign a value the variable alone. For example if you are using x1 and x2, don’t assign anything
to just x. Doing so will generate recursive expression error messages or cause your code not to
function properly.
Clearing Variables
The restart command will clear all variables and all packages:
> restart
Variables can also be cleared manually. To do this we reassign the variable to its own name
within single quotations.
> x:=10
> 5*x+15
> x:='x'
> 5*x+15
Semicolons
In older versions of Maple, every command line had to end with a semicolon. This is no longer
the case in Maple 14 or later versions. However, semicolons can still be used to run multiple expressions on the
same line. This is sometimes useful for defining variables. If you make a mistake in a command (like forgetting a semicolon) or want to change a command, you can go back and edit the command with the cursor and mouse as you would a word-processor text.
0.1.3. Constants and Packages
In Maple, the constant Pi is the irrational number 3.1415...; it is denoted by Pi, not by pi (\( \pi \) ) neither by PI (\( \Pi ,\) ) which is upper case Greek letter.
Many commands are grouped together in packages. You can type the long name, or enter a with () command prior to using a command from the particular package.E.g. Linear Algebra[ Determinant ] ( M ) / with(Linear Algebra) : Determinant( M )
Exponential Function
In Maple, e is just a variable. To use e you must use either use the Expression Pallete to call e or use exp(x)
Euler's Totient Function
First type
with(numtheory)
then use the calling sequence:phi(n) where n is an integer
Fibonacci
with(combinat):
Call sequence: fibonacci(n) where n is an integer. Computes the nth Fibonacci number F(n).
For a sequence of Fibonacci numbers, say the 0-10th, type
seq(fibonacci(i),i=0..10)
Bernoulli
Call sequence: bernoulli(n) where n -nonnegint; the index of the required Bernoulli number or polynomial
Stirling Number
Call sequence: Stirling1(n,m) where m and n are positive intergers
May have to type the next line after you already called the call sequence
=convert(,Sum)
Euler Numbers
Call Sequence: euler(n,x) where n is a non-negative integer and x is an expression
The function euler computes the nth Euler number, or the nth Euler polynomial in x
There are a few things to note when defining mathematical expressions:
- Types of operations are expressed as + (addition), - (subtraction), *(multiplication), / (division).
- Exponents are expressed with carrots ^. Beware that when you input exponents, you must hit the right arrow key afterwards or else you will continue to type into the exponent. The same concept applies to division; when you are typing in the numerator/denominator, in order to move the blinking cursor outside of the fraction, you must hit the arrow keys to move it outside of the fraction (Clicking works as well).
- Type math first and then press [Enter] to see the result. And the result will show on the nest line.
- Type math first and then press [Ctrl][=] and then the result will show on the same line as the math you typed.
- Asking further questions: place your cursor on the result and then the context menu will offer several further operations such as integration and derivative.
- You can always go back to the calculations you entered and change the numbers to get new results.
- Maple has over 1000 palette symbols to input data.
- You can use the Handwriting palette to find the symbol you want.
- You can type in the first few characters of the symbol and then press [Ctrl][Space] to choose the symbol you want from the list.
- To multiply two variables, a space has to be inserted. “a b” means a times b, while ‘ab’ means a variable whose name is ‘ab’.
- Maple understands mathematical notation such as y’ (y prime).
- Absolute values are expressed with vertical lines ||. They can also be expressed using the abs( ) command.
- Square roots (radicals) are expressed with the input sqrt( ).
- The percent sign ( % ) can be used as shorthand for the most recent output.
- When inputting π, you must type in Pi. Maple will not accept pi as π.
- When using division, be sure to separate the numerators and denominators with parentheses to prevent errors.
- In new versions of Maple, typing semicolumn (;) at the end of mathematical expression is not needed.
- When you wish to substitute a variable with a value, use the subs command. The generic syntax is as follows:
subs(value, equation); Therefore, if we use the above equation to substitute x with the value -2, we have:
subs(x=-2, %) 10
For more complicated equations where after substitution you still have an equation, remember you can use evalf(%)
- The % is a special symbol which takes in the most recently inputted equation. This is a useful symbol to use to avoid assigning equations to variables.
- You will notice in #7 that the resulting output will not be a
specific value, but another equation with the x substituted with -2.
Therefore, you may use the evalf command to receive a specific answer.
The syntax is straightforward and simple, you just have to input the
equation back in.
evalf(%);
1.386687900If you want to see more digits, say 25, type evalf[25](%); or
evalf(%, 25) - Maple has two commands to calculate derivatives. The symbolic notation is D, and old fashion notation is diff:
> f:=x->x^3;
> D(f)(x);
> D(x^3);
> diff(f(x),x);
> diff(x^3,$2);
In Maple, defining functions is done by the command “:=”, followed by expression involving independent variable, which is x in our case. When you type, do not include the right carrot >, as this is only for showing Maple input in forms of text other than in Maple:
> f:=x->x^3+x+sqrt(x);
Note that the square root sqrt(x) can be defined as x^(1/2) or x^(0.5); however, it will slow down all numerical computations because Maple uses logarithm for its representation and the corresponding calculations are based on different algorithm.
0.1.4. Substitution
The command
> g:=unapply(f,x);
configures the expression f as a function of x. This has two effects.
(i) It enables you to call for the value of f at a particular value of x. For example g(a) will then be the expression f with x replaced by a. This is obviously useful in imposing boundary conditions.
(ii) It ensures that Maple will treat all other parameters in f as being independent of x. You will find this useful if at any point you get output including derivatives of quantities you want to treat as constants.
4. Another way of obtaining the expression f with x replaced by a is to use the `subs' command:-
> g:=subs(x=a,f);
More than one substitution can be made at the same time, for example
> g:=subs({x=a,y=b},f);
Notice that the separate substitutions are separated by commas and the complete set is then enclosed in {....}.
Once you have given a value to an expression (e.g. x=a , Maple will assume that value for all subsequent calculations, including new runs of the code. If you want to change such an assignment, you will need to issue the command
> restart;
which essentially erases the effect of all previous calculations.

