Part I: Plotting

---

This tutorial contains many Mathematica scripts. You, as the user, are free to use all codes for your needs, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. I would like to extend my gratitude to all of the students that aided me in developing this tutorial. The coding, testing, and debugging required a concerted effort, and the following students deserve recognition for their input: Emmet and Jesse Golden-Marx (Fall 2011), Pawel Golyski (Fall 2012). Any comments and/or contributions for this tutorial are welcome; you can send your remarks to <Vladimir_Dobrushkin@brown.edu>

1.1. Plotting functions

---

One of the best characteristics of Mathematica is its plotting ability. It is very easy to plot a variety of functions using Mathematica. For a plot, it is necessary to define the independent variable that you are graphing with respect to. Mathematica automatically adjusts the range over which you are graphing the function.

In the above code, we use a natural domain for the independent variable to be \( [0,2\pi ] .\) In general, the domain of the independent variable is usually chosen based on a particular interest; one may try different options before obtaining a desired figure.
In this command sequence, the independent variable is x and the range is 0 to \( 2\pi .\) For Plot, after entering the function that you wish to graph, you separate the equation and add {independent variable, lower bound, upper bound}.
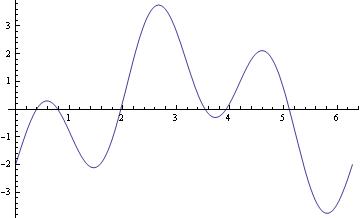
This is a simple Plot command. In this example, we are just plotting a function using Mathematica default capabilities, but it is possible to specify the range with PlotRange command. The above graph can also be obtained with the following script: To place a text inside a figure, Mathematica has a special command Text[expr, coordinates, offset] that specifies an offset for the block of text relative to the coordinate given. Providing an offset { dx, dy } specifies that the point ( x, y ) should lie at relative coordinates { dx, dy } within the bounding rectangle that encloses the text. We demonstrate it with the following codes: However, when we change dimensions of the graph, the text is displayed differently. The following table of graphs can be displayed using GraphicsGrid command. GraphicsGrid by default puts a narrow border around each of the plots in the array it gives. You can change the size of this border by setting the option Spacings -> { h, v} . The parameters h and v give the horizontal and vertical spacings to be used. The Spacings option uses the width and height of characters in the default font to scale the h and v parameters by default, but it is generally more useful in graphics to use Scaled coordinates. Scaled scales widths and heights so that a value of 1 represents the width and height of one element of the grid. How to add text to a graph, see
http://reference.wolfram.com/language/howto/AddTextToAGraphic.html.en
To add test outside the picture, see
http://reference.wolfram.com/language/howto/AddTextOutsideThePlotArea.html.en
The general reference is
http://reference.wolfram.com/language/howto/AddTextToAGraphic.html

On most computer systems, Mathematica can produce not only graphics but also sound. Mathematica treats graphics and sound in a closely analogous way, using command Play. For instance, the previous function can be used to play, on a suitable computer system, a pure tone with a frequency of 440/2π hertz for one second.

For multiple plots, use either command Show or you can use {} with commas. Show can be used to change the options of an existing graphic or to combine multiple graphics.

Show command can be used to adjust the Background option of an existing graphic

A graphic of a function can be made discrete:

We can shift the origin to another point, as the following example shows.

When you need to restrict the vertical range, use PlotRange command as the following example shows.

 

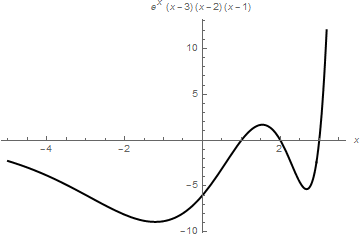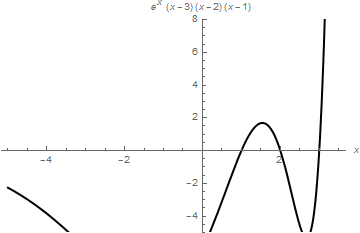Plot sine function downward:

Now plot with arrows, but without units:

Example. Tractrix (from the Latin verb "trahere" -- pull, drag; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a tractor (pulling) point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. By associating the object with a dog, the string with a leash, and the pull along a horizontal line with the dog's master, the curve has the descriptive name hundkurve (dog curve) in German. It is therefore a curve of pursuit. It was first introduced by Claude Perrault (1613 -- 1688) in 1670. Trained as a physician, Claude was invited in 1666 to become a founding member of the French Academie des Sciences, where he earned a reputation as an anatomist. The first known solution was given by Christian Huygens (1692), who also named the curve the tractrix. Its parametric equation is

To plot tractrix curve, we use the following code: