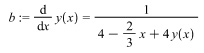First Order Ordinary Differential Equations
This web site provides an introduction to the computer algebra system Maple, created by MapleSoft ©. This
tutorial is made solely for the purpose of education, and intended for students taking APMA 0330 course at Brown University.
The commands in this tutorial are all written in red text (as Maple input), while Maple output is in blue, which means that the output is in 2D output style. You can copy
and paste all commands into Maple, change the parameters and run them. You, as the user, are free to use the mw files and scripts
to your needs, and have the
rights to distribute this tutorial and refer to this tutorial as long as
this tutorial is accredited appropriately. The tutorial accompanies the textbook
Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043.
Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Maple tutorial for the first course APMA0330
Return to Maple tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
The input should generate the above direction field. Unfortunately, you must plot differential equations using dfieldplot explicitly. Therefore, it is best to solve a given differential equation to express it explicitly if it is given implicitly.
The input should generate the above direction/slope field with three curves approaching y(t)=20. Note that the initial values used for the DEplot command can be in the form of an array using brackets. Unfortunately, for DEplot, like dfieldplot, the differential equations must be expressed explicitly.
Deriving analytical solutions in Maple is a cumulative process.
This means that the more specific the answer is that you’re looking for,
the more steps you have to take to derive that answer. In general,
deriving analytical solutions is a two step process, which is solving
for a general solution and then solving for the particular solution.
Analytical solutions are one of the easiest topics to do in Maple,
since Maple will do most of the work for you. All you need to know is
the differential equation and any initial conditions it may have to
obtain the general and particular solution.
In order to find the general solution, first define the ODE, and then use the dsolve command.
For example:
> ode:= diff(y(x),x)=2*y(x)+10;
> dsolve(ode)
As you can see, the _C1 seen in the output of the second command
line represents a constant, which would be normally written as “+C” or "-C."
The equation of y(x) is the general solution to the ODE.
Solving for a particular solution requires the same procedure as
solving for general solutions, except it requires including initial
conditions.First, define the initial conditions, then use the dsolve
command to solve the ODE subject to the initial conditions.
Let’s use the above ODE for this example:
> ics:=y(0)=1;
> dsolve({ode,ics});
I. Solving Using Direction/Slope Fields (dfieldplot)
*Refer to Maple file “Direction Fields”
When solving ODEs, there are many methods in plotting them. In this
section, we will learn how to use three plot commands in the DEtools
package to plot the solutions to ODEs. The dfieldplot command draws out a
direction/slope field of the given function. The generic syntax of the
command is as follows:
> with(DEtools):
> dfieldplot(differential equation, independent variable, x range, y range);
In order to express a differential equation, for example a function
of y in relation to x, you must enter “diff(y(x),x).” In some
tutorials, this can be expressed as “D(y)(x),” but for simplicities
sake, we will use the former expression.
Try out the following:
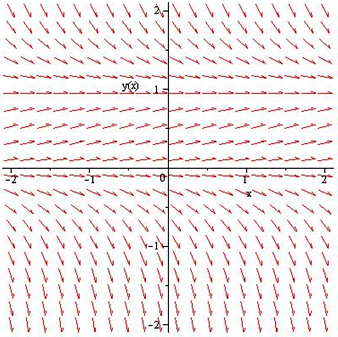
> dfieldplot(diff(y(x),x)=y(x)*(1-y(x)), y(x), x=-2..2, y=-2..2);
The input should generate the above direction field. Unfortunately,
you must plot differential equations using dfieldplot explicitly.
Therefore, it is best to solve a given differential equation to express
it explicitly if it is given implicitly.
*Refer to Maple file “Direction Fields”
If you wish to plot the solutions to the differential equations in a
slope field, you must use the DE plot command. The parameters to enter
are the same as the dfieldplot command, but includes the initial values
and any options.Therefore, the generic syntax of the DEplot command
would be:
> DEplot(differential equation, independent variable, x range, y range, Initial Value(s), Line Color);
Try the following example which involves Newton’s law of cooling:
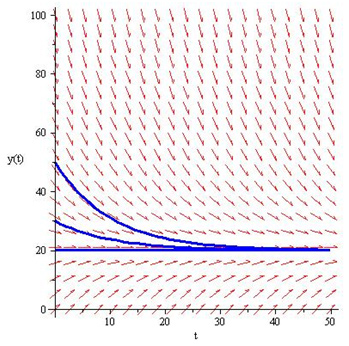
> ode:=diff(y(t),t)=k*(Am-y(t)): Am:=20: k:=0.1:
> ivs := [y(0)=20, y(0)=30, y(0)=50]:
> DEplot(ode,y(t),t=0..50,y=0..100,ivs,linecolor=blue);
The input should generate the above direction/slope field with
three curves approaching y(t)=20. Note that the initial values used for
the DEplot command can be in the form of an array using brackets.
Unfortunately, for DEplot, like dfieldplot, the differential equations
must be expressed explicitly. DEplot has many option to produce nice looking graphs. We give some examples.
eq := diff(y(t), t) = y(t)^3+t:
DEplot(eq, y(t), t = -8 .. 2, [[y(-5) = 1], [y(-3) = 1], [y(0) = 1],
[y(1) = 1]], y = -5 .. 5, title = 'Direction*Field', color = blue,
linecolor = black);
Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution further right of -4.3483781, probably a singularity
Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution further right of -1.9224372, probably a singularity
Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution further right of .47465907, probably a singularity
Warning, plot may be incomplete, the following errors(s) were issued:
cannot evaluate the solution further right of 1.3648127, probably a singularity
Now we add another option:
DEplot(eq, y(t), t = -8 .. 2, [[y(-5) = 1], [y(-3) = 1], [y(0) = 1],
[y(1) = 1]], y = -5 .. 5, title = 'Direction*Field', color = blue,
linecolor = black, arrows = comet, dirfield = 50);
Example.
*Refer to Maple file “Direction Fields”
The odeplot command is slightly different than the DEplot, and is
slightly enhanced compared to the dfieldplot. Compared to other plot
commands, odeplot has the ability to animate the solution to an ODE.
Note that the odeplot command is within the plot package, not the
DEtools package. The generic syntax of the odeplot command is fairly
easy and is as follows:
> odeplot(dsolve({differential equation, initial value}, type=numeric, range)
The dsolve command solves the differential equation. Plotting the
result will give us a graph of the solution to the ODE. The type=numeric
option finds a numerical solution for the differential equation.
Let’s see this in a simple example:
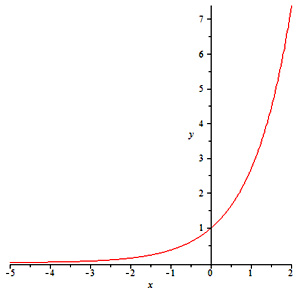
> with(plots) :
> ode :=dsolve({diff(y(x),x)=y(x),y(0)=1},type=numeric, range=-5..2) :
> odeplot(ode);
This should generate the following graph:
A differential equation \( y' = f(x,y) \) is called separable if its slope function \( f(x,y) \) can be represented as a product of two functions, each depending on another variable:
\( f(x,y) = p(x)\,q(y) . \) A differential equation of first order is referred to as an autonoumous if its slope function does not depend on independent variable:
\( y' = f(y) . \)
Only few initial value problems, called also as Cauchy problems, can be solved analytically.
Let’s first solve a simple separable equation:
Problem: Consider the following initial value problem: y’=x-y, y(0)=1.
Solution: Try the following input in Maple.
> a:=diff(y(x),x)=x-y(x);
> dsolve(a,y(x));
> dsolve({a,y(0)=1},y(x));
As you can see, the general solution in Maple is expressed with a
constant represented by _C1. In the particular solution, the initial
conditions are applied and provides you an equation of y in terms of x.
Now let’s try a slightly more difficult problem:
Problem: Consider the following initial value problem: y’=(4-2/3x+4y)-1, y(0)=1.
Solution: Try the following input in Maple:
> b:= diff(y(x),x)=(4-2/3*x+4*y(x))^-1;
> dsolve(b,y(x));
> dsolve({b,y(0)=1},y(x));
Notice how for this example Maple gives and output with the
LambertW function because the initial differential equation we started
with is an inverse function, which when solved differentially yields the
LambertW function in Maple.
There are certain equations that Maple cannot solve analytically.
For example, we have an equation y’=x*x-sin(y). We enter it in Maple as
follows:
> dsolve(diff(y(x),x)=x^2-sin(y(x));
Interestingly enough, Maple calculates it, but does not give an output, even if calculated with an initial condition.
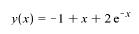
Example 1.2.3: Consider an autonomous differential equation \( y' = y^2 \cos (y) . \) We plot two solutions along with the direction field
(such plot is allso referred to as a phase portrait) using the following Maple script:
with(DEtools):
phaseportrait(diff(y(t), t) = (y(t)*y(t))*cos(y(t)), y, t = -5 .. 5, [y(0) = 1, y(0) = -1], y = -Pi .. Pi, color = aquamarine, linecolor = blue)

Deriving analytical solutions in Maple is a cumulative process.
This means that the more specific the answer is that you’re looking for,
the more steps you have to take to derive that answer. In general,
deriving analytical solutions is a two step process, which is solving
for a general solution and then solving for the particular solution.
I. Solving ODEs (General Solution)
Analytical solutions are one of the easiest topics to do in Maple
since Maple will do most of the work for you. All you need to know is
the differential equation and any initial conditions it may have to
obtain the general and particular solution.
In order to find the general solution, first define the ODE, and then use the dsolve command.
For example:
> ode:= diff(y(x),x)=2*y(x)+10;
> dsolve(ode)
As you can see, the _C1 seen in the output of the second command
line represents a constant, which would be normally written as “+C.”
The equation of y(x) is the general solution to the ODE.
Solving for a particular solution requires the same procedure as
solving for general solutions, except it requires including initial
conditions.First, define the initial conditions, then use the dsolve
command to solve the ODE subject to the initial conditions.
Let’s use the above ODE for this example:
> ics:=y(0)=1;
> dsolve({ode,ics});
Only a few initial value problems, called also as Cauchy problems, can be solved analytically.
Let’s first solve a simple separable equation:
Problem: Consider the following initial value problem: y’=x-y, y(0)=1.
Solution: Try the following input in Maple.
> a:=diff(y(x),x)=x-y(x);
> dsolve(a,y(x));
> dsolve({a,y(0)=1},y(x));
As you can see, the general solution in Maple is expressed with a
constant represented by _C1. In the particular solution, the initial
conditions are applied and provides you an equation of y in terms of x.
Now let’s try a slightly more difficult problem:
Problem: Consider the following initial value problem: y’=(4-2/3x+4y)-1, y(0)=1.
Solution: Try the following input in Maple:
> b:= diff(y(x),x)=(4-2/3*x+4*y(x))^-1;
> dsolve(b,y(x));
> dsolve({b,y(0)=1},y(x));
Notice how for this example Maple gives and output with the
LambertW function because the initial differential equation we started
with is an inverse function, which when solved differentially yields the
LambertW function in Maple.
There are certain equations that Maple cannot solve analytically.
For example, we have an equation y’=x*x-sin(y). We enter it in Maple as
follows:
> dsolve(diff(y(x),x)=x^2-sin(y(x));
Interestingly enough, Maple calculates it, but does not give an output, even if calculated with an initial condition.
Explanation of syntax:
Some parts of the syntax of the code may be confusing, so that will
be explained here.
You may wonder why the variable x[k] and y[k] are used instead of x(k)
and y(k). The reason is because the brackets [] resemble the denotation
you see. Therefore, x[k] and y[k] in actual form would be xk and yk
respectively. The parenthesis, on the other hand, would resemble the
independent variable relevant to the dependent variable in the
parenthesis.
The variable k1 denotes the equation f(x,y) which is subject to
differentiation in subsequent orders of the Taylor expansion. The
variables k2 is the differentiation of k1, and k3 is the differentiation
of k2, and so forth.
The lines with “for [variable] from [initial value] to [final
value] do” and “end do” is a loop. A loop in programming terms is
basically a recursion in which any computation that is entered between
these lines. The loop begins with the “for [variable] from [initial
value] to [final value] do” and ends with the “end do” or “od.” The
variable can be any value so long as the recursion uses that same
variable (If you use k, make sure to use k as the reference variable for
entering k-1, k+1, etc.). The initial value is the sequential number
that the recursion should begin with, which in this case should be 1.
The final value is the last sequential number that the recursion should
end with, which in this case should be 10, since 10 increments is enough
for a valid numerical approximation. The “end do” must be there for the
loop to end. If you do not put this, Maple will give you an error. To
avoid Maple from providing you with a long output, make sure to end all
lines with colons “:” instead of semi-colons “;”. This will suppress the
output into a smaller output.
I. Euler’s Method
*Refer to the Maple file “Euler’s Method”
*Euler method commands are available in
Maple, but this is to demonstrate how differential equations will be
calculated manually, which will also allow for plotting.
Using the
Euler command only requires one line of code, but this section will show
what calculations are conducted within that one line of code.
> with(Student[NumericalAnalysis]):
> Euler(diff(z(t),t)=1/(2*t-3*z(t)+5),z(0)=1,t=1,output=plot);
The Euler’s method takes the current y term and adds it with the
difference of the current and next x term multiplied by the function in
terms of the current x and y terms to yield the next y term.
Therefore, the generic Maple syntax will be as follows:
> f:= some equation
> x[0]:= some value
> y[0]:= some value
> h:= some value # represents the difference between the x terms, x[k+1]-x[k]
> for k from 0 to 9 do
> x[k+1]:=x[k]+h:
> y[k+1]:=y[k]+h*f(x[k],y[k]):
> end do
Let’s apply this syntax to an example where we have a differential
equation of y’=1/(2x-3y+5) and the initial conditions are y(0)=1 and
h=0.1 (This equation and initial conditions will be used in subsequent
examples):
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for k from 1 to 10 do
> x[k]:=k*h:
> y[k]:=y[k-1]+h*f(x[k-1],y[k-1]):
> end do
*Refer to the Maple file “Backward Euler’s Method”
The Backward Euler’s method is another method of approximation. The
syntax of the Backwards Euler Method is much like the Euler Method but
instead of multiplying the value step size (h) by the value of function
in the current term, it is multiplied by the value of the function of
the next term.
Therefore, the Maple syntax will be as follows:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:= 0:
> y[0]:= 1:
> h:= 0.1:
> for k from 0 to 9 do
> x[k+1]:= x[k]+h:
> bb := solve(b=y[k]+h*f(x[k+1],b),b);
> y[k+1]:= evalf(min(bb));
> end do;
The minimum is determined here because this is a quadratic equation which has 2 roots and thus we much choose the smaller root.
*Refer to the Maple file “Trapezoid Rule”
The concept of the Trapezoidal Rule in numerical methods is similar
to the trapezoidal rule of Riemann sums. The Trapezoid Rule is
generally more accurate than the above approximations, and it calculates
approximations by taking the sum of the function of the current and
next term and multiplying it by half the value of h.
Therefore the Maple syntax will be as follows:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:= 0:
> y[0]:= 1:
> h:= 0.1:
> for k from 0 to 9 do
> x[k+1]:= x[k]+h:
> bb := solve(b=y[k]+(h/2)*(f(x[k],y[n])+f(x[n+1],b)),b);
> y[k+1]:= evalf(min(bb));
> end do;
*Refer to the Maple file “Improved Euler’s Method”
The Improved Euler’s method, also known as the Heun formula or the
average slope method, gives a more accurate approximation than the
trapezoid rule and gives an explicit formula for computing y(n+1) in
terms of the values of x. The syntax of the Improved Euler’s method is
similar to that of the trapezoid rule, but the y value of the function
in terms of y(n+1) consists of the sum of the y value and the product of
h and the function in terms of x(n) and y(n).
Therefore, the Maple syntax will be as follows:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for n from 1 to 10 do
> x[n]:=x[n]*h:
> ystar:=y[n-1]+h*f(x[n-1],y[n-1]):
> y[n]:=y[n-1]+(h/2)*(f(x[n-1],y[n-1])+f(x[n],ystar):
> od;
*Refer to the Maple file “Modified Euler’s Method”
The Modified Ruler’s method is also called the midpoint
approximation. This method reevaluates the slope throughout the
approximation. Instead of taking approximations with slopes provided in
the function, this method attempts to calculate more accurate
approximations by calculating slopes halfway through the line segment.
The syntax of the Modified Euler’s method involves the sum of the
current y term and the product of h with the function in terms of the
sum of the current x and half of h (which defines the x value) and the
sum of the current y and the product of the h value and the function in
terms of the current x and y values (which defines the y value).
Therefore, the Maple syntax is as follows:
f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for k from 1 to 10 do
> x[k]:=k*h:
> y[k]:=y[k-1]+h*f(x[k-1]+(h/2),y[k-1]+(h/2)*f(x[k-1],y[k-1])):
> end do
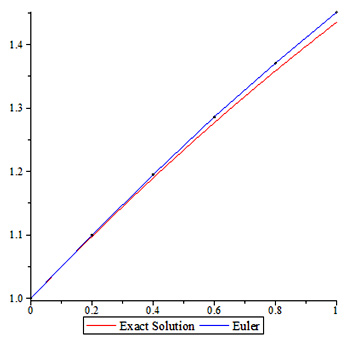
Let’s take all of the approximations and the exact values to compare the accuracy of the approximation methods: *Refer to the Maple file “Exact Values” for the exact values.
| x values |
Exact |
Euler |
Backwards Euler |
Trapezoid |
Improved Euler |
Modified Euler |
| 0.1 |
1.049370088 |
1.050000000 |
1.057930422 |
1.0493676 |
1.049390244 |
1.049382716 |
| 0.2 |
1.097463112 |
1.098780488 |
1.118582822 |
1.0974587 |
1.097594738 |
1.097488615 |
| 0.3 |
1.144258727 |
1.146316720 |
1.182399701 |
1.1442530 |
1.144322927 |
1.144297185 |
| 0.4 |
1.189743990 |
1.192590526 |
1.249960866 |
1.1897374 |
1.189831648 |
1.189795330 |
| 0.5 |
1.233913263 |
1.237590400 |
1.322052861 |
1.2339064 |
1.234025039 |
1.233977276 |
| 0.6 |
1.276767932 |
1.281311430 |
1.399792164 |
1.2767613 |
1.276904264 |
1.276844291 |
| 0.7 |
1.318315972 |
1.323755068 |
1.484864962 |
1.3183102 |
1.318477088 |
1.318404257 |
| 0.8 |
1.358571394 |
1.364928769 |
1.580059507 |
1.3585670 |
1.358757326 |
1.358671110 |
| 0.9 |
1.397553600 |
1.404845524 |
1.690720431 |
1.3975511 |
1.397764204 |
1.397664201 |
| 1.0 |
1.435286691 |
1.443523310 |
1.830688225 |
1.4352865 |
1.435521666 |
1.435407596 |
| Accuracy |
N/A |
99.4261% |
72.4513% |
99.9999% |
99.9836% |
99.9916% |
Notice how each improved approximation approaches the exact value,
which results in the modified Euler’s method being the most accurate
method of approximating the value of the differential equation
y’=1/(2*x-3*y+5). Note that the modified Euler’s method isn’t always the
most accurate approximation method, as the improved Euler’s method can
be more accurate than the modified Euler’s method depending on the
differential equation in question.
*The examples used for this section is related to the Cauchy example in the Analytical Solutions chapter.
VI. First Order Polynomial Approximation
*Refer to Maple file “First Order Polynomial Approximation”
Approximations using Taylor series expansions is a much easier task
to perform using Maple because there are many iterations of the same
calculations performed in order to achieve the desired answer.
Approximations with using Taylor series expansions in the first-order is actually the Euler algorithm: yn+1=yn+hf(xn,yn)=yn+h/(1-2xn+yn), n=0,1,2,…
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for k from 0 to 9 do
> x[k+1]:=x[k]+h:
> y[k+1]:=y[k]+h*f(x[k],y[k]):
> end do
They are similar in that they both take in the current term and add
the approximate deviation to the next term in order to yield the value
of the next term.
If you look at the Maple file, the approximation of the sequence is the
last y term of the sequence, which in this case is y10=1.443523310.
For each step in the sequence, the expansion requires 3 addition, 1
subtraction, 3 multiplication, and 1 division operations. Since there
are 8 steps to this sequence, in order to obtain the desired
approximation, the code performs 80 operations, which would be hectic
work to do by hand.
*Refer to Maple file “Second Order Polynomial Approximation”
The second order Taylor approximation is just adding the second
order differential deviation to the next term in the same equation used
for the first order Taylor expansion. The approximation is
y10=1.435290196. This algorithm requires 22 operations per step, which
means that the entire sequence requires 220 steps. However, this is not
significant since Maple does all the work.
Here is the syntax for the second order Taylor approximation:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for k from 0 to 9 do
> x[k+1]:=x[k]+h:
> k1:=f(x[k],y[k]):
> k2:=-(4*x[k]-6*y[k]+7)/2*x[k]-3*y[k]+5)^3:
> y[k+1]:=y[k]+h*k1+k2*h^2/2:
> end do:
> taylorapproximation2:=seq([x[k],y[k]],k=0..10);
*Notice that the taylorapproximation2
yields only the final values of x and y as opposed to showing all values
determined for each equation within the recursion.
The above syntax is correct if the y” of the original differential
equation (represented by k2) is solved by hand. However, there is a way
to work around this to lessen handwork and let Maple do a majority of
the work.
*Refer to Maple file “Second Order Polynomial Approximation Other Method”
Inside the loop, all you have to do is rewrite k2 and insert
additional code to let Maple solve the derivative of the differential
equation in terms of x and y.
Below would be the revised loop for the second order Taylor approximation:
> for k from 0 to 9 do
> x[k+1]:=x[k]+h:
> k1:=f(x[k],y[k]):
> fx:=subs(t=x[k],u=y[k],diff(f(t,u),t)) :
> fy:=subs(t=x[k],u=y[k],diff(f(t,u),u)) :
> k2:=(fx+fy*k1):
> y[k+1]:=y[k]+h*k1+k2*h^2/2:
> end do:
> taylorapproximation2:=seq([x[k],y[k]],k=0..10);
*Refer to Maple file “Third Order Polynomial Approximation”
The third order Taylor approximation is adding a third order
differential deviation to the equation for the 2nd order expansion. The
approximation for this is y10=1.435283295.
Here is the syntax for the third order Taylor approximation:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=1:
> y[0]:=2:
> h:=0.1:
> for k from 0 to 9 do
> x[k+1]:=x[k]+h:
> k1:=f(x[k],y[k]):
> fx:=subs(t=x[k],u=y[k],diff(f(t,u),t)) :
> fy:=subs(t=x[k],u=y[k],diff(f(t,u),u)) :
> k2:=(fx+fy*k1):
> fxx:=subs(t=x[k],u=[k],diff(f(t,u),t,t)):
> fxy:=subs(t=x[k],u=[k],diff(f(t,u),t,u)):
> fyy:=subs(t=x[k],u=[k],diff(f(t,u),u,u)):
> k3:= (fxx+2*fxy*k1+fyy*k1^2+fx*fy+fy^2*k1):
> y[k+1]:=y[k]+h*k1+k2*h^2/2+h^3/6*k3:
> end do:
> thirdtaylorapproximation:=seq([x[k],y[k]],k=0..10);
The total number of numerical operations here is 420. It is obvious
at this point why using mathematical programs such as Maple is a
desired approach for such problems.
*The example for this section is
related to the Cauchy example in the Analytical Solutions chapter and
Taylor Approximations section of this chapter.”
*Refer to the Maple file “Plotting and log plotting.”
Plotting the absolute value of the errors for Taylor
approximations, such as the ones from the previous example, is fairly
easy to do in normal plotting.
The normal plotting procedure involves taking all of the
information in the three Maple files regarding the Taylor approximations
and putting them into one file, then calculate the exact solution, then
find the difference between each approximation and the exact solution,
and plotting the solution.
Looking at the code, the syntax is pretty much self-explanatory.
The only part that may confuse students is the syntax for the plot
command. The plot command need not be in the same syntax as the file has
it. If you wish to, you can alter the syntax to form a curve instead of
dots.
Log-plotting is not much different than plotting normally. In other
programs such as Mathematica, there are a couple of fixes to make, but
in Maple only one line of code is required, as seen in the file. Make
sure that before you use the logplot command to open the plots package.
*Refer to the Maple file “Runge-Kutta Method.”
The most common order of Runge-Kutta method used is the fourth
order, in which four iterations of calculations are used to make an
approximation. The first and second orders do exist, but the Euler
methods actually are Runge-Kutta methods. The standard Euler’s method is
the first order Runge-Kutta method, and the Improved Euler’s Method is
the second order Runge-Kutta method.
The fourth order Runge-Kutta method is a slightly different method
of approximation, since it incorporates more levels of iterations to
narrow down approximations. For this method, we will use the same
non-linear differential equation we have used for the Euler methods and
Polynomial approximations.
The syntax for this method is as follows:
> f:= (x,y)->1/(2*x-3*y+5);
> x[0]:=0:
> y[0]:=1:
> h:=0.1:
> for n from 1 to 10 do
> x[n]:=n*h:
> k1:=f(x[n-1],y[n-1]):
> k2:=f(x[n-1]+(h/2),y[n-1]+(h/2)*k1):
> k3:=f(x[n-1]+(h/2),y[n-1]+(h/2)*k2):
> k4:=f(x[n-1]+h,y[n-1]+h*k3):
> y[n]:=y[n-1]+(1/6)*(k1+2*k2+2*k3+k4):
> od;
Now, let’s compare the exact value and the values determined by the polynomial approximations and the Runge-Kutta method.
| x values |
Exact |
First Order Polynomial |
Second Order Polynomial |
Third Order Polynomial |
Runge-Kutta Method |
| 0.1 |
1.049370088 |
1.050000000 |
1.049375000 |
1.049369792 |
1.049370096 |
| 0.2 |
1.097463112 |
1.098780488 |
1.097472078 |
1.097462488 |
1.097463129 |
| 0.3 |
1.144258727 |
1.146316720 |
1.144270767 |
1.144257750 |
1.144258752 |
| 0.4 |
1.189743990 |
1.192590526 |
1.189758039 |
1.189742647 |
1.189744023 |
| 0.5 |
1.233913263 |
1.237590400 |
1.233928208 |
1.233911548 |
1.233913304 |
| 0.6 |
1.276767932 |
1.281311430 |
1.276782652 |
1.276765849 |
1.276767980 |
| 0.7 |
1.318315972 |
1.323755068 |
1.318329371 |
1.318313532 |
1.318316028 |
| 0.8 |
1.358571394 |
1.364928769 |
1.358582430 |
1.358568614 |
1.358571457 |
| 0.9 |
1.397553600 |
1.404845524 |
1.397561307 |
1.397550500 |
1.397553670 |
| 1.0 |
1.435286691 |
1.443523310 |
1.435290196 |
1.435283295 |
1.435286767 |
| Accuracy |
N/A |
99.4261% |
99.99975% |
99.99976% |
99.99999% |
You will notice that compared to the Euler methods, these methods
of approximation are much more accurate because they contains much more
iterations of calculations than the Euler methods, which increases the
accuracy of the resulting y-value for each of the above methods.
Laplace transforms and Inverse Laplace Transforms
Laplace transforms in Maple is really straightforward and doesn’t require any complicated loops like the numerical methods.
For example, let’s take the equation t^2+sin(t)=y(t) as our
equation. The syntax for finding the laplace transform of this equation
requires the simple syntax below:
> with(inttrans):
> laplace (t^2+sin(t)=y(t),t,s) ;
Yes, that is all. Easy, right? The syntax for the command is (equation, dependent value, independent value).
Finding the inverse Laplace transform requires a similar syntax.
Just take the result we have from the Laplace transform above and apply
it here:
> with(inttrans):
> invlaplace ((2/s^3)+(1/s^2+1),s,t);
Very easy indeed. The syntax for the inverse Laplace transform is
reversed compared to the Laplace transform for some reason. The syntax
is (equation, independent value, dependent value).
Solving equations with periodic piecewise continuous functions
> with(plots):
> with(inttrans):
> E:=1; a:=2;
> yh :=t->invlaplace((x+5+2)/(x^2+5*x+6), x, t);
> p := x^2+5*x+6;
> yp1 := t->invlaplace(E/(a*x^2*(x^2+5x+6)),x,t)
> yp2 := t->invlaplace(E*exp(-a*x)/(x*p*(1-exp(-a*x))), x, t)
> y := t-> yp1(t)-piecewise(a < t, yp2(t-a), 2*a < t, yp2(t-2*a), 3*a < t, yp2(t-3*a))
> plot(y(t), t = 0 .. 4*a);
> y2 := t->y(t)+yh(t)
> plot(y2(t), t = 0 .. 4*a);