Linear Systems of Algebraic Equations

This page presents some topics from Linear Algebra needed for construction of solutions to systems of linear algebraic equations and some applications. We use matrices and vectors as essential elements in obtaining and expressing the solutions.

Reflection

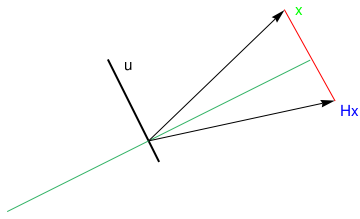
Suppose that we are given a line spanned over the vector a in \( \mathbb{R}^n , \) and we need to find a matrix H of reflection about the line through the origin in the plane. This matrix H should fix every vector on line, and should send any vector not on the line to its mirror image about the line. The subspace \( {\bf a}^{\perp} \) is called the hyperplane in \( \mathbb{R}^n , \) orthogonal to a. The \( n \times n \) orthogonal matrix

\[ {\bf H}_{\bf a} = {\bf I}_n - \frac{2}{{\bf a}^{\mathrm T} {\bf a}} \, {\bf a} \, {\bf a}^{\mathrm T} = {\bf I}_n - \frac{2}{\| {\bf a} \|^2} \, {\bf a} \, {\bf a}^{\mathrm T} \]

is called the Householder matrix or the Householder reflection about a, named in honor of the American mathematician Alston Householder (1904--1993). A. Householder is one of the pioneers of modern numerical linear algebra. He was a member of the mathematics division of Oak Ridge National Laboratory for over 20 years, from 1946 until 1969, and was also a Professor at the University of Tennessee. The complexity of the Householder algorithm is \( 2mn^2 - (2/3)\, n^3 \) flops (arithmetic operations). The Householder matrix \( {\bf H}_{\bf a} \) is symmetric, orthogonal, diagonalizable, and all its eigenvalues are 1's except one which is -1. Moreover, it is idempotent: \( {\bf H}_{\bf a}^2 = {\bf I} . \) When \( {\bf H}_{\bf a} \) is applied to a vector x, it reflects x through hyperplane \( \left\{ {\bf z} \, : \, {\bf a}^{\mathrm T} {\bf z} =0 \right\} . \)

Householder reflections are the preferred tool for computing the QR decomposition. Compare the unitary matrix \( {\bf H}_{\bf a} \) with projector

\[ {\bf P}_{\perp\bf a} = {\bf I}_n - \frac{1}{{\bf a}^{\mathrm T} {\bf a}} \, {\bf a} \, {\bf a}^{\mathrm T} \quad\mbox{or}\quad {\bf P}_{\perp\bf a} = {\bf I}_n - \frac{{\bf a} \, {\bf a}^{\ast}}{{\bf a}^{\ast} {\bf a}} . \]

Theorem: Reflection operator through a line that forms angle θ with positive abscissa on the plane is

\[ {\bf H}_{\theta} = \begin{bmatrix} \cos 2 \theta & \sin 2\theta \\ \sin 2\theta & -\cos 2 \theta \end{bmatrix} . \]

Example. We present some simple reflections on the plane and in 3D in the following tables.

Operator	Illustration	Standard Matrix
Reflection about the x-axis T(x,y) = (x,-y)		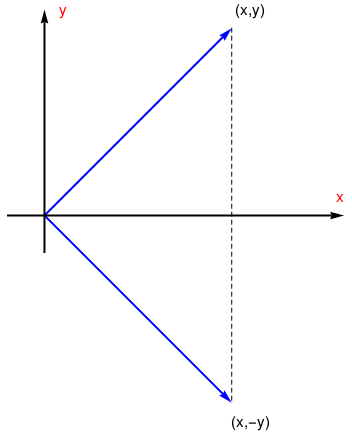\( \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix} \)
Reflection about the y-axis T(x,y)=(-x,y)		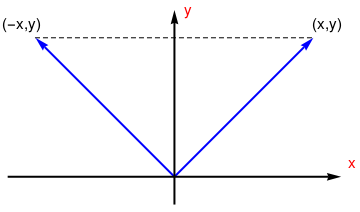\( \begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix} \)
Reflection about the line y=x T(x,y)=(y,x)		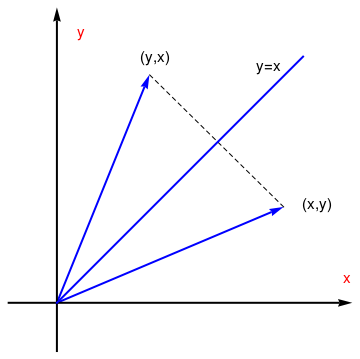\( \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} \)

Operator	Illustration	Standard Matrix
Reflection about the xy-plane T(x,y,z) = (x,y,-z)		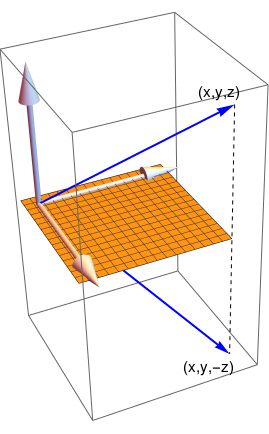\( \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{bmatrix} \)
Reflection about the xz-plane T(x,y,z)=(x,-y,z)		\( \begin{bmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{bmatrix} \)
Reflection about the yz-plane T(x,y,z)=(-x,y,z)		\( \begin{bmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \)

Example. Consider the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} . \) Then the Householder reflection with respect to vector u is

\[ {\bf H}_{\bf u} = {\bf I} - \frac{2}{9} \, {\bf u} \,{\bf u}^{\mathrm T} = \frac{1}{9} \begin{bmatrix} 7&4&-4 \\ 4&1&8 \\ -4&8&1 \end{bmatrix} . \]

The orthogonal symmetric matrix \( {\bf H}_{\bf u} \) is indeed a reflection because its eigenvalues are -1,1,1, and it is idempotent.

Example. Multiplication by the matrix

\[ {\bf A} = \begin{bmatrix} -1&0 \\ 0& -1 \end{bmatrix} \]

has the geometrical effect of reflecting the unit square about the origin. From the equation

\[ {\bf A} = \begin{bmatrix} -1&0 \\ 0& -1 \end{bmatrix} = \begin{bmatrix} -1&0 \\ 0& 1 \end{bmatrix} \, \begin{bmatrix} 1&0 \\ 0& -1 \end{bmatrix} , \]

it follows that multiplication by A is equivalent to reflection about x-axis and then reflection about the y-axis. On the other hand, multiplication by the matrix

\[ {\bf B} = \begin{bmatrix} 0&-1 \\ -1& 0 \end{bmatrix} \]

reflects about the line y = -x.

Theorem: If u and v are distinct vectors in \( \mathbb{R}^n \) with the same norm, then the Householder reflection about the hyperplane \( \left( {\bf u} - {\bf v} \right)^{\perp} \) maps u into v and conversely. ■

We check this theorem for two-dimensional column vectors \( {\bf u} = \left[ u_1 , u_2 \right]^{\mathrm T} \) and \( {\bf v} = \left[ v_1 , v_2 \right]^{\mathrm T} \) of the same norm. So given \( \| {\bf v} \| = \| {\bf u} \| , \) we calculate

\[ \| {\bf u} - {\bf v} \|^2 = \| {\bf u} \|^2 + \| {\bf v} \|^2 - \langle {\bf u}, {\bf v} \rangle - \langle {\bf v} , {\bf u} \rangle = 2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) . \]

Then we apply the Householder reflection \( {\bf H}_{{\bf u} - {\bf v}} \) to the vector u:

\begin{align*} {\bf H}_{{\bf u} - {\bf v}} {\bf u} &= {\bf u} - \frac{2}{\| {\bf u} - {\bf v} \|^2} \begin{bmatrix} \left( u_1 - v_1 \right)^2 u_1 + \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_2 \\ \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_1 + \left( u_2 - v_2 \right)^2 u_2 \end{bmatrix} \\ &= \frac{1}{u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2} \begin{bmatrix} v_1 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \\ v2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \end{bmatrix} = {\bf v} . \end{align*}

Similarly, \( {\bf H}_{{\bf u} - {\bf v}} {\bf v} = {\bf u} . \)

Example. We find a Householder reflection that maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \) into a vector v that has zeroes as its second and third components. Since this vecor has to be of the same norm, we get \( {\bf v} = \left[ 3, 0 , 0 \right]^{\mathrm T} . \) Since \( {\bf a} = {\bf u} - {\bf v} = \left[ -2, -2 , 2 \right]^{\mathrm T} , \) the Householder reflection \( {\bf H}_{{\bf a}} = \frac{1}{3} \begin{bmatrix} 1&-2&2 \\ -2&1&2 \\ 2&2&1 \end{bmatrix} \) maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \) into a vector v. Matrix \( {\bf H}_{{\bf a}} \) is idempotent (\( {\bf H}_{{\bf a}}^2 = {\bf I} \) ) because its eigenvalues are -1, 1, 1. ■

sage: nsp.is_finite()
False

We use the Householder reflection to obtain an alternative version of LU-decomposition. Consider the following m-by-n matrix:

\[ {\bf A} = \begin{bmatrix} a & {\bf v}^{\mathrm T} \\ {\bf u} & {\bf E} \end{bmatrix} , \]

where u and v are m-1 and n-1 column vectors, respectively. Let σ be the 2-norm of the first column of A. That is, let

\[ \sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} . \]

Assume that σ is nonzero. Then the vector u in the matrix A can be annihilated using a Householder reflection given by

\[ {\bf P} = {\bf I} - \beta {\bf h}\, {\bf h}^{\mathrm T} , \]

where

\[ {\bf h} = \begin{bmatrix} 1 \\ {\bf z} \end{bmatrix} , \quad \beta = 1 + \frac{a}{\sigma_a} , \quad {\bf z} = \frac{\bf u}{\beta \sigma_a} , \quad \sigma_a = \mbox{sign}(a) \sigma . \]

It is helpful in what follows to define the vectors q and p as

\[ {\bf q} = {\bf E}^{\mathrm T} {\bf z} \qquad\mbox{and} \qquad {\bf p} = \beta \left( {\bf v} + {\bf q} \right) . \]

Then

\[ {\bf P}\,{\bf A} = \begin{bmatrix} \alpha & {\bf w}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} , \]

where

\[ \alpha = - \sigma_a , \quad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} , \quad {\bf K} = {\bf E} - {\bf z}\,{\bf p}^{\mathrm T} . \]

The above formulas suggest the following version of Householder transformations that access the entries of the matrix in a row by row manner.

Algorithm (Row-oriented vertion of Householder transformations):

Step 1: Compute \( \sigma_a \) and β

\[ \sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} , \qquad \sigma_a = \mbox{sign}(a) \,\sigma , \qquad \beta = a + \frac{a}{\sigma_a} . \]

Step 2: Compute the factor row \( \left( \alpha , {\bf w}^{\mathrm T} \right) : \)

\[ \alpha = - \sigma_a , \qquad {\bf z} = \frac{\bf u}{\beta \sigma_a} . \]

Compute the appropriate linear combination of the rows of A (except for the first column) by computing

\[ {\bf q}^{\mathrm T} = {\bf z}^{\mathrm T} {\bf E}, \qquad {\bf p}^{\mathrm T} = \beta \left( {\bf v}^{\mathrm T} + {\bf q}^{\mathrm T} \right) , \qquad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} . \]

Step 3: Apply Gaussian elimination using the pivot row and column from step 2:

\[ \begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf z} & {\bf E} \end{bmatrix} \, \rightarrow \, \begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} , \]

where \( {\bf K} = {\bf E} - {\bf z} \,{\bf p} ^{\mathrm T} . \) ■

This formulation of Householder transformations can be regarded as a special kind of Gauss elimination, where the pivot row is computed from a linear combination of the rows of the matrix, rather than being taken directly from it. The numerical stability of the process can be seen from the fact that \( |z_i | \le 1 \) and \( |w_j | \le \beta \le 2 \) for every entry in z and w.

The Householder algorithm is the most widely used algorithm for QR factorization (for instance, qr in MATLAB) because it is less sensitive to rounding error than Gram--Schmidt algorithm.