head> Mechanical Applications - Brown University Applied Mathematics

Mechanical Applications in MuPAD

Brown University Applied Mathematics

Plotting solutions to differential equations can be useful in not only math classes, but in a number of disciplines. Differential equations are used to model scenarios in mechanics, electricity and magnetism, neuroscience, ecology, and much more. In this section, we present some application in Mechanics.

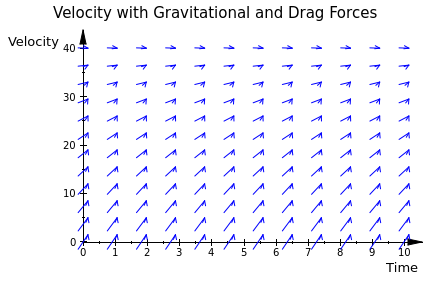
Example: When an object in free fall is being acted on by only the forces of air resistance (or some other fluid drag) and gravity, a differential equation can be written relating the acceleration to the velocity and two other constants describing these forces. For objects falling on earth, this equation is:

\[ \frac{{\text d}v}{{\text d}t} = \dot{v} = g - k\,v, \]
where k is a constant coefficient proportionallity. For simplicity, we assume that the drug force is proportional to the velocity. Such approximation is valid only for tiny objects falling from relatively small attitude. In reality, it is not true and the drug force depends on many circumstances, the main of which the the Reynolds number (the ratio of inertial forces to viscous forces). Here g is the acceleration due to gravity, which depends on latitude and the height under the ground. We can plot the direction (also called the slope) field for this differential equation to see how the velocity changes over time (we will take positive velocity to be pointing in the downward direction). In our example, we will assume k to be 0.25 1/s.

field := plot::VectorField2d([1, 10-0.25*y], x=0..10, y=0..40, Mesh=[12,12]):
plot(field, Header="Velocity with Gravitational and Drag Forces", AxesTitles=["Time","Velocity"]):

This is nice, because in 2 lines of code, you can get a perfectly good direction field to your exact specifications.

If we want to see how an object will approach terminal velocity (g=kv) based on its starting velocity, we can plot solution curves to the differential equation, as we have done in the past. The following plot shows the streamlines describing velocity as
  • xmax := 15: field := plot::VectorField2d([1, 10-0.25*y], x=0..xmax, y=0..40, Mesh=[12,12]):
    acceleration := (x,y) -> [10-0.25*y[1]]:
    solution1 := numeric::odesolve2(acceleration, 0, [0]):
    curve1 := plot::Function2d(solution1(x)[1], x=0..xmax, LineColor = RGB::Blue):
    solution2 := numeric::odesolve2(acceleration, 0, [20]):
    curve2 := plot::Function2d(solution2(x)[1], x=0..xmax, LineColor = RGB::Green):
    solution3 := numeric::odesolve2(acceleration, 0, [40]):
    curve3 := plot::Function2d(solution3(x)[1], x=0..xmax, LineColor = RGB::Red):
    plot(field, curve1, curve2, curve3, Header="Velocity with Gravitational and Drag Forces", AxesTitles=["Time","Velocity"]):

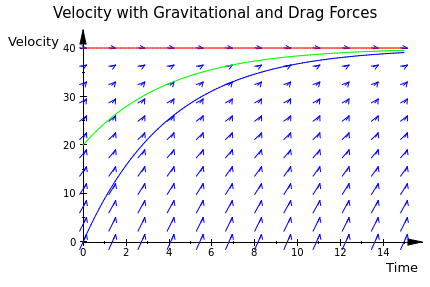
    Finally, you may want to clean the memory for further use:

    delete field, xmax, acceleration, solution1, curve1, solution2, curve2, solution3, curve3

    Example: Consider the mass--spring--pulley system shown in Figure, which we plot using the following script.

    string1 := plot::Line2d([3,6],[3,10]):
    string2 := plot::Line2d([7,6],[7,10]):
    radius := plot::Line2d([5,10],[7,10]):
    pulley := plot::Curve2d([2*sin(t)+5, 2*cos(t)+10]):
    mass1 := plot::Line2d([6.75,6],[7.25,6]):
    mass2 := plot::Line2d([6.5,5.25],[7.5,5.25]):
    mass3 := plot::Line2d([6.5,5.25],[6.75,6]):
    mass4 := plot::Line2d([7.25,6],[7.5,5.25]):
    spring1 := plot::Line2d([2.5,6],[3.5,6]):
    spring2 := plot::Line2d([3,6],[3.5,5.75]):
    spring3 := plot::Line2d([3.5,5.75],[2.5,5.25]):
    spring4 := plot::Line2d([2.5,5.25],[3.5,4.75]):
    spring5 := plot::Line2d([3.5,4.75],[2.5,4.25]):
    spring6 := plot::Line2d([2.5,4.25],[3,4]):
    spring7 := plot::Line2d([2.5,4],[3.5,4]):
    masslabel := plot::Text2d("m",[8,5.5]):
    springlabel := plot::Text2d("k",[1.75,5.25]):
    radiuslabel := plot::Text2d("R",[5.75,10.25]):
    eq := springlabel, string1, string2, radiuslabel, radius, masslabel, mass1, mass2, mass3, mass4, spring1, spring2, spring3, spring4, spring5, spring6, spring7, pulley:
    plot(eq, ViewingBox = [0..20,0..15], Axes = None):


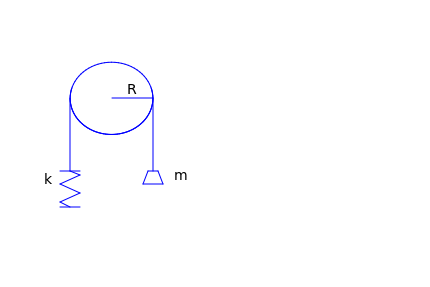
    It can be shown that the vibrations of this sytem can be modeled by the following differential equation:
    \[ \left( mR^2 + I \right) \frac{{\text d}^2 u}{{\text d}t^2} + k\,R^2 u =0, \]
    where \( u(t) \) is the displacement from equilibrium at time \( t \) of a weight of mass \( m ,\) the values \( R \) and \( I \) are the radius amd moment of inertia, respectively, of the pulley, and \( k \) is the spring constant according to Hooke's law.

    Home

    < Previous

    Next >