Complex numbers were introduced by the Italian famous gambler and mathematician Gerolamo Cardano (1501--1576) in 1545 while he found the explicit formula for all three roots of a cube equation. Many mathematicians contributed to the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli (baptized on 20 January 1526; died 1572). The notations 1 and i for unit vectors in horizontal positive direction and vertical positive direction, respectively, were introduced by Leonhard Euler (1707--1783) who visualized complex numbers as points with rectangular coordinates, but did not give a satisfactory foundation for complex numbers theory. He also suggested to drop the unit vector 1 in presenting vectors on the plane. It was Carl Friedrich Gauss (1777--1855) who introduced the term complex number. Cauchy, a French contemporary of Gauss, extended the concept of complex numbers to the notion of complex functions. University of Rhode Island professor Orlando Merino (born in 1954) has written an essay on history of discovery of complex numbers.
Complex numbers can be identified with three sets: points on the plane, denoted by ℝ², set of all (free) vectors on the plane, and the set of all ordered pairs of real numbers z = (x,y), where the first coordinate is denoted as ℜz = x and called for historical reasons real part of complex number z, and the second coordinate is denoted as ℑ ℜz = y and called the imaginary part of complex number z. A geometric plot of complex numbers as points z = x + jy using the x-axis as the real axis and y-axis as the imaginary axis is referred to as Argand diagram. Such plots are named after Jean-Robert Argand (1768–1822) who introduced it in 1806, although they were first described by Norwegian–Danish land surveyor and mathematician Caspar Wessel (1745–1818).
The set of complex numbers is one of the above three sets equipped with arithmetic operations (addition, subtraction, multiplication, and division) that satisfy usual axioms of real numbers. While addition and subtraction are inherited from vector algebra, multiplication and division satisfy specific rules based on the identity j² = -1.
For a long time it was thought that complex numbers were just toys invented and played with only by mathematicians. After all, no single quantity in the real world can be measured by an imaginary number, a number that lives only in the imagination of mathematicians. However, in 1926, Erwin Schrödinger (1887--1961) discovered that in the language of the world of the subatomic particles, complex numbers were the indispensable alphabet. Although no single measurable physical quantity corresponds to a complex number, a pair of physical quantities can be represented very naturally by a complex number. For instance, a wave, which always consists of an amplitude and a phase, begs a representation by a complex number.
?????? Sage has three different characters to represent the imaginary unit: I and two others are also used in Wolfram language when entered into worksheet with commands \[ImaginaryI] or \[ImaginaryJ], provide outputs 𝕚 or 𝕛, respectively.
Since there is no universal notation for a unit vector in vertical direction on the complex plane, Mathematica uses two of them: i and j. Euler suggested to use i (\( {\bf i}^2 =-1 \) ) , so mathematicians follow him; however, in engineering and computer science it is common to use j (\( {\bf j}^2 =-1 \) ) .
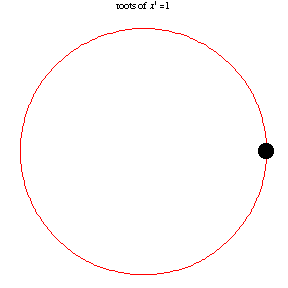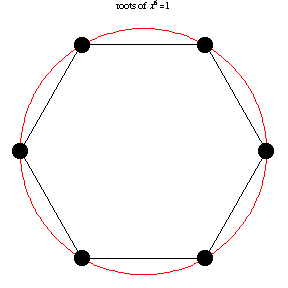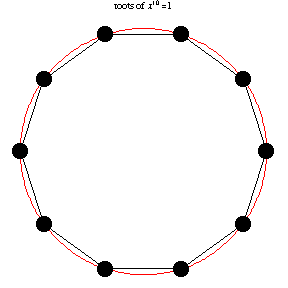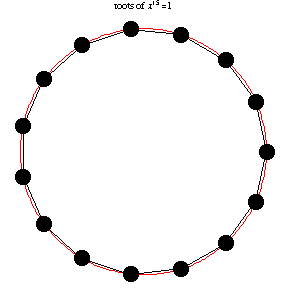
The following animation, developed by Wolfram Research, shows all n-th roots of unity
\( \left( 1 \right)^{1/n} = \sqrt[n]{1} \) for different positive integer values of
n: \( n=1,2,\ldots , 14 . \)