The Problem

In class, we discussed the solution of the following problem (called the Helmholtz Problem): Find u(x,y) such that

$$\nabla^2 u(x,y) - \lambda u(x,y) = f(x,y) \,\,\, on \,\,\, \Omega \\$$ (1)

$$u(x,y) = 0 \,\,\,on\,\,\, \partial\Omega.$$ (2)

where $\Omega = [-1,1] \times [-1,1]$ and $\lambda$ is some positive real constant. This problem is very similar to the Poisson Equation presented on pages 202-208, and the solution methodology will mimic that which is presented in the book.

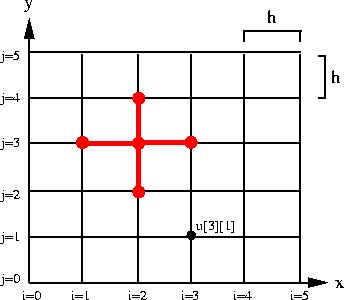
Assume we have created an equispaced grid (x_i,y_j) where $i,j = 0,\ldots,N-1$ and grid spacing h (see figure ). For notational simplicity, let u_ij and f_ij denote u(x_i,y_j)and f(x_i,y_j) respectively.

  

Figure: $5\times5$ equispaced grid with grid spacing h. A grid point u(x_i,y_j) is denoted in the C++ notation u[i][j]. For this problem we employ a five-point stencil (given in red).

In two dimensions, we can approximate $\nabla^2 u(x,y)$ using finite differencing by the following formula:

$$\frac{u_{i+1,j} + u_{i-1,j} - 4 u_{i,j} + u_{i,j+1} +u_{i+1,j-1}}{h^2}$$

We can evaluate $\lambda u(x,y)$ and f(x,y) as $\lambda u_{ij}$and f_ij respectively yielding the following approximation of the Helmholtz problem evaluated at the point (x_i,y_j):

$$\frac{u_{i+1,j} + u_{i-1,j} - 4 u_{ij} + u_{i,j+1} +u_{i+1,j-1}}{h^2} - \lambda u_{ij} = f_{ij}.$$

Following the book, we simplify by multiplying the expression by -h² yielding:

$$-u_{i+1,j} - u_{i-1,j} + (4+\mu) u_{ij} - u_{i,j+1} - u_{i+1,j-1} = q_{ij}$$

where $\mu = h^2 \lambda$ and q_ij = h² f_ij

Observe that we do not need to solve u(x,y) at the boundary because the value is given explicitly in the problem. Hence we only need to solve for those grid points interior to the domain. Because our goal is to form a system of the form ${\bf A} x = b$, we must now enumerate the interior grid points as in figure .

  

Figure: Left: Row-wise ordering of the interior points of the domain; Right: Column-wise ordering of the interior points of the domain.

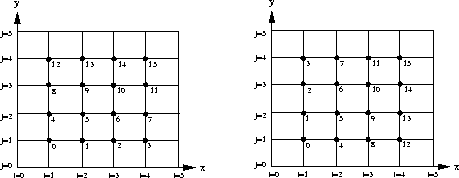Using a row-wise ordering and the fact that we know the solution at the boundaries, we form the matrix system ${\bf A}u=q$ given in figure .

  

Figure: Matrix system ${\bf A}u=q$

In class, we presented two means of solving this system: Jacobi Method and the (Preconditioned) Conjugate Gradient Method.