This page supports the main stream of the web site by providing/reminding some information regading Linear Algebra.
We demonstrate capabilities of MuPad for this topic.
Reflecttion
Reflection
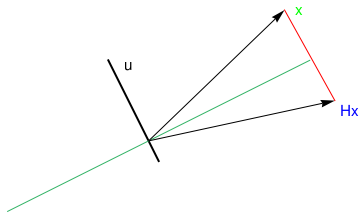
Suppose that we are given a line spanned over the vector
a in
\( \mathbb{R}^n , \) and we need to find a matrix
H
of reflection about the line through the origin in the plane. This matrix
H should fix every vector on line, and
should send any vector not on the line to its mirror image about the line. The subspace
\( {\bf a}^{\perp} \)
is called the hyperplane in
\( \mathbb{R}^n , \) orthogonal to
a. The
\( n \times n \)
orthogonal matrix
\[
{\bf H}_{\bf a} = {\bf I}_n - \frac{2}{{\bf a}^{\mathrm T} {\bf a}} \, {\bf a} \, {\bf a}^{\mathrm T}
= {\bf I}_n - \frac{2}{\| {\bf a} \|^2} \, {\bf a} \, {\bf a}^{\mathrm T}
\]
is called the Householder matrix or the Householder reflection about
a, named in honor of the American mathematician Alston Householder (1904--1993).
The complexity of the Householder algorithm is \( 2mn^2 - (2/3)\, n^3 \) flops
(arithmetic operations). The Householder matrix \( {\bf H}_{\bf a} \) is symmetric,
orthogonal, diagonalizable, and all its eigenvalues are 1's except one which is -1. Moreover, it is idempotent:
\( {\bf H}_{\bf a}^2 = {\bf I} . \) When \( {\bf H}_{\bf a} \) is applied to a vector x,
it reflects x through hyperplane \( \left\{ {\bf z} \, : \, {\bf a}^{\mathrm T} {\bf z} =0 \right\} . \)
Example.
We present some simple reflections on the plane and in 3D in the following tables.
| Operator |
Illustration |
Standard Matrix |
Reflection about
the x-axis
T(x,y) = (x,-y) |
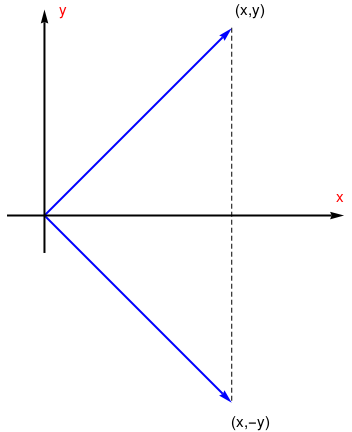 |
\( \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix} \) |
Reflection about
the y-axis
T(x,y)=(-x,y) |
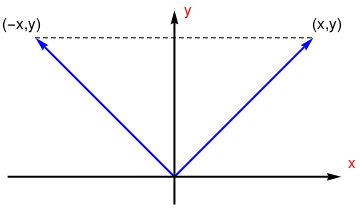 |
\( \begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix} \) |
Reflection about
the line y=x
T(x,y)=(y,x) |
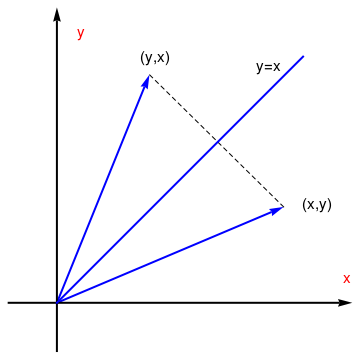 |
\( \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} \) |
| Operator |
Illustration |
Standard Matrix |
Reflection about
the xy-plane
T(x,y,z) = (x,y,-z) |
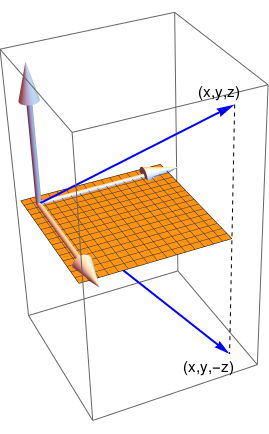 |
\( \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{bmatrix} \) |
Reflection about
the xz-plane
T(x,y,z)=(x,-y,z) |
 |
\( \begin{bmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{bmatrix} \) |
Reflection about
the yz-plane
T(x,y,z)=(-x,y,z) |
 |
\( \begin{bmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \) |
Example.
Consider the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} . \) Then the
Householder reflection with respect to vector u is
\[
{\bf H}_{\bf u} = {\bf I} - \frac{2}{9} \, {\bf u} \,{\bf u}^{\mathrm T} = \frac{1}{9} \begin{bmatrix} 7&4&-4 \\ 4&1&8 \\ -4&8&1 \end{bmatrix} .
\]
The orthogonal symmetric matrix
\( {\bf H}_{\bf u} \) is indeed a reflection because its eigenvalues are -1,1,1,
and it is idempotent.
Example. Multiplication by the matrix
\[
{\bf A} = \begin{bmatrix} -1&0 \\ 0& -1 \end{bmatrix}
\]
has the geometrical effect of reflecting the unit square about the origin. From the equation
\[
{\bf A} = \begin{bmatrix} -1&0 \\ 0& -1 \end{bmatrix} = \begin{bmatrix} -1&0 \\ 0& 1 \end{bmatrix} \, \begin{bmatrix} 1&0 \\ 0& -1 \end{bmatrix} ,
\]
it follows that multiplication by
A is equivalent to reflection about
x-axis and then reflection
about the
y-axis. On the other hand, multiplication by the matrix
\[
{\bf B} = \begin{bmatrix} 0&-1 \\ -1& 0 \end{bmatrix}
\]
reflects about the line
y = -x.
Theorem: If u and v are distinct vectors in
\( \mathbb{R}^n \) with the same norm, then the Householder reflection about the hyperplane
\( \left( {\bf u} - {\bf v} \right)^{\perp} \) maps u into v and conversely.
■
We check this theorem for two-dimensional vectors \( {\bf u} = \left[ u_1 , u_2 \right]^{\mathrm T} \)
and \( {\bf v} = \left[ v_1 , v_2 \right]^{\mathrm T} \) of the same norm. So given
\( \| {\bf v} \| = \| {\bf u} \| , \) we calculate
\[
\| {\bf u} - {\bf v} \|^2 = \| {\bf u} \|^2 + \| {\bf v} \|^2 - \langle {\bf u}, {\bf v} \rangle - \langle {\bf v} , {\bf u} \rangle =
2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) .
\]
Then we apply the Householder reflection
\( {\bf H}_{{\bf u} - {\bf v}} \) to the vector
u:
\begin{align*}
{\bf H}_{{\bf u} - {\bf v}} {\bf u} &= {\bf u} - \frac{2}{\| {\bf u} - {\bf v} \|^2}
\begin{bmatrix} \left( u_1 - v_1 \right)^2 u_1 + \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_2 \\
\left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_1 + \left( u_2 - v_2 \right)^2 u_2 \end{bmatrix} \\
&= \frac{1}{u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2} \begin{bmatrix} v_1 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \\
v2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \end{bmatrix} = {\bf v} .
\end{align*}
Similarly,
\( {\bf H}_{{\bf u} - {\bf v}} {\bf v} = {\bf u} . \) ■
Example.
We find a Householder reflection that maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \)
into a vector v that has zeroes as its second and third components. Since this vecor has to be of the same norm, we get
\( {\bf v} = \left[ 3, 0 , 0 \right]^{\mathrm T} . \) Since
\( {\bf a} = {\bf u} - {\bf v} = \left[ -2, -2 , 2 \right]^{\mathrm T} , \) the
Householder reflection \( {\bf H}_{{\bf a}} = \frac{1}{3} \begin{bmatrix} 1&-2&2 \\ -2&1&2 \\ 2&2&1 \end{bmatrix} \) maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \)
into a vector v. Matrix \( {\bf H}_{{\bf a}} \) is idempotent (\( {\bf H}_{{\bf a}}^2 = {\bf I} \) ) because its eigenvalues are -1, 1, 1. ■
sage: nsp.is_finite()
False
We use the Householder reflection to obtain an alternative version of LU-decomposition. Consider the following m-by-n matrix:
\[
{\bf A} = \begin{bmatrix} a & {\bf v}^{\mathrm T} \\ {\bf u} & {\bf E} \end{bmatrix} ,
\]
where
u and
v are
m-1 and
n-1 vectors, respectively. Let σ be the
2-norm of the first column of
A. That is, let
\[
\sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} .
\]
Assume that σ is nonzero. Then the vector
u in the matrix A can be annihilated using a
Householder reflection given by
\[
{\bf P} = {\bf I} - \beta {\bf h}\, {\bf h}^{\mathrm T} ,
\]
where
\[
{\bf h} = \begin{bmatrix} 1 \\ {\bf z} \end{bmatrix} , \quad \beta = 1 + \frac{a}{\sigma_a} , \quad {\bf z} = \frac{\bf u}{\beta \sigma_a} , \quad \sigma_a = \mbox{sign}(a) \sigma .
\]
It is helpful in what follows to define the vectors
q and
p as
\[
{\bf q} = {\bf E}^{\mathrm T} {\bf z} \qquad\mbox{and} \qquad {\bf p} = \beta \left( {\bf v} + {\bf q} \right) .
\]
Then
\[
{\bf P}\,{\bf A} = \begin{bmatrix} \alpha & {\bf w}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} ,
\]
where
\[
\alpha = - \sigma_a , \quad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} , \quad {\bf K} = {\bf E} - {\bf z}\,{\bf p}^{\mathrm T} .
\]
The above formulas suggest the following version of Householder transformations that access the entries of the matrix in a row by row manner.
Algorithm (Row-oriented vertion of Householder transformations):
Step 1: Compute \( \sigma_a \) and β
\[
\sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} , \qquad \sigma_a = \mbox{sign}(a) \,\sigma , \qquad \beta = a + \frac{a}{\sigma_a} .
\]
Step 2: Compute the factor row \( \left( \alpha , {\bf w}^{\mathrm T} \right) : \)
\[
\alpha = - \sigma_a , \qquad {\bf z} = \frac{\bf u}{\beta \sigma_a} .
\]
Compute the appropriate linear combination of the rows of
A (except for the first column) by computing
\[
{\bf q}^{\mathrm T} = {\bf z}^{\mathrm T} {\bf E}, \qquad {\bf p}^{\mathrm T} = \beta \left( {\bf v}^{\mathrm T} + {\bf q}^{\mathrm T} \right) , \qquad
{\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} .
\]
Step 3: Apply Gaussian elimination using the pivot row and column from step 2:
\[
\begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf z} & {\bf E} \end{bmatrix} \, \rightarrow \,
\begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} ,
\]
where
\( {\bf K} = {\bf E} - {\bf z} \,{\bf p} ^{\mathrm T} . \) ■
This formulation of Householder transformations can be regarded as a special kind of Gauss elimination, where the
pivot row is computed from a linear combination of the rows of the matrix, rather than being taken directly from it.
The numerical stability of the process can be seen from the fact that \( |z_i | \le 1 \) and
\( |w_j | \le \beta \le 2 \) for every entry in z and w.
The Householder algorithm is the most widely used algorithm for QR factorization (for instance, qr in MATLAB) because
it is less sensitive to rounding error than Gram--Schmidt algorithm.