 |
Sample ProblemsBrown University, Applied Mathematics |
Sample Differential Equations Problems
Example.Consider a pendulum equation
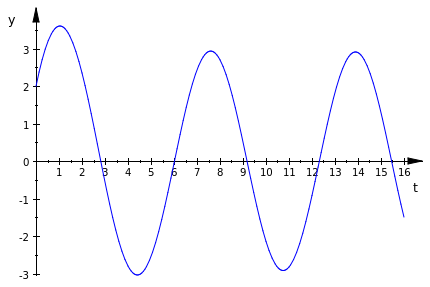
Example.Consider the nonhomogeneous equation for the second order linear differential equation:
\[ u''(t)+u'(t)+1.25*u(t)=3*\cos(t), \qquad u(0) = 2, \quad u'(0) = 3. \]
We solve and plot its solutions with the following steps:
p1 := ode::solve({q}, u(t))
{ sin(1.0 t) (0.1764705882 cos(2.0 t) + 0.7058823529 sin(2.0 t) + 3.0) + 1.294117647 e^(-0.5 t) cos(1.0 t) + 0.8235294117 e^(-0.5 t) sin(1.0 t) + cos(1.0 t) (0.7058823529 cos(2.0 t) - 0.1764705882 sin(2.0 t))}
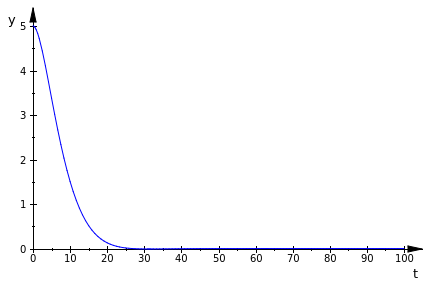
Example.Consider an RLC circuit. We solve the corresponding problem using the following MuPad code:
R := 2
C := 4
Kir := ode({L*Q''(t)+R*Q'(t)+(1/C)*Q(t)=0,Q(0)=5,Q'(0)=0},Q(t)) % define equation
sol := solve(Kir) % run solver
plotfunc2d((op(sol,1)),t=0..100)
Create your own problems to solve by picking one homogeneous equation and adding on a forcing term
Homogeneous Equations$y''(t)+9y(t) = 0 $
$8y''(t)-4y'(t) = 0 $
$y''(t)-5y'(t)+2y(t) = 0 $
$y''(t)-6y'(t)+9y(t) = 0 $
$y''(t)-4y(t) = 0 $
$12y''(t)-3y(t) = 0 $
$-14y''(t)+7y'(t) = 0 $
$17y''(t)-9y'(t)+16y(t) = 0 $
$y''(t)-y'(t)-3y(t) = 0 $
Forcing Terms
$t^2e^{3t}+6$
$17$
$3e^{4t}$
$19t^3+13t$
$-t^2$
$t^2cos(12t)$
$sin(-3x)$
$te^{4t}+6cos(-4t)$
$t+t^2+t^3+t^4$
$cos(19t)+tsin(-4t)+t^7e^{13t}$
Home |
< Previous |
Next > |