Consider the square 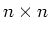$n \times n$ matrix with the following structure

$$A = \left [\begin{array}{cccccccc} 1 & \frac{1}{4 }& 0\ldo... ...ce*{.2in}\frac{1}{n+2} & \frac{1}{n} \end{array} \right ]$$

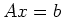Solve $Ax = b$ for $b^T = [1,2, \ldots n]^T$ using the following methods:

1. [I.] Thomas algorithm with computational cost ${\cal O}(n)$
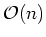
2. [II.] Steepest descent method

1. [(a)] Check how different your answers are in (I) and (II) for $n= 10,20,100$.
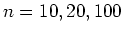2. [(b)] Estimate the wall-clock time to solve the system using (I) and (II).
3. [(c)] How does the number of iterations increase as 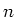$n$ increases in (II) and how does the total work scale.

Please write down your answers clearly and return your lists of codes.