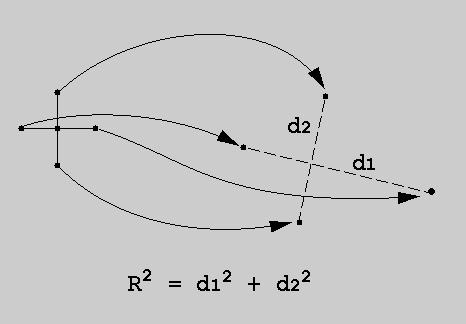
We begin with a regularly spaced grid of initial conditions.  The grid is advected both forward and backward in time for eight days.  A scalar value for each of the forward and backward time relative dispersion is assigned to each interior gridpoint by measuring the distance between the final positions of neighboring trajectories in the grid:

For initial conditions in the interior of a coherent structure (such as a vortex), relative dispersion is expected to be low.  On the other hand, boundaries of coherent structures are characterized by large values of relative dispersion.  In relation to the chaotic advection paradigm we wish to apply, local maxima of the forward time relative dispersion occur along material curves analogous to stable manifolds.  In contrast, local maxima in backward time occur along material curves analogous to unstable manifolds.  Similar ideas using a different Lagrangian diagnostic may be found at George Haller's web site  here .

As an example, consider the forced, damped Duffing oscillator.  The stable and unstable manifolds of the hyperbolic fixed point near the origin may be calculated using standard straddling methods, as we know a priori where to initialize the invariant manifold calculation (i.e. we know the approximate location of the hyperbolic fixed point):

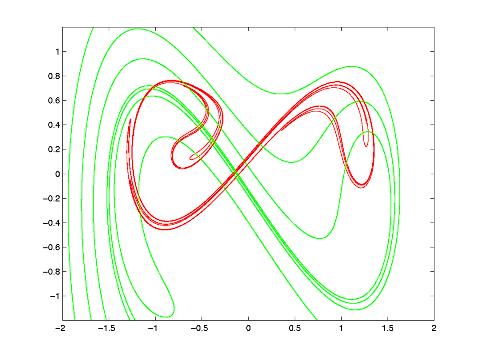
However, insight into this manifold geometry may be obtained via relative dispersion.  In image that follows, the green curve corresponds to local maxima of R in forward time, whereas the red curve corresponds to local maxima of R in backward time.

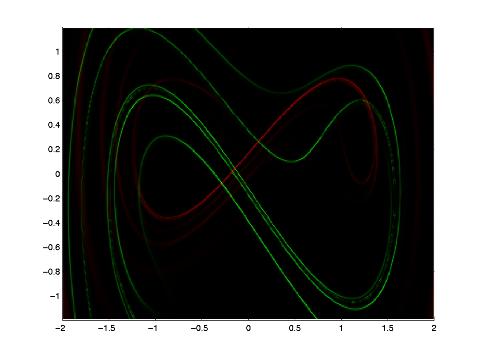
As expected, the relative dispersion approach is able to identify portions of the stable and unstable manifolds, with no a priori knowledge of the flow geometry.  This information is obtained by simply advecting a grid of tracers under the flow.  In particular, we see that we can identify the approximate location of the hyperbolic fixed point for the Duffing oscillator by the intersection of the forward and backward time maxima of R.