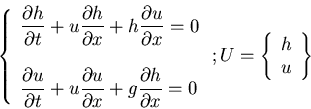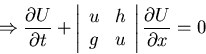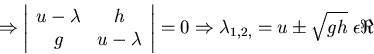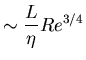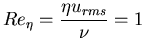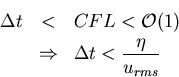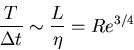CONTENTS
(Chapter :1 - Chapter: 9)
- Chapter 1:
- Introduction (2 lectures)
 Navier-Stokes: (u,p),
Navier-Stokes: (u,p),
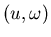 ,
Conservative Form, Approximations, B.C., Mathematical Nature, Computational
Complexity.
,
Conservative Form, Approximations, B.C., Mathematical Nature, Computational
Complexity.
- Chapter 2:
- The Finite Difference Method (4 lectures)
 Taylor Expansions, Difference Operators, Explicit Formulas, Fonberg's Construction, Implicit Formulas,
Lele's Approach, Example, Thomas's Algorithm for Periodic Matrices, Two-dimensional Stencils.
Taylor Expansions, Difference Operators, Explicit Formulas, Fonberg's Construction, Implicit Formulas,
Lele's Approach, Example, Thomas's Algorithm for Periodic Matrices, Two-dimensional Stencils.
- Chapter 3:
- Time-Stepping Algorithms (2 lectures)
 IVP, Consistency and Stability, Multi-step Methods (Derivation, Stability Regions), Polynomial Stability Methods.
IVP, Consistency and Stability, Multi-step Methods (Derivation, Stability Regions), Polynomial Stability Methods.
- Chapter 4:
- Parabolic Equation (2 lectures)
 Explicit/Implicit Schemes, Discrete Perturbation Analysis, von Neumann Analysis, Matrix Methods,
Spectra of Diffusion Operator, Iterative Methods of Elliptic Equations (Jacobi, Gauss Seidel,
Explicit/Implicit Schemes, Discrete Perturbation Analysis, von Neumann Analysis, Matrix Methods,
Spectra of Diffusion Operator, Iterative Methods of Elliptic Equations (Jacobi, Gauss Seidel, 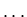 ).
).
- Chapter 5:
- Hyperbolic Equations
 Linear Advection Equations, Review of Basic Properties of PDEs, Euler-Forward/Center-Difference Scheme, Euler-Forward Upwind-Differencing Scheme, Lax-Friedrichs Scheme, Second-Order Upwind Scheme, Lax-Wendroff Scheme, Crank-Nicolson/Center Differencing Scheme, Adam-Bashford/Center-Differencing Scheme, Effects of Boundary Conditions, Finite Element Discretizations.
Linear Advection Equations, Review of Basic Properties of PDEs, Euler-Forward/Center-Difference Scheme, Euler-Forward Upwind-Differencing Scheme, Lax-Friedrichs Scheme, Second-Order Upwind Scheme, Lax-Wendroff Scheme, Crank-Nicolson/Center Differencing Scheme, Adam-Bashford/Center-Differencing Scheme, Effects of Boundary Conditions, Finite Element Discretizations.
- Chapter 6:
- Convection-Diffusion Equation
 The Peclet Number (Physical), Crank-Nicolson/Center Difference Scheme, Euler-Forward/Center Difference: Stability Condition, The (Numerical) Peclet Number Controversy; Mixed Explicit Schemes, Semi-Implicit Schemes, Boundary Conditions Normal Boundary Layers.
The Peclet Number (Physical), Crank-Nicolson/Center Difference Scheme, Euler-Forward/Center Difference: Stability Condition, The (Numerical) Peclet Number Controversy; Mixed Explicit Schemes, Semi-Implicit Schemes, Boundary Conditions Normal Boundary Layers.
- Chapter 7:
- Vorticity-Based Formulations
Vorticity Streamfunction Formulation
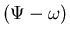 :
Governing Equations, Boundary Condition (Thom's Pearson's, Woods's) 1D Model
:
Governing Equations, Boundary Condition (Thom's Pearson's, Woods's) 1D Model
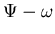 Formulation: Explicit Euler, Semi-Implicit, Full-Implicit; Green's Functions; Vorticity, Velocity Formulations: Green's Functions for 1D Model Problem, Penalty Method; Application in 2D: Flow Over a Backward Facing Step, Streamfunction-Only Formulation.
Formulation: Explicit Euler, Semi-Implicit, Full-Implicit; Green's Functions; Vorticity, Velocity Formulations: Green's Functions for 1D Model Problem, Penalty Method; Application in 2D: Flow Over a Backward Facing Step, Streamfunction-Only Formulation.
- Chapter 8:
- Navier-Stokes in Primitive Variables
Governing Equations-Pressure Interpretation, Stokes Model Problem, Staggered Mesh/Implicit Discretization: Discrete Poisson Equation, Green's Functions Implementation, MAC Grid; Non-Staggered Mesh (Implicit Discretization): Consistent 2D Poisson Equation, Discretization of Stoke Model Problem, Pressure Boundary Conditions, Classical Splitting Scheme, High-Order Splitting Scheme, Other Splitting Schemes; Staggered Mesh (Explicit Discretization), The Artificial Compressibility Methods: Basic Idea, MAC Discretization, The Choice of Parameter C, The Turkel Preconditioner, Stability of Artificial Compressibility Method, The Original Chorin Scheme.
- Chapter 9:
- Examples/Applications
Chapter 1: Introduction
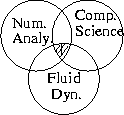
- CFD is often confused with Numerical Analysis and sometimes with Computer Science or
Fluid Dynamics but it is perhaps the intersection of all three:
- There is no official birth date of CFD but the 1965 article of
Harlow and Fromm in Scientific American (vol. 212, No. 3, pp 104-140) set the stage for computer experiments in
Fluid Dynamics and drew the analogy with the modern ``thought experiments'' of Fermi and Einstein.
- You are supposed to know, for example, the eigenvalues of
and properties of linear systems but you should also be able to distinguish between convective and diffusive
time scales in order to develop appropriate non-dimensionalizations.
- Also, simultaneous advances in computer hardware often suggest approriate algorithms. Case in point
is the Jacobi algorithm, obviously obsolete on serial computers in favor of the Gauss-Seidel algorithm in the seventies.
However, it was re-discovered in the eighties since straight Gauss-Seidel (G-S) is not easily parallelizable
(although the black-red G-S is!)
- In this course we will learn how to numerically formulate and solve the
incompressible Navier-Stokes equations in two- and three-dimensions,
covering fundamentals of different discretizations algorithms as well as formulations.
Incompressible Navier-Stokes Equations
-
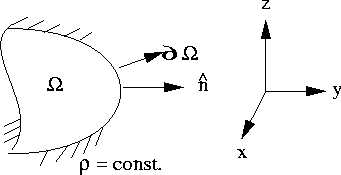
- I. Velocity-Pressure Formulation (primitive variables):
Eulerian description
where
is the stress tensor for incompressible fluids.
- *
- Pressure is not a thermodynamic quantity, i.e.
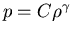 is not valid. It is a constraint,
projecting the solution
is not valid. It is a constraint,
projecting the solution
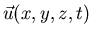 onto a divergence-free space. Otherwise it would overdetermine the system.
Note that
onto a divergence-free space. Otherwise it would overdetermine the system.
Note that
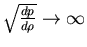 (sound speed). Therefore, disturbances propagate infinitely fast
in incompressible media.
(sound speed). Therefore, disturbances propagate infinitely fast
in incompressible media.
- *
- Viscous terms (assuming linear Newtonian shear stress law): It may be that
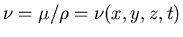 ,
then the full stress tensor should be used instead of
,
then the full stress tensor should be used instead of
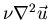 ,
i.e.
,
i.e.
![$\nabla \cdot [\nu(\nabla \vec{u} + \nabla^{T} \vec{u})]$](img17.gif) .
For example, in LES formulations,
.
For example, in LES formulations,
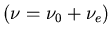 ,
or temperature-dependent viscosity in stability studies.
,
or temperature-dependent viscosity in stability studies.
- *
- Convective/Advective Terms:
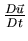 :
=
:
=
- Non-conservative:
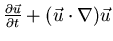 ,
convective-form
,
convective-form
- Consevative (Lax '54):
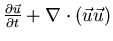 ,
flux-form, (basis of
finite volume schemes)
,
flux-form, (basis of
finite volume schemes)
- Rotational form:
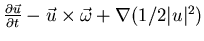
- Skew-symmetric:
![$ \frac{\partial \vec{u}}{\partial t} + \frac{1}{2} [ (\vec{u}\cdot \nabla )\vec{u}
+ \nabla \cdot (\vec{u}\vec{u})]$](img23.gif) ,
used for transport of species, e.g. temperature.
,
used for transport of species, e.g. temperature.
Note that the continuum forms are all equivalent but semi-discrete forms may differ.
* Semi-discrete forms for Non-Linear Terms in incompressible Navier-Stokes:
Ref: ``On the rotation and skew-symmetric forms for incompressible flow simulation,'' T.A. Zang, Appl. Num. Math.
For 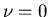 (inviscid, frictionless) flows and no source term
(inviscid, frictionless) flows and no source term
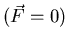 ,
the N-S conserve linear momentum
,
the N-S conserve linear momentum
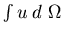 and kinetic energy
and kinetic energy
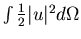 .
However, for semi-discrete system (i.e. continuous in time but discrete in space) we have:
.
However, for semi-discrete system (i.e. continuous in time but discrete in space) we have:
- Integral Forms (Galerkin) conserve both.
- Pointwise forms (collocation):
-
- rotational/skew-symmetric: conserve both
-
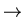
- divergence (flux): conserves only linear momentum
-
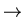
- convection (non-cons): unstable, conserves neither
-
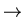
- alternate (divergence & convective): stable
*Computational Complexity:
- -
- Rotation: 6 derivatives
- -
- Skew- symm: 18 derivatives
- -
- Convective/divergence/alternate: 9 derivatives
*Conservation Property of Skew-Symmetric Form:
But
Note: Skew symmetric matirx
Note: If n = odd
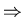
Review: The general Navier-Stokes equations are:
Newtonian:
Stokes hypothesis:
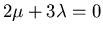 ,
from experimental evidence (equilibrium). Thus,
,
from experimental evidence (equilibrium). Thus,
constant 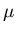 :
:
* Viscoelastic fluids:
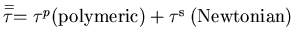 ;
;
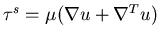
In Non-Newtonian fluids (e.g. blood flow), we then need
constitutive equations for 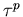 ,
the polymeric contributions, which are typically of hyperbolic nature, e.g.,
,
the polymeric contributions, which are typically of hyperbolic nature, e.g.,
where 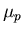 is the polymeric shear viscosity.
is the polymeric shear viscosity.
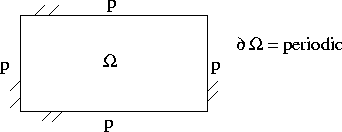
II. Velocity-Vorticity Formulation:
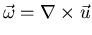
or
System (*) is equivalent to the
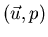 formulation. The proof, for simply-connected domains, is
done in 3 steps.
formulation. The proof, for simply-connected domains, is
done in 3 steps.
- 1.
-
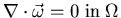 ?
?
- 2.
-
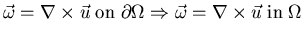
- 3.
-
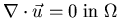 ?
?
on
III. Non-Dimensionalization:
We define
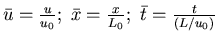
 Convective time scale
Convective time scale
then
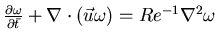 in 2D, which is appropriate for modest to large Re, where
in 2D, which is appropriate for modest to large Re, where
For
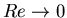 ,
we introduce the diffusive time scale
,
we introduce the diffusive time scale
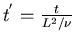 ,
therefore the 2D-vorticity equation is:
,
therefore the 2D-vorticity equation is:
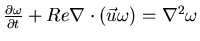 ,
which is more appropriate for low Re (creeping) flows.
,
which is more appropriate for low Re (creeping) flows.
*Velocity-pressure:
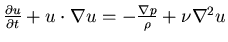 (dimensional)
(dimensional)
*
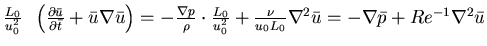 ,
where
,
where
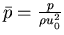
In summary: convective time units (fast):
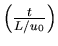 ,
and difffusive time scale (slow):
,
and difffusive time scale (slow):
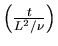
IV. Boundary Conditions:
 No-slip (Dirichlet)
Us = Uw implies perfect momentum exhange of molecules with wall, molecules stick on the wall. Valid for continuum media. (
No-slip (Dirichlet)
Us = Uw implies perfect momentum exhange of molecules with wall, molecules stick on the wall. Valid for continuum media. (
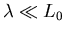 ;
the mean free path (in gases) much less than characteristic length scale)
;
the mean free path (in gases) much less than characteristic length scale)
Define
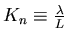 ,
Knudsen number
,
Knudsen number
If
Kn < 10-3, continuum
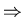 Direct Methods, (e.g., finite differences, finite elements, spectal methods). However, use Monte Carlo, Boltzmann for
Kn > 10-3; rarefied allows slip and thus, model b.c. as
Direct Methods, (e.g., finite differences, finite elements, spectal methods). However, use Monte Carlo, Boltzmann for
Kn > 10-3; rarefied allows slip and thus, model b.c. as
Applications: high-altitude, high-speed flows 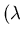 Large),
micro-mechanis (L small)
Large),
micro-mechanis (L small)
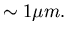 (
(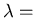 65 nm at STP).
65 nm at STP).
 No-penetration (Dirichlet)
For viscous or inviscid flows, in the norml direction we always have
No-penetration (Dirichlet)
For viscous or inviscid flows, in the norml direction we always have
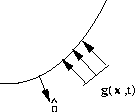
 Flux (Neumann b.c.)
Flux (Neumann b.c.)
 Robin b.c. - (heat transfer; mass transfer)
Robin b.c. - (heat transfer; mass transfer)
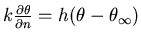 ,
where h = heat transfer coefficient.
,
where h = heat transfer coefficient.
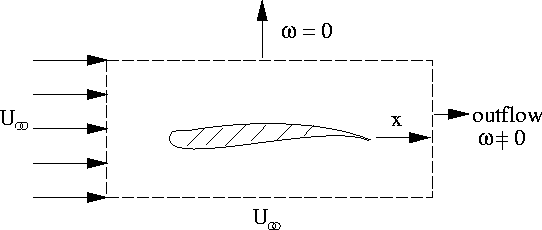
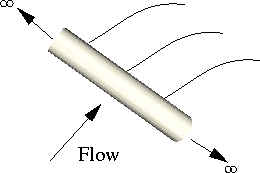
 Outflow boundary conditions: Flow past an airfoil:
Outflow boundary conditions: Flow past an airfoil:
outflow:
- mathematically required, not physically
- unknown state
- extrapolate, e.g.
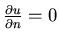 (with
(with
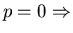 zero normal stress)
zero normal stress)
-
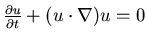 in a sponge or a buffer layer.
in a sponge or a buffer layer.
- parabolize the N.S. making singular the Laplacian operator, e.g.
![$\nabla \cdot [\nu(x)(\nabla u+\nabla^{\tau}u)] $](img88.gif)
NOTE: More difficult for incompressible than compressible where use of characteristics may work (not rigorous...)
Special Cases
2D Flow (does it exist?)
 2D geometry does not guarantee 2D flow. 3D for
Re > Rec, bifurcation. Instabilities (bifurcations) may develop. Vorticity
2D geometry does not guarantee 2D flow. 3D for
Re > Rec, bifurcation. Instabilities (bifurcations) may develop. Vorticity
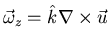 ,
perpendicular to 2D plane in 2D flow. Stretching term
,
perpendicular to 2D plane in 2D flow. Stretching term
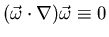 in 2D thus,
in 2D thus,
Define 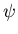 :
(stream function)
4th order for
:
(stream function)
4th order for 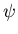 (3rd for BL):
(3rd for BL):
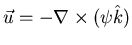 ,
and thus
,
and thus
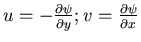 Continuity:
Continuity:
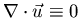 is satisfied automatically and
is satisfied automatically and
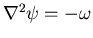 ,
expresses a kinematic constraint (it is not a time evolution equation).
,
expresses a kinematic constraint (it is not a time evolution equation).
For
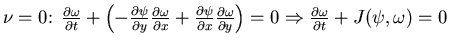
 steady state
steady state
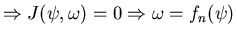 that is, in inviscid 2D steady flow, vorticity is constant along steamlines. Streamlines
that is, in inviscid 2D steady flow, vorticity is constant along steamlines. Streamlines 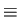 isovorticity lines
isovorticity lines
* Boundary Conditions: Too many for 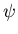 /Thom's b.c. None for
/Thom's b.c. None for 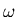 - create b.c. through local expansions and use the excessive
- create b.c. through local expansions and use the excessive 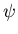 b.c.
b.c.
 Advantage: Incompressibility, the main headache in incompressible formulations, is honored automatically within discretization error. (Very popular method in the seventies.)
Advantage: Incompressibility, the main headache in incompressible formulations, is honored automatically within discretization error. (Very popular method in the seventies.)
Stokes (creeping) flow:
i.e. very viscous flows
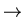 linear equations.
linear equations.
Applications: dispersion, combustion, particle flows small size
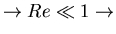 approximate as Stokes flow.
approximate as Stokes flow.
parabolic/elliptic problems.
- *
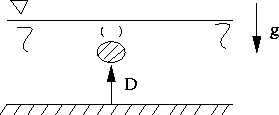
- Stokes drag of a sphere :
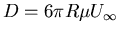
This is the oldest known analytical solution for a creeping flow (Stokes, 1851)
- *
- Here, we obtain symmetric solutions if geometry is symmetric. Contrast with symmetry-breaking bifurcations for finite Re.
Other complex shapes (particles): Boundary element methods
Inviscid flow:
e.g. high-speed flows

- hyperbolic equations

- There is some debate in the current literataure as to whether there exist singular solutions in incompressible flows, i.e.,
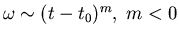 for t0 = finite.
for t0 = finite.

- Standard vortex methods (Chorin/Leonard) work well for simulations of inviscid flows.
V. Potential Flow:
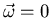 ,
,
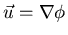 /incompressible, inviscid, irrotational flow, purely elliptic
/incompressible, inviscid, irrotational flow, purely elliptic
does it exist?
at sufficiently large distances
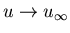 in freestream and
in freestream and
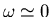 with
with 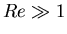
 Compressible:
Compressible:
+ energy equation
unknowns,
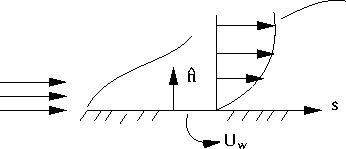
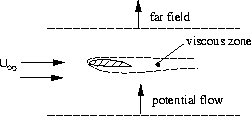
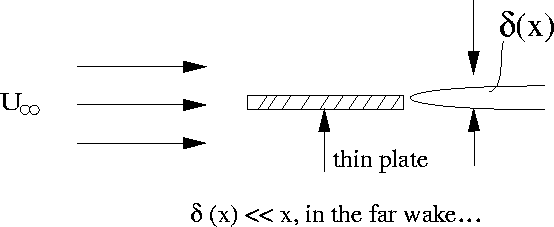
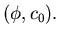 Boundary Layer Flow
Boundary Layer Flow
neglect streamwise diffusion compared to normal (cross) diffusion
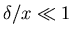 ,
e.g.
,
e.g.
great simplification, computation complexity in y-only; smaller domain.
*sometimes called the thin shear layer approximation
In steady state we also call them: Parapolized N-S if the predominant main flow direction equation is parabolic in
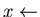 plays the role of time
plays the role of time
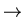 advance explicitly.
VI. Mathematical Nature of the Flow Equations
advance explicitly.
VI. Mathematical Nature of the Flow Equations
The balance of various terms in Navier-Stokes describes dominant diffusion or convection fluxes and thus the mathematical character of N-S will be varying from parabolic to hyperbolic depending on the flow problem.
 unsteady N-S: parabolic-hyperbolic; steady: elliptic-hyperbolic. The divergence-free constraint imposes the hyperbolicity.
unsteady N-S: parabolic-hyperbolic; steady: elliptic-hyperbolic. The divergence-free constraint imposes the hyperbolicity.
*Examples: Stokes equation/creeping flow
 steady state
steady state
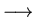 purely elliptic (for fixed
purely elliptic (for fixed
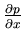 ).
).
 unsteady
unsteady
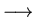 parabolic.
parabolic.
Outside the B.L. for 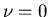 (high-speed flows) the governing equations are:
(high-speed flows) the governing equations are:
essentially a hyperbolic equation in space and time describing a propagation phenomenon. Inside the B.L. the governing equations are parabolic/hyperbolic.
PDEs of 2
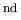 -order
-order (Review)
Where
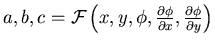 (not 2nd derivatives).
For example,
(not 2nd derivatives).
For example,
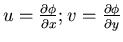 ,
where
,
where 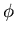 is the potential.
is the potential.
 Solution: wave of the form
Solution: wave of the form
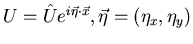 ,
,
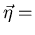 propagation vector. Therefore, by substitution
propagation vector. Therefore, by substitution
Example: Transonic-Inviscid Flow/Steady
Local Mach
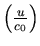 variation; c0 = speed of sound
variation; c0 = speed of sound
Determinant:
This mixed nature of the transonic potential equation has been a great challenge in CFD since the transition line between the subsonic and the supersonic regions is part of the solution. Note that for
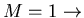 parabolic.
parabolic.
 Non-linear wave propagation (general model)
Non-linear wave propagation (general model)
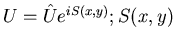 is the wave characteristic surface, if real
is the wave characteristic surface, if real
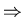 hyperbolic system. We thus consider,
hyperbolic system. We thus consider,
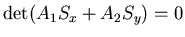 .
If we interpret
.
If we interpret
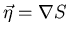 ,
normal to surface = direction of propagation, then
,
normal to surface = direction of propagation, then
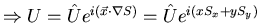
Then the tangent vectors of the surface are defined as:
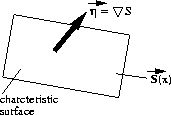
Thus, the direction of the chacteristic surface is given by:
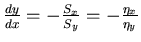
Note: The surface S(x,y) = const is a wavefront surface that separates the points already influenced by the propagating disturbance from the points not yet reached by the wave.
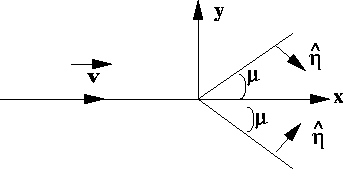
Example: Potential flow for a thin airfoil:
Directon of Characteristic
*System of
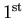 -order equations/Generalization
e.g. inviscid flows
conservation (flux) form:
-order equations/Generalization
e.g. inviscid flows
conservation (flux) form:
- n-equations
- m-dimensions (including time)
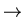 Quasi-linear form via Jacobian:
Quasi-linear form via Jacobian:
matrix form:
(summation)
Ak, Q = F(xk,U) do not depend on derivatives of U!!
A plane wave solution will exist with propagating direction
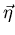 if
if
![$[A^{k}\eta_{k}]\hat{U} = 0 \Rightarrow \det (A^{k}\eta_{k})=0$](img164.gif) ,
where
,
where
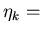 components of
components of
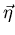 .
The solutions
.
The solutions
![$\vec{\eta} = [\eta_{k}], k=1,=\ldots, m$](img166.gif) are (n) altogether (equal to # of 1st order eqn)
are (n) altogether (equal to # of 1st order eqn)
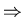 define characteristic surfaces from
define characteristic surfaces from
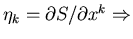 at most (n) characteristic surfaces.
at most (n) characteristic surfaces.
Definition:
- hyperbolic: for all n characteristic surfaces are real and linearly independent
- elliptic: all complex
- hybrid: some elliptic, some hyperbolic
- parabolic: if matrix
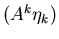 is not of rank (n), e.g. u1 has derivatives w.r.t. x1 missing
is not of rank (n), e.g. u1 has derivatives w.r.t. x1 missing
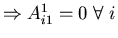 .
.
Example: 2 equations:
- if
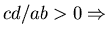 hyperbolic (e.g.
a = b=1, c=d=1),
hyperbolic (e.g.
a = b=1, c=d=1),
- if
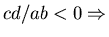 elliptic
elliptic
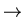 (e.g a=b=1 c=-d=-1)
(e.g a=b=1 c=-d=-1)
- if
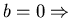 parabolic,
a=1, b=0, c=-d=-1, F1 =0, F2 = v
parabolic,
a=1, b=0, c=-d=-1, F1 =0, F2 = v
Exercise: Show that the Cauchy-Riemann equations are of elliptic type
Example: 2D Stationary shallow-water equations
where
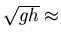 ``sonic'' speed,
``sonic'' speed,
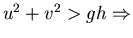 hyperbolic
hyperbolic
 Characteristic surface
Characteristic surface
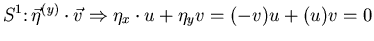
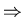 characteristic surface
characteristic surface 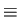 streamline surface.
streamline surface.
Example: Inviscid, Incompressible Equations (Euler)/steady
Define
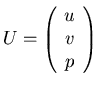 then
then
Thus,
Threfore, this system is hybrid since it has mixed eigenvalues.
*Time-dependent flows
We single out time from the system, e.g. xm = t,
equivalent to eigenvalue problem
where
(compare with
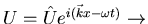 where,
where, 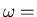 frequency either real or complex, and
frequency either real or complex, and
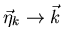
Example: 1D Time-dependent shallow water equations
Question: What is the 2D time-dependent shallow water?
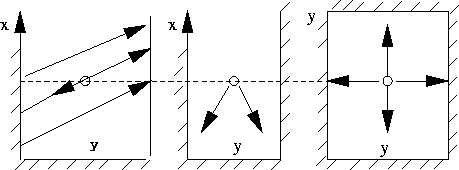
Domain of Dependence/Influence
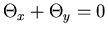 |
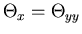 |
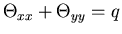 |
 hyperbolic
hyperbolic |
 parabolic
parabolic |
 elliptic
elliptic |
 IVP
IVP |
 IVP/BVD
IVP/BVD |
 BVP
BVP |
Computational Complexity of Navier-Stokes
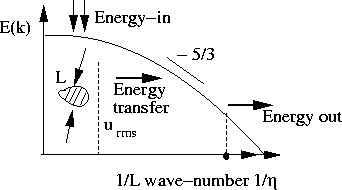
*At high Re Kolmogorov's scaling theory; also Foias's argument
Assume that L = size of a large eddy and that (urms) represents 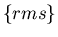 value. Also
value. Also 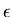 is the dissipation
is the dissipation
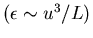 and
and 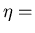 Kolmogorov's scale, which is the smallest scale of turbulence.
Kolmogorov's scale, which is the smallest scale of turbulence.
1D: disparity of scales
Number of Degrees of freedom
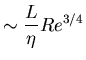
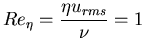
3D: scales carry energy
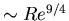
 Time scales: fast:
Time scales: fast:
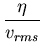 ;
slow:
;
slow:
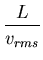
 Explicit integration in time dictates that we honor the CFL condition, i.e.,
Explicit integration in time dictates that we honor the CFL condition, i.e.,
 Need to integrate for long time
Need to integrate for long time
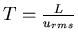 (one large eddy-turnover time). Thus, number of time steps:
(one large eddy-turnover time). Thus, number of time steps:
Thus total work
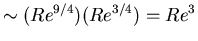 ,
so increasing Re by a factor of 2 leads to an order of magnitude increase in the CPU requirement.
,
so increasing Re by a factor of 2 leads to an order of magnitude increase in the CPU requirement.
Recommended Reading:
- (1)
- ``Computer Experiments in Fluid Dynamics,'' Harlow, F.H. and Fromm, J.E., Scientific American, vol. 212, No. 3, pp 104-110.
- (2)
- ``Nodes, Modes and Flow Codes'', Karniadakis, G.E. and Orszag, S.A., Physics Today, March 1993, pp 34-42.
- (3)
- G. Batchelor's book: Derivation of the Navier-Stokes Equations and Conservation Laws
- (4)
- P-L. Lions, Mathematical Topics in Fluid Mechanics, Oxford Science Publications, 1996.
- (5)
- P. Constantin and C. Foias, Navier-Stokes Equations, University of Chicago Press, 1988.
- (6)
- V.A. Solonnikov and A.V. Kazhmikov, ``Existence theorems for the equations of a compressible viscous fluid,'' Ann. Rev. Fluid Mech., vol. 13, p. 79, 1982.
![\begin{displaymath}\left [ \begin{array}{llll}
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\end{array}\right ]\end{displaymath}](img7.gif)
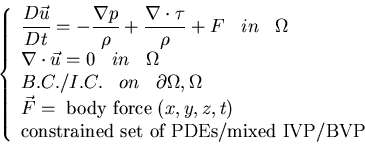
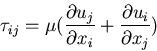
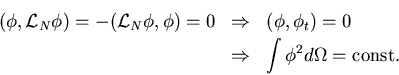
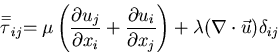
![\begin{displaymath}\stackrel{=}{\tau}_{ij} = \mu \left[ \left (\frac{\partial u_...
...ight ) - \frac{2}{3} (\nabla \cdot \vec{u}) \delta_{ij}\right ]\end{displaymath}](img38.gif)
![\begin{displaymath}\lambda \left \{ \frac{\partial \tau^p}{\partial t} + \vec{u}...
...}\right \} = \mu_{p}
[ \nabla \vec{u} + \nabla^{T} \vec{u}],\end{displaymath}](img44.gif)
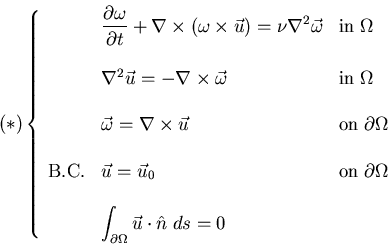
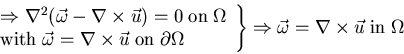
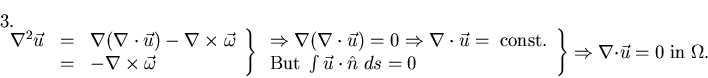
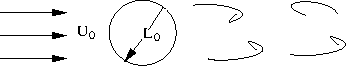
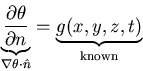
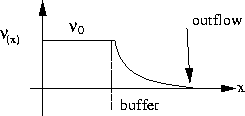
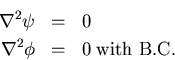
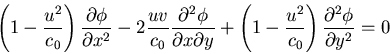
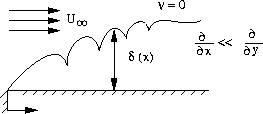
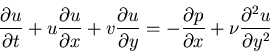
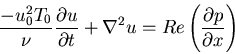
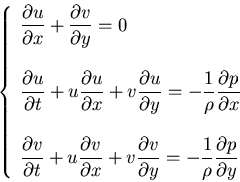
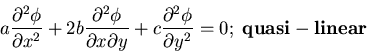
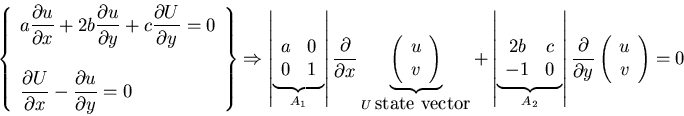
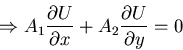
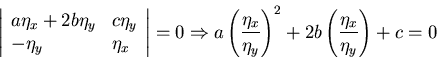


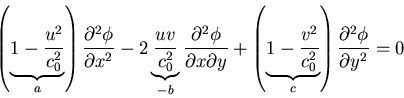
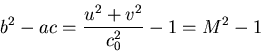
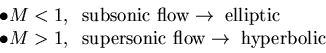
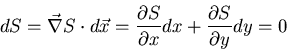
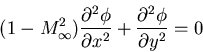
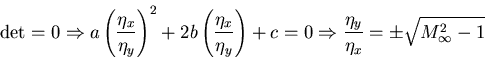
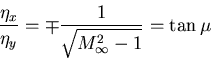
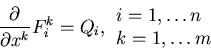
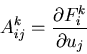
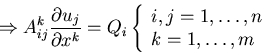
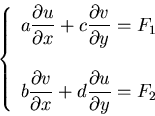
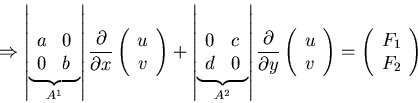
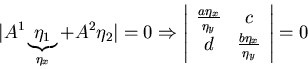
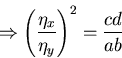
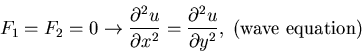
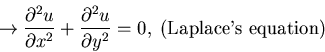
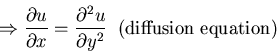
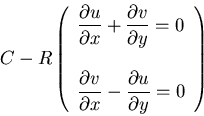
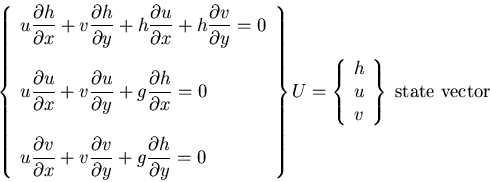
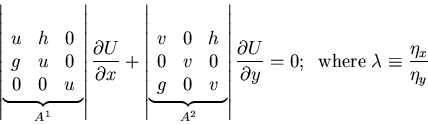
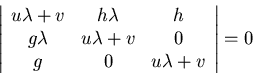
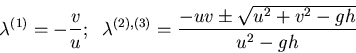
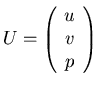 then
then
![\begin{displaymath}\left [ \begin{array}{ccc}
u & 0 & 1/\rho\\ 0 & u & 0\\ 1 &0...
... 0 & 1 & 0\end{array}\right ] \frac{\partial U}{\partial y} = 0\end{displaymath}](img190.gif)
![\begin{displaymath}\det \left [ \begin{array}{ccc} u + v \lambda & 0 & 1/\rho\\ ...
...ambda & \lambda/\rho\\
1 & \lambda & 0\end{array}\right ] = 0\end{displaymath}](img191.gif)
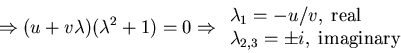
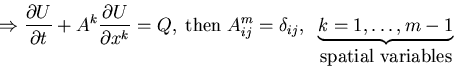
![\begin{displaymath}\det [\eta_{t} + \underbrace{A^{k}\eta_{k}}_{K_{ij}}]=0\end{displaymath}](img194.gif)